全连接、卷积网络优化 + MobilenetV2网络复现+小项目

原创已于 2024-07-05 17:55:16 修改 · 1.1k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#dnn #cnn #人工智能

于 2024-07-05 17:38:23 首次发布

首先，我们得清楚，为什么要对网络进行优化？这是基于什么样的场景下才需要考虑到的工作。

其次，需要知道，网络优化具体应该怎么做。

模型优化的目的：为了解决深度学习中的容易遇到的过拟合、梯度爆炸、梯度消失，三类问题，提出的解决办法。

一、过拟合（overfitting）

模型在训练集上的表现非常好，但是在测试集上的表现很差。通常是由于网络的参数量太大而任务本身难度太小、数据量小，导致模型相对比任务本身来说，太过于聪明，出现模型过度学习到非目标特征本身的特征，使模型输入 x 和模型权重 w 产生了线性相关性，从而导致了过拟合的出现。

解决模型过拟合的办法①：模型搭建时中加入Dropout

通过使部分模型权重失活的方式，来减少模型的参数量，以此防止过拟合的出现，需要对任务难度评估和对应的模型参数搭配非常熟悉。

使用 demo如下，可以看见在0.5的权重失活下，有0.5范围左右的输出变为了0，且失活目标位是随机的。

import torch
from torch import nn


x = torch.randn(1,1,2,10)
dropout = nn.Dropout(0.5)
out = dropout(x)
print(out)

第一次运行输出：

tensor([[[[ 0.0000, -1.1751, -1.0928, -0.6260, 0.0000, -0.0000, -0.0000,
-0.0000, 0.0000, -0.0000],
[-0.0000, 2.9594, -2.7653, -0.0000, -2.6314, 0.0000, -0.0000,
-0.0000, -3.9002, -0.0000]]]])

第二次运行输出：

tensor([[[[ 1.2695, -2.5052, 0.0000, -0.0000, -1.9676, 0.0000, 0.0483,
-0.0000, 4.4935, -2.6391],
[ 0.0000, -0.0000, 4.3747, -4.0744, 0.5882, 0.0000, 0.0000,
-0.0000, -0.5639, 0.3098]]]])
可以看见，两次输出的结果失活目标存在变化，证实了Drpout的失活目标是根据失活范围随机选定的。

模型搭建中如何使用Droputout, 下面提供DNN和CNN的demo：

import torch
from torch import nn


class DnnNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.Linear_layers = nn.Sequential(
            nn.Linear(784, 512),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(512, 256),
            nn.ReLU(),
            nn.Linear(256, 10),
            nn.Dropout(0.5)
        )

    def forward(self, x):
        h = self.Linear_layers(x)
        return h


class CnnNet(nn.Module):
    def __init__(self):
        super().__init__()

        self.conv2d_layers = nn.Sequential(
            nn.Conv2d(3, 3, 3),
            nn.ReLU(),
            nn.Dropout2d(0.5),
            nn.Conv2d(3, 3, 3),
            nn.ReLU(),
            nn.Dropout2d(0.5),
            nn.Conv2d(3, 3, 3),
            nn.Dropout2d(0.5)
        )

    def forward(self, x):
        h = self.conv2d_layers(x)
        return h


if __name__ == '__main__':
    x1 = torch.randn(1, 28*28)
    net = DnnNet()
    y1 = net(x1)
    print("y1.shape: ", y1.shape)
    print("y1: ", y1)

    x2 = torch.randn(1, 3, 10, 10)
    net = CnnNet()
    y2 = net(x2)
    print("y2.shape: ", y2.shape)
    print("y2: ", y2)

注意：卷积使用的是：nn.Dropout2d() 而全连接使用的是： nn.Dropout()

输出结果如下：

y1.shape: torch.Size([1, 3, 10])
y1: tensor([[[ 0.0000, 0.1649, -0.0000, -0.0653, -0.0000, -0.0000, 0.0000,
-0.0000, 0.0709, 0.0000],
[ 0.0000, 0.0000, -0.1149, 0.0885, 0.0980, -0.0000, 0.0000,
-0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, -0.0494, 0.2310, -0.0000, 0.0000,
-0.4139, -0.4306, 0.3792]]], grad_fn=<MulBackward0>)
y2.shape: torch.Size([1, 3, 4, 4])
y2: tensor([[[[-0.3224, -0.3224, -0.3224, -0.3224],
[-0.3224, -0.3224, -0.3224, -0.3224],
[-0.3224, -0.3224, -0.3224, -0.3224],
[-0.3224, -0.3224, -0.3224, -0.3224]],

[[ 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000],
[ 0.0000, 0.0000, 0.0000, 0.0000]],

[[ 0.1046, 0.1046, 0.1046, 0.1046],
[ 0.1046, 0.1046, 0.1046, 0.1046],
[ 0.1046, 0.1046, 0.1046, 0.1046],
[ 0.1046, 0.1046, 0.1046, 0.1046]]]], grad_fn=<MulBackward0>)

解决模型过拟合的办法②：正则化

L1正则化：会直接把数据压到0上，更多用在模型的稀疏化处理，模型过于复杂，需要减小时使用。

L2正则化：L2正则化可以将数据限制到无限接近0的位置，但是并不会等于0

总结：如果是为了防止过拟合，就用L2，希望把W变小，减弱模型的学习能力就行了，但是不希望变成0，变成0，会导致模型的退化，Relu激活函数的缺陷就是，会把结果变为0.

如何给模型添加正则化？在模型的优化器中已经加入了正则化参数，如下：

from torchvision import models
import torch

m = models.inception_v3()
opt = torch.optim.Adam(m.parameters(), weight_decay=0.2)

print("torch.optim.Adam(weight_decay=0.2): ", opt)

默认使用L2正则化，默认给了一个值是0，可以给0-1之间的值 ,而在0 - 1之间的原因是：

1. 数值稳定性：过大的 weight_decay 值可能会导致数值不稳定或权重过快减小，从而影响模型训练的效果。小的 weight_decay 值能够平滑地调整权重，避免剧烈的权重变化。

2. 正则化效果：weight_decay 值过大可能会过度惩罚权重，使得模型的表达能力降低，导致欠拟合。适中的 weight_decay 值能够有效地防止过拟合，同时又不会过多地限制模型的表达能力。

3. 常见实践：在实践中，weight_decay 通常被设为一个较小的值（例如 0.0001 到 0.01），这已经证明在许多任务中能够有效地改善模型性能。

注意：测试模型的时候，一定要加net.eval()

二、梯度爆炸

链式法则：两个函数组合起来的复合函数，导数等于里面函数代入外函数值的导乘以里面函数之导数。

由于链式法则在计算梯度时的影响，在神经网络的层数较多时，意味着连乘越多，因此很容易导致其中某一个比较大的值在连乘过程中被快速放大，导致模型出现了梯度爆炸，也就是超出了计算机所能支持的最大计算精度。

解决梯度爆炸的办法：

BatchNomal：批归一化

在模型中加入BatchNomal的作用：

1.计算时压力就不会太大，就不容易精度溢出。

2.用sigmold举例，如果数据做了归一化在激活的时候，数据很容易落在梯度比较大的区间，增大学习梯度。

3.我们希望模型的输入、w、输出的h，都能在 -1 - 1之间，这样自始至终，计算都不会太大或太小，有利于计算机计算，且网络也会学的又快又好。

4.凸显数据的差异性，提升特征提取能力，加速学习。

5.可以解决梯度爆炸，梯度爆炸：是由于梯度过大导致的，为了保证不容易出现梯度消失和梯度爆炸，首先就是把梯度限定到某个范围之间，这个范围就是-1 - 1之间。因为把每一层的特征都抑制在了-1 - 1之间，权重初始化的时候也被限制在一定范围内，x和w都被限制到类似于做了归一化的分布中，得到的结果h就不会大，反向求导的梯度就不会大。因为BachNomal是把大的分布抑制在-1 - 1之间，有可能会出0，因此就会出现梯度消失，因此，BachNomal不会解决梯度消失。全连接或者卷积，推荐每一层网络都加上BachNomal。

注意：如果加了BachNomal，最好将网络中的bias设置为False，因为BachNomal中带了滑动系数，如果网络再进行偏移，有可能偏移会过大了。
模型设计中使用BatchNomal的demo如下：

import torch
from torch import nn


class DnnNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.Linear_layers = nn.Sequential(
            nn.Linear(784, 512),
            nn.BatchNorm1d(512),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(512, 256),
            nn.BatchNorm1d(256),
            nn.ReLU(),
            nn.Linear(256, 10),
            nn.BatchNorm1d(10),
            nn.Dropout(0.5)
        )

    def forward(self, x):
        h = self.Linear_layers(x)
        return h


class CnnNet(nn.Module):
    def __init__(self):
        super().__init__()

        self.conv2d_layers = nn.Sequential(
            nn.Conv2d(3, 16, 3),
            nn.BatchNorm2d(16),
            nn.ReLU(),
            nn.Dropout2d(0.5),
            nn.Conv2d(16, 32, 3),
            nn.BatchNorm2d(32),
            nn.ReLU(),
            nn.Dropout2d(0.5),
            nn.Conv2d(32, 64, 3),
            nn.BatchNorm2d(64),
            nn.ReLU(),
            nn.Dropout2d(0.5)
        )

    def forward(self, x):
        h = self.conv2d_layers(x)
        return h


if __name__ == '__main__':
    x1 = torch.randn(3, 784)
    net = DnnNet()

    y1 = net(x1)
    print("y1.shape: ", y1.shape)
    print("y1: ", y1)

    x2 = torch.randn(1, 3, 10, 10)
    net = CnnNet()
    y2 = net(x2)
    print("y2.shape: ", y2.shape)
    print("y2: ", y2)

三、梯度消失

链式法则：两个函数组合起来的复合函数，导数等于里面函数代入外函数值的导乘以里面函数之导数。

由于链式法则在计算梯度时的影响，在神经网络的层数较多时，意味着连乘越多，因此很容易导致其中某一个比较小的值在连乘过程中被快速缩小，直至变为0，从而导致模型出现了梯度爆炸，也就是超出了计算机所能支持的最小计算精度。

抑制梯度消失的方法：

1.从激活函数角度出发，不要用sigold和tanh，用ReLU和PReLU也可以延缓

2.模型中加BachNomal一定程度上也可以抑制梯度消失,因为缩小的没有那么快了

解决梯度爆炸的办法：

只有给模型加残差，将链式法则由原本的连乘变为连加，确保权重不会等于0.

残差网络：

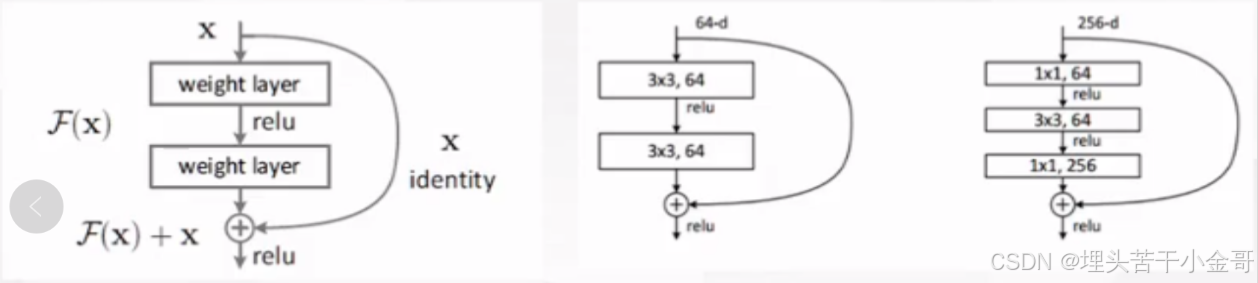
resnet18复现代码

import torch
from torch import nn


class ResBlock(nn.Module):
    def __init__(self, in_c):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Conv2d(in_c, in_c, 3, 1, padding=1, bias=False),
            nn.BatchNorm2d(in_c),
            nn.ReLU(),
            nn.Conv2d(in_c, in_c, 3, 1, padding=1, bias=False),
            nn.BatchNorm2d(in_c)
        )

    def forward(self, x):
        return self.layers(x) + x


class down_sample(nn.Module):
    def __init__(self, in_c):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Conv2d(in_c, 2 * in_c, 3, 2, padding=1, bias=False),
            nn.BatchNorm2d(2 * in_c),
            nn.ReLU()
        )

    def forward(self, x):
        return self.layers(x)


class resNet18(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Sequential(
            nn.Conv2d(3, 64, kernel_size=7, stride=2, padding=3, bias=False),
            nn.BatchNorm2d(64),
            nn.ReLU(),
            nn.MaxPool2d(3, 2, 1)
        )
        self.hidden_layer = nn.Sequential(
            ResBlock(64),
            ResBlock(64),
            down_sample(64),
            ResBlock(128),
            ResBlock(128),
            down_sample(128),
            ResBlock(256),
            ResBlock(256),
            down_sample(256),
            ResBlock(512),
            ResBlock(512)
        )

    def forward(self, x):
        return self.hidden_layer(self.conv1(x))


if __name__ == '__main__':
    net = resNet18()
    x = torch.randn(1,3,224, 224)
    y = net(x)
    print(y.shape)

resnet34复现代码：

from torch import nn
import torch


class ResBlock(nn.Module):
    def __init__(self, in_c):
        super().__init__()
        self.layer = nn.Sequential(
            nn.Conv2d(in_c, in_c, 3, 1, padding=1, bias=False),
            nn.BatchNorm2d(in_c),
            nn.ReLU(),
            nn.Conv2d(in_c, in_c, 3, 1, padding=1, bias=False),
            nn.BatchNorm2d(in_c)
        )

    def forward(self, x):
        return self.layer(x) + x


class down_sample(nn.Module):
    def __init__(self, in_c):
        super().__init__()
        self.layer = nn.Sequential(
            nn.Conv2d(in_c, 2 * in_c, 3, 2, padding=1, bias=False),
            nn.BatchNorm2d(2 * in_c),
            nn.ReLU()
        )

    def forward(self, x):
        return self.layer(x)


class resNet34(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Sequential(
            nn.Conv2d(3, 64, 7, 2, padding=3, bias=False),
            nn.BatchNorm2d(64),
            nn.ReLU()
        )
        self.hidden_layer = nn.Sequential(
            ResBlock(64),
            ResBlock(64),
            ResBlock(64),
            down_sample(64),
            ResBlock(128),
            ResBlock(128),
            ResBlock(128),
            ResBlock(128),
            down_sample(128),
            ResBlock(256),
            ResBlock(256),
            ResBlock(256),
            ResBlock(256),
            ResBlock(256),
            ResBlock(256),
            down_sample(256),
            ResBlock(512),
            ResBlock(512),
            ResBlock(512),
        )

    def forward(self, x):
        print(self.conv1(x).shape)
        return self.hidden_layer(self.conv1(x))


if __name__ == '__main__':
    net = resNet34()
    x = torch.randn(1,3,228,228)
    y = net(x)
    print(y.shape)

总结：基于以上，结合Dropout 、 BatchNomal 、残差三种方式，就可以完美的避免模型搭建经常遇到的三类问题，过拟合、梯度爆炸、梯度消失。

网络优化技巧：

1*1 和 3*3 的卷积对比：

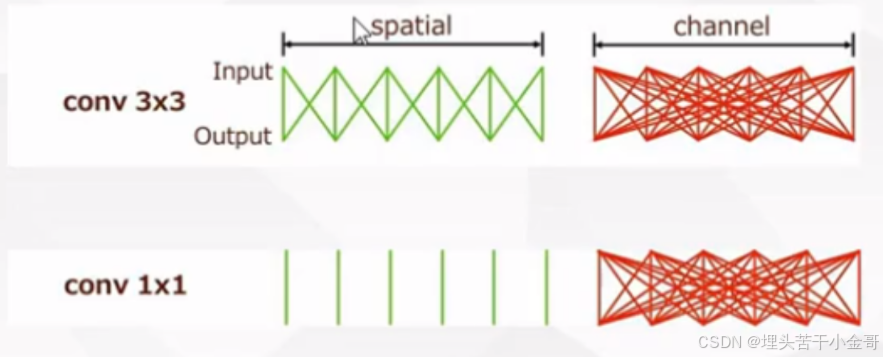
可以发现，1*1的卷积并不会做像素融合

分离卷积：

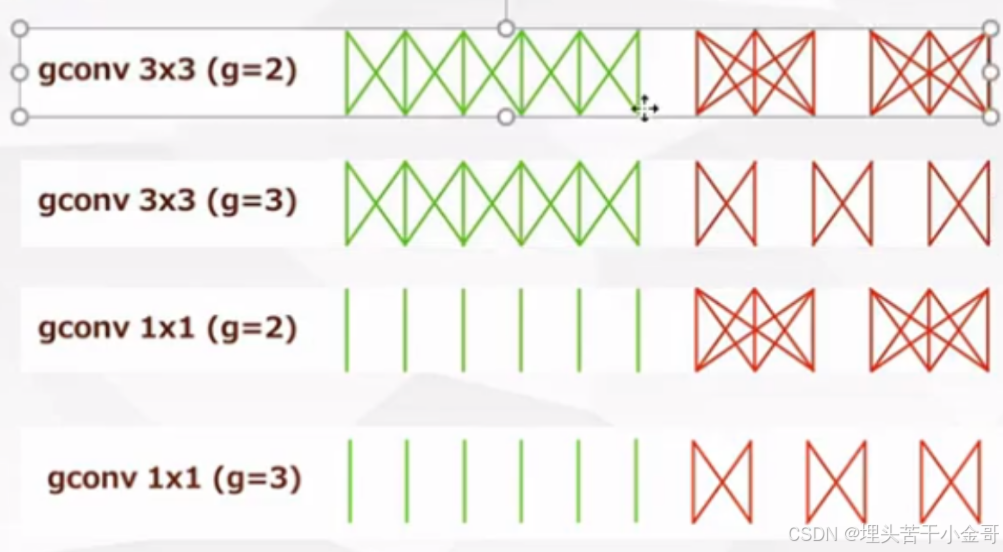
分离卷积的前提：

1.组数需要能被输入和输出通道整除
2.卷积至少要保证存在通道融合，否则通道完全分离，拿到的特征是十分片面的。

深度可分离卷积：输入通道，输出通道，分组，都一样

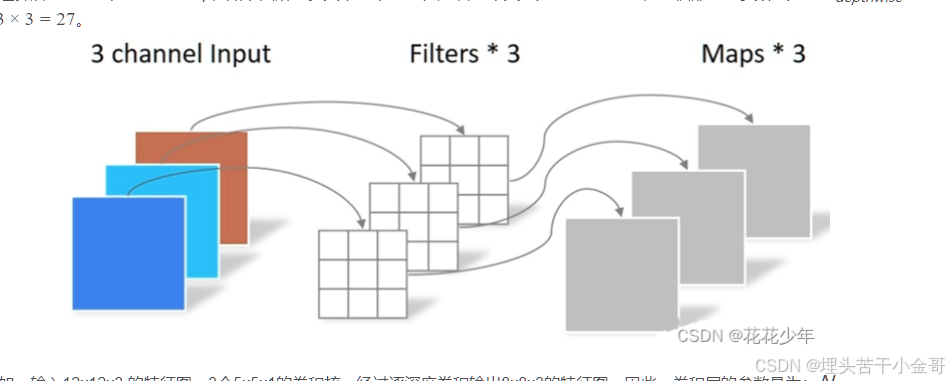
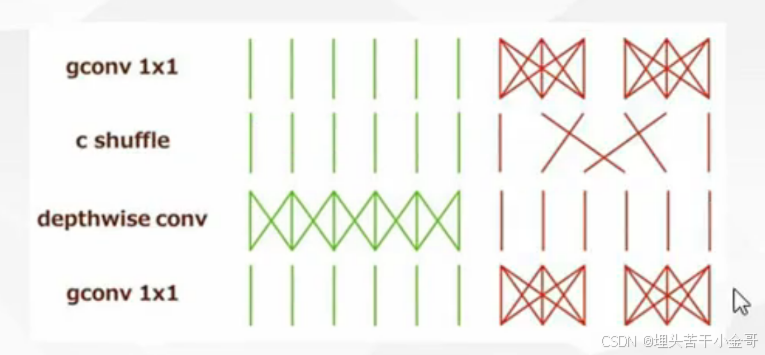
通道混洗：

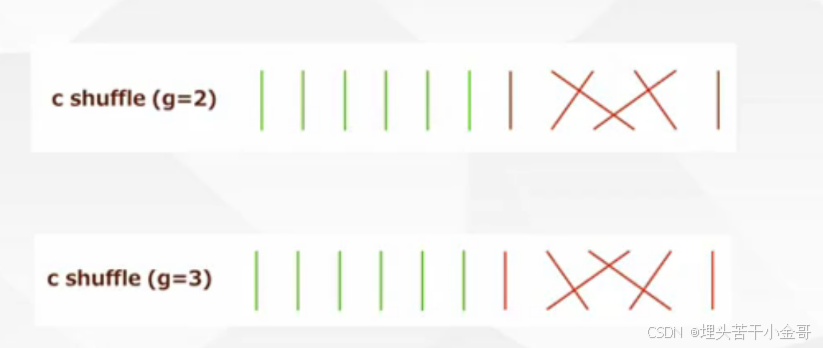
1.将通道转为深度可分离卷积，输入通道、输出通道、组数完全一一对应
2.交叉的方法：①神经网络 ②reshape，一般第二种比较多，因为1*1的卷积也会有一个学习的过程，而通道混洗，只是为了改变位置，而不是特征本身，因此，reshape更合适。

高效的网络模块：

ResNet瓶颈结构：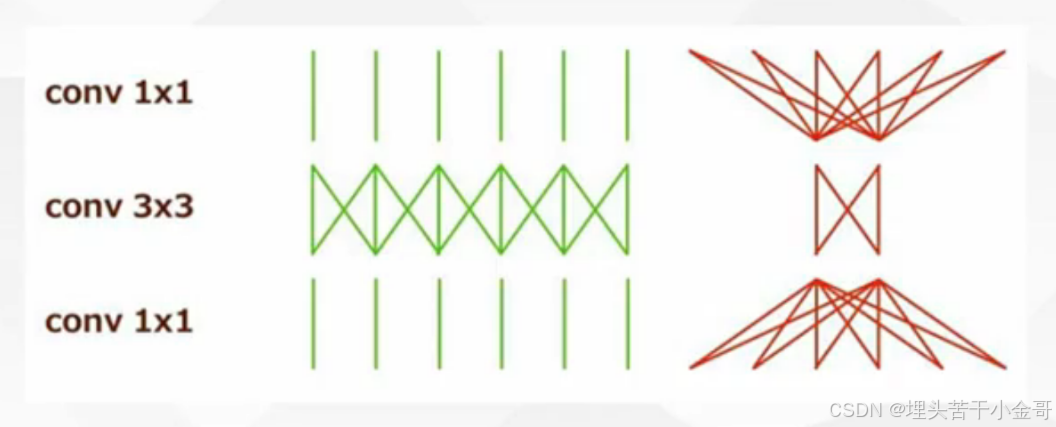

MobilenetV1：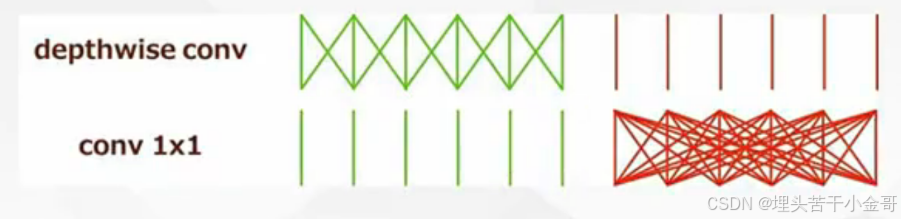

MobilenetV2：

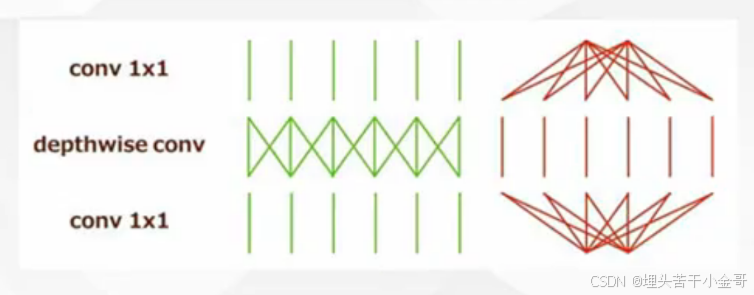
ShuffleNet：

下面附上MobilenetV2的复现代码：

import torch
from torch import nn


config = [
    [-1, 32, 1, 2],
    [1, 16, 1, 1],
    [6, 24, 2, 2],
    [6, 32, 3, 2],
    [6, 64, 4, 2],
    [6, 96, 3, 1],
    [6, 160, 3, 2],
    [6, 320, 1, 1]
]


class Block(nn.Module):
    def __init__(self, p_c, i, t, c, n, s):  # i代表当前第几个block
        super().__init__()
        # 每个重复的最后一次负责下采样
        # 所以i = n-1 的时候进行操作
        self.i = i
        self.n = n

        _s = s if i == n-1 else 1  # 判断是否是最后一次重复的步长，是最后一次重复的步长为2
        # 判断是否是最后一次重复，最后一次重复负责通道变换为下一层的输入
        _c = c if i == n-1 else p_c

        _p_c = p_c * t  # 输入通道扩增倍数

        self.layer = nn.Sequential(
            nn.Conv2d(p_c, _p_c, 1, 1, bias=False),
            nn.BatchNorm2d(_p_c),
            nn.ReLU6(),
            nn.Conv2d(_p_c, _p_c, 3, _s, padding=1, groups=_p_c, bias=False),
            nn.BatchNorm2d(_p_c),
            nn.ReLU6(),
            nn.Conv2d(_p_c, _c, 1, 1, bias=False),
            nn.BatchNorm2d(_c)
        )

    def forward(self, x):
        if self.i == self.n-1:
            return self.layer(x)
        else:
            return self.layer(x) + x


class MobilenetV2(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.input_layer = nn.Sequential(
            nn.Conv2d(3, 32, 3, 2, padding=1, bias=False),
            nn.BatchNorm2d(32),
            nn.ReLU6()
        )
        self.blocks = []
        p_c = config[0][1]
        for t, c, n, s in config[1:]:
            for i in range(n):
                self.blocks.append(Block(p_c, i, t, c, n, s))
            p_c = c

        self.hidden_layer = nn.Sequential(*self.blocks)

        self.output_layer = nn.Sequential(
            nn.Conv2d(320, 1280, 1, 1, bias=False),
            nn.BatchNorm2d(1280),
            nn.ReLU6(),
            nn.AvgPool2d(7, 1),
            nn.Conv2d(1280, 10, 1, 1, bias=False)
        )

    def forward(self, x):
        h = self.input_layer(x)
        print(h.shape)
        h = self.hidden_layer(h)
        print(h.shape)
        h = self.output_layer(h)
        h = h.reshape(-1, 10)
        return h


if __name__ == '__main__':
    net = MobilenetV2(config)
    x = torch.randn(1,3, 224, 224)
    y = net(x)
    print(y.shape)

还差使用复现的MobileNet网络实现小项目的训练、测试代码，后面抽空补上～