神经网络与深度学习第二次课程总结

一．误差反传算法

BP（backpropagation反向传播）算法  

网络结构与符号定义

设网络层数共L层，输入层为0层，输出层为L层，层数用上标[l]表示

网络中第l层输出:a[l] =f(z[l])，其中z[l]为该层线性输出，若选取作用函数为Sigmoid函数，则可记为:：a[l]= σ(z[l])

第l层的第i个节点线性输出为：zi[l]=∑wij[l]*aj[l-1]

网络中第l层线性输出: z[l]=W[l]*a[l-1]，

其中W为权值矩阵，列数为上层神经元数目，行数为本层神经元数目。

BP算法基本思想

设算法的输入输出样本(导师信号)为:{x(1),y(1)}, {x(2), y(2)}......共N个样本。

网络训练的目的就是使对每一个输入样本，调整网络权值参数W，使输出均方误差最小化。这是一个最优化问题。指标函数:

J(x,w)=1/2*(e(i)(x,w))2

其中e(i)= y(i)-y^(i)

算法的实现流程为

  1. 前向传播：输入数据逐层计算，得到预测输出 。

  2. 误差计算：使用均方误差损失函数 。

  3. 反向传播：从输出层到输入层逐层计算梯度，利用链式法则更新权值。

  4. 梯度下降：权值更新公式为 ，其中α为学习率。

计算过程

1.初始化：从输出层（l=L）开始计算误差。

2.输出层梯度：

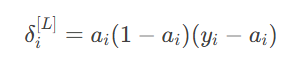
3.隐含层梯度：

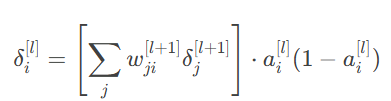
4.权值更新：

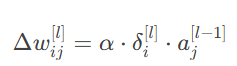
5.迭代更新：从输出层逐层反向更新至输入层。

二．性能优化

常用技巧

模型初始化：

把所有权值在[-1,1]区间内按均值或高斯分布进行初始化。

Xavier初始化：为了使得网络中信息更好的流动，每一层输出的方差应该尽量相等。因此需要实现下面的均匀分布：

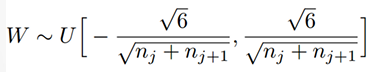
训练数据的分布：

训练数据，验证数据，测试数据通常按70%，15%，15%或60，20，20分布，数据很多时，训练和验证数据可适当减少。

另外，可以采用K折交叉验证法，把原始训练数据被分成K个不重叠的子集。 然后执行K次模型训练和验证，每次在K−1个子集上进行训练，并在剩余的一个子集（在该轮中没有用于训练的子集）上进行验证。最后，通过对 𝐾次实验的结果取平均来估计训练和验证误差。

权重衰减:

为防止过拟合和权值震荡，加入新的指标函数项：

第二项约束了权值不能过大。在梯度下降时，导数容易计算：

动量法：

用于处理病态曲率问题，下面是病态曲率问题的形象解释：

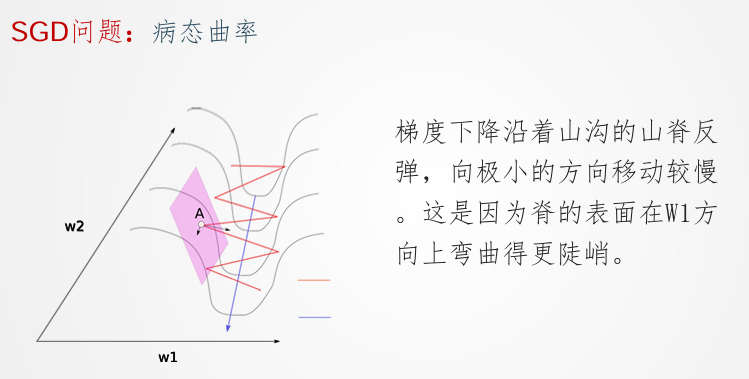
动量方法相当于把纸团换成了铁球；不容易受到外力的干扰，轨迹更加稳定；同时因为在鞍点处因为惯性的作用，更有可能离开平地，到达极小值点，避免了陷入局部极小值解。

更新公式为：

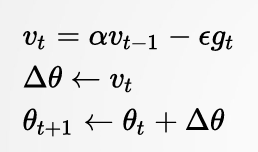
自适应梯度方法：

即权值参数自适应变化，具有较大偏导的参数相应有一个较大的学习率，而具有小偏导的参数则对应一个较小的学习率。通过自适应调节学习速率，可以加速收敛。

三．卷积神经网络基础

全连接网络的问题：

全连接网络存在着参数爆炸、容易过拟合和局部极小值的问题。

输入为图像时（如 1000×1000），隐含层节点数过多（如 1M），导致参数数量级达1012，计算效率低且难收敛。通过改用局部连接网络（如卷积层），可以减少参数数量。

另外，权值过多易过拟合，优化过程易陷入局部极小值，可以对信息分层处理，每一层在上层提取特征的基础上获取进行再处理，得到更高级别的特征。

深度学习平台简介：

主流框架有TensorFlow、PyTorch、Caffe、MXNet 等，课程中主要使用pytorch

张量（Tensor）与计算图是pytorch中的核心概念。在计算图中，用“结点”（nodes）和“线”(edges)的有向图来描述数学计算的图像。“节点”用来表示施加的数学操作，但也可以表示数据输入的起点/输出的终点，或者是读取/写入持久变量的终点。“线”表示“节点”之间的输入/输出关系。这些数据“线”可以输运“size可动态调整”的多维数据数组，即“张量”（tensor）。

Pytorch中使用 tensor 表示数据，用 Dataset、DataLoader 读取样本数据和标签，用变量(Variable) 存储神经网络权值等参数，用计算图 (computational graph) 来表示计算任务，在代码运行过程中同时执行计算图。

卷积神经网络基础

1.核心概念：

卷积操作：局部连接、权值共享、多通道卷积（如 RGB 三通道）。

填充（Padding）与步长（Stride）：控制输出尺寸与信息保留。

池化（Pooling）：降维并提取局部统计特征（均值或最大值）。

2.网络结构

由卷积层、池化层交替堆叠，后接全连接层。

前向传播公式为：

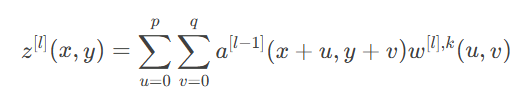
反向传播：推导了池化层与卷积层的误差回传机制。

3.典型任务：图像分类、目标检测、语义分割等，常用数据集包括 MNIST、CIFAR、ImageNet。

LeNet5网络

1.网络结构

层级设计：

输入层（32×32）→ 卷积层（C1: 6@28×28）→ 池化层（S2: 6@14×14）

→ 卷积层（C3: 16@10×10）→ 池化层（S4: 16@5×5）→ 全连接层（C5: 120 → F6: 84 → 输出层: 10）。

参数计算：

C1 层：6 个 5×5 卷积核，共 (5×5+1)×6×28×28=122,304 个连接。

输出层：使用径向基函数（RBF）计算类别距离。

2.代码实现

PyTorch 实现示例：通过 nn.Sequential 构建网络，包含卷积、池化、激活函数（Sigmoid）、全连接层。

LeNet5网络的特点为：无填充（Padding）、平均池化、浅层结构（约 6 万参数）。

与现网区别主要为：早期网络未使用 ReLU、最大池化或批量归一化，层数较浅。