神经网络与深度学习第一次课程总结

神经网络定义与发展

人工神经网络或简称神经网络(NN)，是从微观结构与功能上模拟人脑神经系统而建立的一类模型，是模拟人的智能的一条途径。神经网络主要经历了如下的6个发展过程

1.创始：

 1943年， McCulloch和W.Pitts，提出NN数学模型；

 1949年， Hebb规则

2.初步发展：

 1958年， Rosenblatt 感知机和联想学习

 1960年， Widrow和Hoff ADALINE学习算法

3.停滞期： 1969年 Minsky “Perceptron” XOR问题

4.复兴期(二十世纪八、九十年代)：

 1982 Hopfield解决TSP问题

 1986 Rumelhart和McClelland BP

 新型神经网络提出，如RBFN, Hopfield网络， Boltzmann机等

5. 爆发期(2006~2021年)：

 2006年： Hinton提出深度学习

 应用的爆发式发展：语音识别：微软， 2011； ImageNet: Google, 2011-；

AlphaGo: DeepMind, 2016

6. 通用人工智能(2021起)：以Transformer和ChatGPT 3.5为标志

2022年新兴技术趋势确定了25种需要了解的新兴技术，主要包含三个主题：沉浸式体验的演进、加速人工智能自动化和优化技术人才交付。

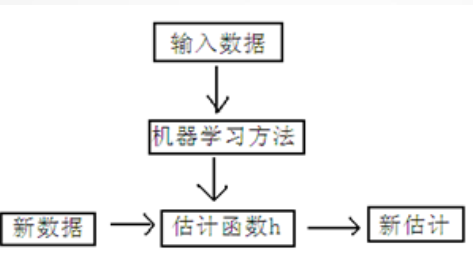
神经网络的应用

数据基础，算法引擎和计算平台奠定了人工智能崛起的三大基石，计算机视觉，机器学习，图像识别，语言识别，机器人，自然语言处理是人工智能发展的6大关键技术。

线性回归

定义： 利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，

线性回归的要素为：训练集x，输出数据y，拟合的函数（模型）和训练数据的条目数

最常见的线性回归问题是一维直线拟合，对其进行扩展，假设和n个元素有关，，则有

假设给定样本(xi,yi), 构造代价(误差、损失)函数：

求解多维线性回归问题，就是要找到超平面参数𝛉，使𝐽(𝛉)最小，即求解min𝐽(𝛉)

求解，能够得到

线性二分类问题

定义： 线性分类器则透过特征的线性组合来做出分类决定，以达到此种目的。简言之就是样本通过直线(或超平面)可分。此处特地强调一下线性分类与线性回归差别：

输出意义不同：属于某类的概率<->回归具体值

参数意义不同：最佳分类直线<->最佳拟合直线

维度不同：前面的例子中，一个是一维的回归，一个是二维的分类

使用sigmod函数来描述将线性输出映射到概率

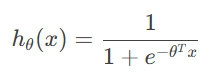
交叉熵损失函数为

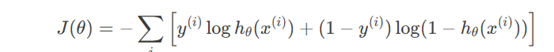
将线性分类扩展得到多分类回归：

Sigmod函数被扩展为

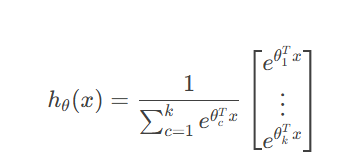
输出为类别概率分布，通过指数函数实现了概率的归一化，可以用于多分类问题。

神经元模型

1943年心理学家W.McCulloch和数学家W.Pitts合作提出了M-P神经元模型

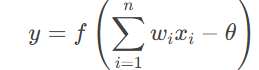
其中，作用函数f(x)主要有如下几种形式

1. 非对称型 Sigmoid 函数 (Log Sigmoid)

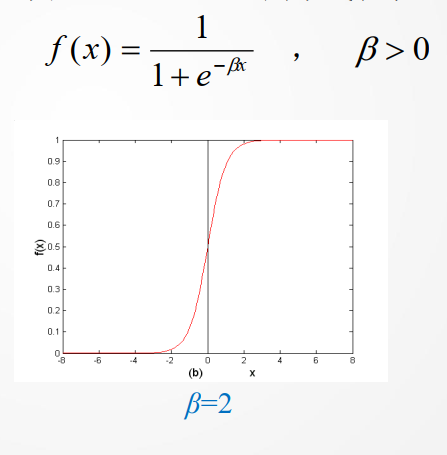
（2）对称型 Sigmoid 函数 (Tangent Sigmoid)

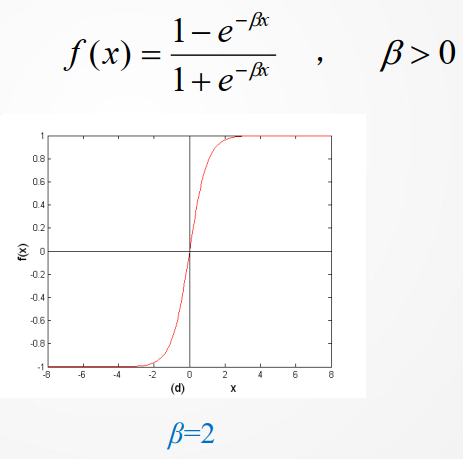
（3）.对称型阶跃函数，即具有阶跃作用函数的神经元，称为阈值逻辑单元

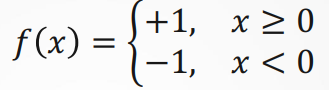
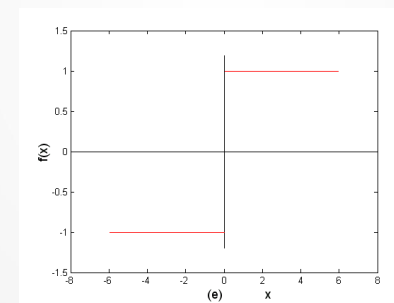
根据hebb规则，

连接权值的调整量与输入与输出的乘积成正比。

感知机模型：

感知机(Perceptron)是1957年，由Rosenblatt提出，是神经网络和支持向量机的基础，可用于解决线性分类问题。

感知机从输入到输出的模型如下：

Sign为符号函数

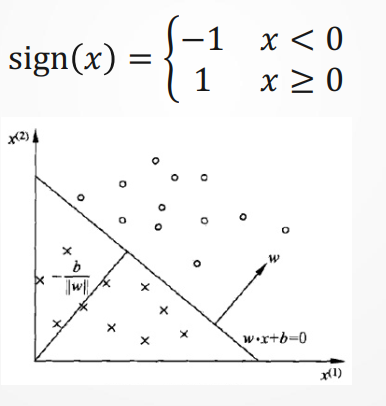
其损失函数定义为

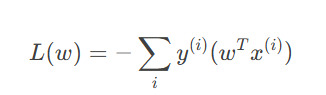
仅对误分类样本更新权值，权值的更新规则为

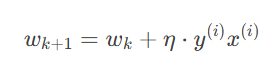
多层感知机

对于xor这类线性不可分问题，引入了多层感知机的概念。

解决方法： 使用多层感知机

• 在输入和输出层间加一或多层隐单元，构成多层感知器（多层前馈神经网络）。

• 加一层隐节点（单元）为三层网络，可解决异或（XOR）问题由输入得到两个隐节点、一个输出层节点的输出：

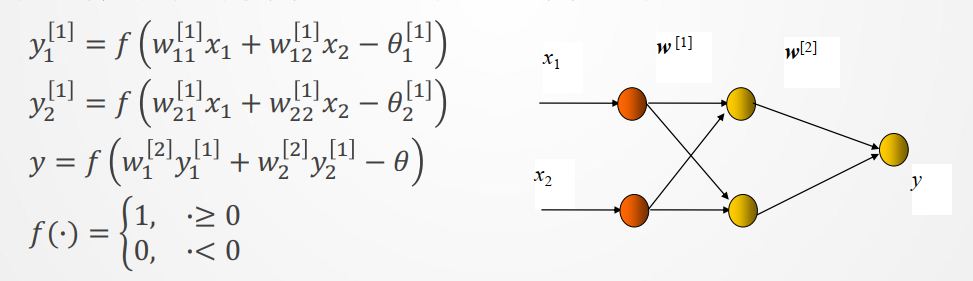
在上式中，要特别注意w角标所表示的含义。

三层感知器可识别任一凸多边形或无界的凸区域。

更多层感知器网络，可识别更为复杂的图形。

多层感知器网络，有如下定理：

定理1 若隐层节点（单元）可任意设置，用三层阈值节点的网络，可以实现任意的二值逻辑函数。

定理2 若隐层节点（单元）可任意设置，用三层S型非线性特性节点的网络，可以一致逼近紧集上的连续函数或按 范数逼近紧集上的平方可积函数。

多层前馈网络与BP算法

多层感知机是一种多层前馈网络， 由多层神经网络构成，每层网络将输出传递给下一层网络。神经元间的权值连接仅出现在相邻层之间，不出现在其他位置。如果每一个神经元都连接到上一层的所有神经元（除输入层外），则成为全连接网络。

多层前馈网络的反向传播 （BP）学习算法，简称BP算法，是有导师的学习，它是梯度下降法在多层前馈网中的应用。

网络结构： 𝐮（或𝐱 ）、 𝐲是网络的输入、输出向量，神经元用节点表示，网络由输入层、隐层和输出层节点组成，隐层可一层，也可多层（图中是单隐层），前层至后层节点通过权联接。由于用BP学习算法，所以常称BP神经网络。

BP学习算法由正向传播和反向传播组成：

① 正向传播是输入信号从输入层经隐层，传向输出层，若输出层得到了期望的输出，则学习算法结束；否则，转至反向传播。

② 反向传播是将误差(样本输出与网络输出之差）按原联接通路反向计算，由梯度下降法调整各层节点的权值和阈值，使误差减小。