Date:January 5th Title: 子集计数题解-优快云博客

文章描述了一个编程竞赛题目，要求找到满足特定条件的数组子集数量。条件是数组A中的最大值大于数组B中对应项的和。通过排序和01背包策略解决，对数组A和B进行处理，动态规划计算满足条件的子集方案数，并对结果取模以适应大数据范围。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

xjoi题解：P8084 子集计数

时间：2s 空间：512M

题目描述：

给定两个长度为n的数组A,B，求满足以下条件的1,2,…,N的非空子集S的数目：

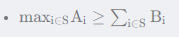
由于答案可能非常大，输出模 998244353 后的答案。

输入格式：

第一行，包含一个正整数 n，表示数组大小。

第二行包含n个整数A1,A2,...,An，表示数组A。

第三行包含n个整数B1,B2,...,Bn，表示数组B。

输出格式：

输出一行整数表示答案。

样例1输入：

3 1

1 2

样例1输出：

样例2输入：

1 1

2 2

样例2输出：

约定：

对于100%的数据，1≤n,Ai,Bi≤5000。

样例1解释：总共有 3 种非空子集，分别是 1,2,1,2，满足条件的有 1,1,2。

题意:

有长度为n的a数组和b数组，然后在同时数组内找若干项并分别相加，求a的最大值大于b的若干项的方案数。

分析：

首先我们将这a数组进行排序，方便我们找出a数组的最大值，我们在选择的过程中，当前选到ai，

ai需要大于等于b[i]加上先前选的数的总和，那么先前选的数的总和小于等于ai-bi,在满足此条件的情况下可选bi方案数，先前的bi项已经变成选和不选了，这道题变成了01背包，取得数值就是代价，用01背包求取法有多少种。

代码：

#include<bits/stdc++.h>
using namespace std;
long long dp[101010], a[101010], b[101010],ans;
long long mod=998244353;
int main() {
    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    for (int i = 1; i <= n; i++) {
        cin >> b[i];
    }
    dp[0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=a[i]-b[i];j++)
        {
            ans=(ans+dp[j])%mod;
        }
        for(int j=5000;j>=b[i];j--)
        {
            dp[j]=(dp[j]+dp[j-b[i]])%mod;
        }    
    }
    cout<<ans;
}

The End