数字图像处理-实验2-空域图像增强_图像空域增强-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_56822454/article/details/137792273

本文介绍了如何通过编程实现灰度变换（如图像变暗、变亮和降低/增加对比度）、直方图均衡化以及gamma和对数变换，展示了这些技术如何改变图像的视觉效果和动态范围，以及它们在增强图像细节方面的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

实验二空域图像增强——点运算

一、实验目的：

（1）掌握灰度变换的实现方法；

（2）理解并掌握点运算的实现方法；

（3）理解并掌握直方图均衡化的方法。

二、实验环境：

（1）实验硬件环境

笔记本电脑

（2）软件及工具包
1. Windows10操作系统，开发环境是Python3，需要配置的数学运算库包括NumPy、Matplotlib、OpenCV，编辑器是jupyter notebook。
  1. NumPy是 Python 语言的一个扩展程序库。其中提供了许多向量和矩阵操作，能轻松完成最优化、线性代数、积分、插值、特殊函数、傅里叶变换、信号处理和图像处理、常微分方程求解以及其他科学与工程中常用的计算，不仅方便易用而且效率更高。NumPy 是一个开源的Python科学计算基础库，是SciPy、Pandas等数据处理或科学计算库的基础。
    1. Matplotlib是一个Python 的2D绘图库，Matplotlib也是Python中最常用的可视化工具之一，它的功能非常强大，可以通过调用函数轻松方便地绘制数据分析中常见的各种图像，比如折线图、条形图、柱状图、散点图、饼图等。
      1. OpenCV 是一个的跨平台计算机视觉库，可以运行在 Linux、 Windows 和 Mac Os 操作系统上。它轻量级而且高效，由一系列 C 函数和少量 C++ 构成，同时也提供了 python 接口，实现了图像处理和计算机视觉方面的很多通用算法。

三、实验内容

1.编程实现图像的灰度变换，包括图像变暗、图像变亮和降低对比度。提示：可通过全局线性变换实现；

2.编程实现图像的直方图均衡化。提示：可通过调用OpenCV工具包中的equalizeHist()函数实现；

3.编程实现gamma变换。

四、实验程序及运行结果

（1）实验代码：

import numpy as np 
import matplotlib.pyplot as plt
import cv2 as cv
def show(img):
    if img.ndim == 2:
        plt.imshow(img,cmap='gray',vmin=0,vmax=255)
    else:
        plt.imshow(cv.cvtColor(img, cv.COLOR_BGR2RGB))
    plt.show()
#全局灰度线性变换
def global_linear_transmation(img,c=0,d=255):
   # img=im.copy() #c=0,d=255将灰度范围设为0~255
    maxV=img.max()
    minV=img.min()
    if maxV==minV:#最大灰度值=最小灰度值时返回原图像
        return np.uint8(img)
    for i in range(img.shape[0]):
            for j in range(img.shape[1]):
                img[i,j] = ((d-c)/(maxV-minV))*(img[i,j]-minV)+c
    return np.uint8(img)

统计灰度值函数、显示原图像和单通道灰度值像素个数统计代码：

#统计各灰度值的像素个数
def histogram(image):
    (row, col) = image.shape
    hist = [0]*256
    for i in range(row):
        for j in range(col):
            hist[image[i,j]] +=1#遍历图片中每一点的像素值并统计
    return hist
img = cv.imread('iris.jpg')#显示原图像
show(img)
img_hist = histogram(img[:,:,2])
plt.bar(range(256),img_hist)

图像变暗、图像变亮和降低对比度代码：

img = cv.imread('iris.jpg')
img_t = img#图像变暗
img_t[:,:,0] = global_linear_transmation(img_t[:,:,0],c=5,d=190)
img_t[:,:,1] = global_linear_transmation(img_t[:,:,1],c=10,d=150)
img_t[:,:,2] = global_linear_transmation(img_t[:,:,2],c=25,d=130)
show(img_t)
img_hist_t = histogram(img_t[:,:,0])
plt.bar(range(256),img_hist_t)
img = cv.imread('iris.jpg')
img_t1 = img#图像变亮
img_t1[:,:,0] = global_linear_transmation(img_t1[:,:,0],c=35,d=255)
img_t1[:,:,1] = global_linear_transmation(img_t1[:,:,1],c=40,d=255)
img_t1[:,:,2] = global_linear_transmation(img_t1[:,:,2],c=45,d=255)
#show(np.hstack([img,img_t1]))
show(img_t1)
img_hist_t1 = histogram(img_t1[:,:,2])
plt.bar(range(256),img_hist_t1)
img = cv.imread('iris.jpg')
img_t2 = img#降低对比度
img_t2[:,:,0] = global_linear_transmation(img_t2[:,:,0],c=40,d=230)
img_t2[:,:,1] = global_linear_transmation(img_t2[:,:,1],c=45,d=170)
img_t2[:,:,2] = global_linear_transmation(img_t2[:,:,2],c=50,d=160)
show(img_t2)
img_hist2 = histogram(img_t2[:,:,2])
plt.bar(range(256),img_hist2)
img = cv.imread('iris.jpg')
img_t3 = img#增加对比度
img_t3[:,:,0] = global_linear_transmation(img_t3[:,:,0],c=0,d=255)
img_t3[:,:,1] = global_linear_transmation(img_t3[:,:,1],c=-10,d=255)
img_t3[:,:,2] = global_linear_transmation(img_t3[:,:,2],c=-5,d=255)
show(img_t3)
img_hist3 = histogram(img_t3[:,:,2])
plt.bar(range(256),img_hist3)

运行结果：

原图像及图像的三个通道灰度级像素值统计：

图像变暗处理后的实验结果及图像的三个通道灰度级像素值统计：

图像变亮处理后的实验结果及图像的三个通道灰度级像素值统计：

降低对比度处理后的实验结果及图像的三个通道灰度级像素值统计：

增加对比度后的实验结果：

（2）实验代码：

img = cv.imread('iris.jpg')
show(img)
img_hist = histogram(img[:,:,1])
plt.bar(range(256),img_hist)
img_e = img
img_e[:,:,0]=cv.equalizeHist(img_e[:,:,0])
img_e[:,:,1]=cv.equalizeHist(img_e[:,:,1])
img_e[:,:,2]=cv.equalizeHist(img_e[:,:,2])
show(img_e)
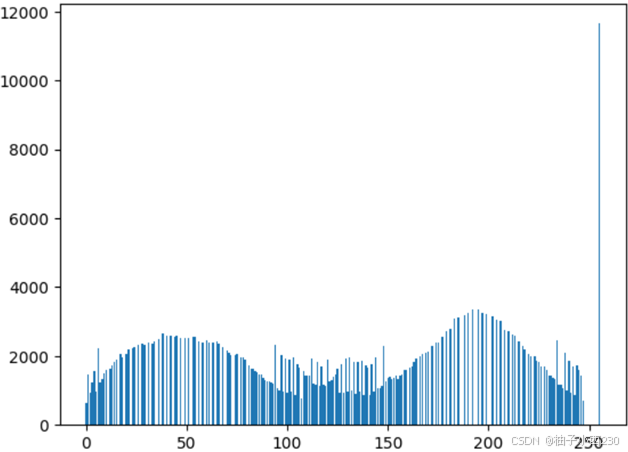
img_hist_e = histogram(img_e[:,:,2])
plt.bar(range(256),img_hist_e)

运行结果：

（3）实验代码：

def power_law_transformation(im,gamma=1,c=1):
    img = np.zeros([im.shape[0],im.shape[1]])
    for i in range(im.shape[0]):
        for j in range(im.shape[1]):
            img[i,j]=c*255.0*(im[i,j]/255.0)**gamma
    return np.uint8(img)
img = cv.imread('iris.jpg')
show(img)
img_g = img
img_g[:,:,0]=power_law_transformation(img_g[:,:,0],gamma=0.3,c=1)
img_g[:,:,1]=power_law_transformation(img_g[:,:,1],gamma=0.3,c=1)
img_g[:,:,2]=power_law_transformation(img_g[:,:,2],gamma=0.3,c=1)
show(img_g)
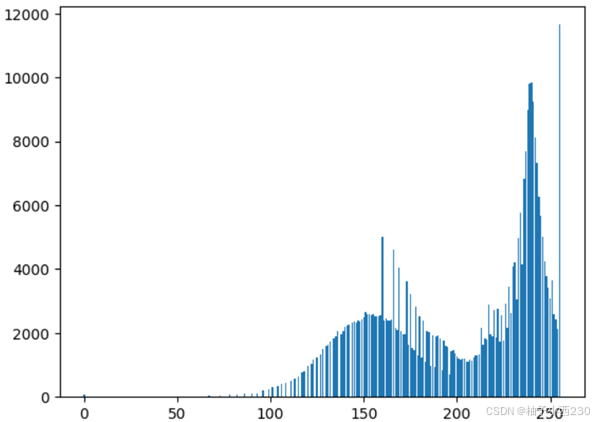
img_hist_g = histogram(img_g[:,:,2])
plt.bar(range(256),img_hist_g)

运行结果：

五、实验分析（对实验中出现的现象及遇到的问题进行分析、讨论，并对实验提出自己的建议和改进措施。）

1.通过全局线性变换实现灰度变换分析：

要将灰度范围从[a，b]更改为[c，d]，则：

$s=\left [ \frac{d-c}{b-a} \right ]\left [ r-a \right ]+c$

令系数k=(d-c)/(b-a)，则k的不同，处理后的图片效果也不同：

当0<k<1时，变换后的灰度范围会变小此时图像实际上被压缩了，图像质量会有所下降，在某些时候，需要节约存储空间可以使0<k<1；

当K=1时，图像的灰度范围没变，但是灰度区间可能发生平移；

当K>1时，图像的灰度范围变大，常常能够更凸显细节。

当K<0时，图像的灰度反转，即亮区域变成暗区域，暗部分又变成亮的部分。

本实验中的三个通道0、1、2分别对应B、G、R，图像的灰度变换包括图像变亮、变暗、对比度的增加和减小。图像的亮暗调节可以通过改变灰度值整体范围增加或减小。图像的对比度是通过灰度级范围来度量的，而灰度级范围可通过观察灰度直方图得到，灰度级范围越大代表对比度越高，反之对比度越低。最简单的一种对比度增强的方法是通过灰度值的线性变换实现的。

本实验中，我先观察原图像的三个通道的灰度直方图，然后小范围的改变灰度级，图像变暗处理就是对应的将灰度直方图的灰度级分布向左移，即灰度级范围整体减小；图像变亮处理是对应的将灰度直方图的灰度级向右移动，即灰度级范围整体增加；减小对比度就是将灰度级范围按照原图像灰度级分布趋势，向分布密集的范围缩小；增加对比度就是将原对比度进行扩展，在实验中，在选取参数值时，为了达到预期实验结果，将c的值取到了负数，目的是将没有灰度值分布的小范围灰度值加到高灰度级范围内而不影响对比度的增加。

建议及改进措施：全局线性变换的缺点在于不能很好的突出细节，灰度值的整体变化，使得原图像可能丢失重要信息。分段线性变换就能很好的解决该问题。

2.图像的直方图均衡化实验结果分析：

直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。这样就增加了像素之间灰度值差别的动态范围，从而增大对比度，使图像清晰，达到增强的目的。

从实验结果部分可以看出，均衡化后的图像对比度明显增强，观察到了更多的细节信息。尽管直方图均衡化是一种简单且有效的图像增强算法，但它也存在一些缺陷：直方图均衡化是一种全局变换方法，它将整个图像的直方图都变成了均匀分布的直方图，这可能会导致一些像素值的细节信息丢失或被模糊化。直方图均衡化的映射函数是非线性的，这意味着它会改变像素值之间的距离，从而可能导致一些图像特征的失真；

建议及改进措施：在实际应用中，直方图均衡化算法可能需要结合其他方法进行优化或改进，以克服其缺陷。例如，可以使用局部直方图均衡化等技术来改进算法的局限性。

3.Gamma变换实验结果分析：

伽马变换主要用于图像的校正，将灰度过高或者灰度过低的图片进行修正，增强对比度。变换公式就是对原图像上每一个像素值做乘积运算：

s=c*rγ

通过改变γ值的取值，我们发现γ值以1为分界，值越小，对图像低灰度部分的扩展作用就越强，值越大，对图像高灰度部分的扩展作用就越强，通过不同的γ值，就可以达到增强低灰度或高灰度部分细节的作用。伽马变换对于图像对比度偏低，并且整体亮度值偏高（对于于相机过曝）情况下的图像增强效果明显。

建议及改进措施：

在实验时，要不断改变γ值，观察实验结果，与课上老师所讲结论进行比较，而不只拘泥于课本知识，要从多个角度考虑图像变换的本质和意义，除了检验和验证课本知识的结论外还要有探索精神，探寻图像变换背后的本质问题，思考该方法可用与什么领域，解决什么问题。

六、思考题

1.模仿gamma变换的函数，编写实现对数变换的函数。

实验代码：

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
def show(img):
    if img.ndim == 2:
        plt.imshow(img, cmap='gray', vmin=0, vmax=255)
    else:
        img = cv.cvtColor(img, cv.COLOR_BGR2RGB)
        plt.imshow(img)
    plt.show()
def histogram(image):
    (row, col) = image.shape
    hist = [0]*256
    for i in range(row):
        for j in range(col):
            hist[image[i,j]] +=1
    return hist
def log(img,c=1,a=1):
    output = c * np.log2(1.0 + img)
    output = np.uint8(output + a)
    return output
img = cv.imread('iris.jpg')
show(img)
img_o = img
img_o[:,:,0]=log(img_o[:,:,0],c=25,a=20)
img_o[:,:,1]=log(img_o[:,:,1],c=25,a=20)
img_o[:,:,2]=log(img_o[:,:,2],c=25,a=20)
show(img_o)
img_hist_o = histogram(img_o[:,:,2])
plt.bar(range(256),img_hist_o)

运行结果：

a=10，c=10时的图像及三个通道的灰度直方图：