你们的电子宠物之勇闯嵌入式（C语言：第3天）

C语言：第三天

运算符

算数运算符

基本的算术运算符

+、-：正负值运算符（单目运算符）。

==+、-、*、/、%==加减乘除取余运算符（双目运算符）

表达式和运算符的优先级与结合性

算术表达式:是指用算术运算符和括号将运算对象连接起来，符合C语言语法规则的式子。例如:

a*b/c-1.5+'a'

• 表达式中各种运算符的运算顺序，必要时应添加括号，例如:

(a+b)/(c+d)!=a+b/c+d

• 优先级与结核性:在表达式求解的时候，先按运算符的优先级级别高低次序执行。若一个运算对象两侧的运算符的优先级相同，则按规定的结合方向处理。

各种运算的结合方向：

1. 算术运算的结合方向:自左向右即运算对象先与左边的运算符结合.

2. 有些运算符的结合方向:“自右向左"，即运算对象先与右边的运算符结合，例如:

i++

3. 若一个运算符两侧的数据类型不同，会自动转换成同类型后进行计算。

自增++、自减–运算符

作用：使变量值增1或者减1

结合方向：“ 自右向左 “

++i,–i

表示在使用该运算符对象之前，先让自身增1或减1，然后再使用它，也就是使用1或者减1的值。先计算，后赋值

例如:语句x=++n;相当于以下两个语句的运算结果:n=n+1;x=n;

int n=1;//n=1;
int x=++n;//x:2 等价于：n=n+1;x=n;

i++,i–

表后在使用该运算符对象之后，才让自身增1或者减1，也就是先使用，再让自身增1或者减1。先赋值，后计算

例如:语句x=n++;相当于以下两个语句的运算结果:x=n;n=n+1

int n=1;//n:1
int x=n++;//x:1,n:2等价于：x=n;n=n+1

总结:不管是++i还是i++，i自身都增1,同理不管是–i还是i–，i自身都减1。它们的不同之处在于赋值的先后顺序。

注意：

①增1与减1运算符只适用于整型变量或字符型变量，而不能用于其他类型的变量。

②)增1与减1运算符不能用于常量或表达式，例如:–5，(i+j)++ 等都是非法的。

练习

赋值运算符

“=”称之为赋值运算符，其作用是将一个数据赋值给一个变量。如:a=5。

• 实型→整型变量:舍弃小数部分。比如:int a=5.5;a应该是5
• 整型→实型变量:数值不变，以浮点形式存储。
• 字符型→整型变量:放在整型低8位。保持原值不变原则。比如:int a=‘A’

赋值表达式

主要实现赋值运算的表达式
语法:

变量=表达式

案例：

a=5;
y=2*x+3;
a=a+1;

作用:将右边表达式的值赋值给左边的变量。赋值表达式的值取自左边变量的值.

复合赋值运算符

+= -= *= %= .

左右两侧操作完毕后，赋值给左侧的变量，例如

a +=3;//等价于a=a+3
int c=2；
a /= c；//等价于a=a/c

注意：

1. 在运算时，不能将单括号(=)双括号(==)
2. 赋值运算符的优先级属于最低(除了逗号运算符以外)一般最后运算.

关系运算符

< > <= >= == !=

• 所有的关系运算符都是二元运算符，左侧和右侧可以是变量，也可以是常量，还可以是表达式;举例:a>b、5>6、a+b>c
• 关系运算符运算的结果是布尔类型，要么为真(非0，true)，要么为假(0，false)

说明：

1. 标准C中没有布尔类型的，非0代表真，0代表假。
   • while(0)循环一次都不执行
   • while(1)死循环，无限循环
2. 真在输出的结果为1，假在输出的结果为0
   • printf(“%d\n”,3<2); 结果为0
   • printf(“%d\n”,3>2);结果为1

说明：用作条件判断的时候，非0代表真，但是系统输出真的结果是1。

注意：

1. 算术运算符的优先级高于关系运算符。例如：2+3>1+1

2. 关系运算符是二元运算符，不要连用 例如：5>a>1(恒等于0) 3<b<10(恒等于1)可以编译和运行。前面案例正确的写法：a<5&&a>1,b>3&&b<10

3. 不能将*写成=*，：关系运算符，=：赋值运算符

4. 一般浮点型进行比较，建议将两个数相减，结果和0进行比较，如果等于0，表示这两个浮点数相等。

   案例1:

   float a=22.2

   float b=22.2

   a==b 结果为真；a！=b 结果为假 哪怕正确，也不要这样做

   案例2：

   float x=2.0;

   float y=11.1;//近似存储：11.099995

   float z=x*y //实际是：22.199999，我们以为：22.2

   z==22.2 结果为假

   两个浮点数的比较：两个浮点数相减跟0比

   a-b==0 结果是真，说明a等于b；如果是假，a不等于b

逻辑运算符

运算的结果要么是真(1)，要么是假(0)

！：非(逻辑非)单目运算符，并且只能放在操作数的左侧;非真即为假，非假即为真。(取反)

• 对一个数或者表达式取非奇数次，结果与原值相反，!(a%2!=0)取偶数次
• 对一个数或者表达式取非偶数次，结果与原值相反，!(a%2==0)取奇数次

&&：与(逻辑与)双目运算符，当左右两侧的数据都为真时，最终的结果才为真(有假则为假)

• 当逻辑与运算时，左侧为假右侧结果不会影响最终的结果，右侧压根就不会执行，最终结果为假，这种现象称为短路效果（短路与）。

||：或（逻辑或）双目运算符，当左右两侧的数据都为假时，最终结果才为假（有真则为真）

当逻辑或运算时，左侧为真，右侧结果不会影响最终的结果，右侧压根不会执行，最终结果为真，这种现象称为短路效果（短路或）。

惰性运算

所谓的惰性运算，就是减少运算次数。

• 短路与: && 两边的操作数，只要左边不成立0，直接返回假，不再校验右边。
• 短路或:|两边的操作数，只要左边成立1，直接返回真，不再校验右边。

逗号表达式

语法：

表达式1，表达式2，.....表达式n

求解过程:按从左到右的顺序分别计算个表达式值，其中最后一个表达式n的值就是整个逗号表达式的值。

位运算

说明：按位（bit）来进行运算操作的运算符。

语法： ~ & | << >>

~:按位取反

说明：单目运算符，数据的每一个bit位取反，也就是二进制数位上的0变11变0。

unsigned char ret = ~0x05;//0000 0101 -->1111 1010
printf("%d\n",~5);//-6  %d:有符号十进制int，%u：无符号十进制int

&:按位与

运算规则：对与左右操作数，只有相应的二进制位数据都为1时，结果数据对应数据为1，简单来说:

你是1，我是1，结果就是1

5 & 6 = 4; // 0000 0101 & 0000 0110 = 0000 0100

作用：

1. 获取某二进制位的数据
2. 将指定二进制数据清零
3. 保留指定位

| ：按位或

运算规则:对于左右操作数据，只要相应二进制位数据有一个为1，结果数据对应位数据为1，简单来说:

你是1 或 我是1 结果就是1

5 | 6 = 7 //0000 0101 | 0000 0111

作用：

1.置位某二进制数据

^:按位异或

运算规则：对与左右操作数据，只要相应二进制位数据相同，结果数据对应位数据为0，不同为1,简单来说

你我相同，结果为0;你我不同，结果为1

5 ^ 6 = 3 //0000 0101 | 0000 0111

作用：

1. 翻转
2. 值交换

面试题：

<<:左移，按位往左移

运算规则：原操作数所有的二进制位数向左移动指定位;

无符号左移

• 语法：操作数<<移动位数

unsigned int a=3<<3;//计算规则：3*2^3
unsigned int b=5<<4;//5*2^4
printf("%d",a);//24

有符号左移：

• 语法：操作数<<移动位数

int a=-3<<3;//-3*2^3
printf("%d\n",a);//-24

注意：

• 如果移出的高位都是0，可以这样理解：a<<n,可以看作：$$a\ast 2^n$$
• 如果移出的高位都是1，我们是不能使用上面的计算公式的。

>>：右移，按位往右偏移

运算规则:原操作数所有的二进制位数据向右移动指定位，移出的数据舍弃。

如果操作数是无符号数:左边用0补齐

如果操作数是有符号数:左边用什么去补全，取决于计算机系统

• 逻辑右移：用0补全
• 算术右移：用1补全

大部分情况下，系统是遵循“算术右移”的

无符号右移：

• 语法：操作数>>移动位数

unsigned char a=3>>3;
printf("%d\n",a);//0

有符号右移:

• 语法：操作数>>移动位数

char 3= -3>>3;
printf("%d\n",a);//-1

流程控制

算法

著名计算机科学家沃思提出了一个公式:

数据结构+算法=程序

数据结构：对数据的描述

算法：对操作步骤进行的描述

算法定义

广义的说，未解决一个问题而采取的方法和有限的步骤，就称为“算法

例如：

将大象放入冰箱的算法就可以如下描述：
打开冰箱门-把大象装进去-关闭冰箱门

算法特征

• 有穷性:包含有限的操作步骤，不能无限制的执行下去
• 可行性:算法中的每一条指令必须是切实可执行的。(a<0 &&a>=100)
• 确定性:算法中的每一条指令必须有确切的含义，不能产生歧义。

程序的三种基本结构

顺序结构

特点：各操作是按先后顺序执行的，是最简单的一种结构，这个结构是默认的。

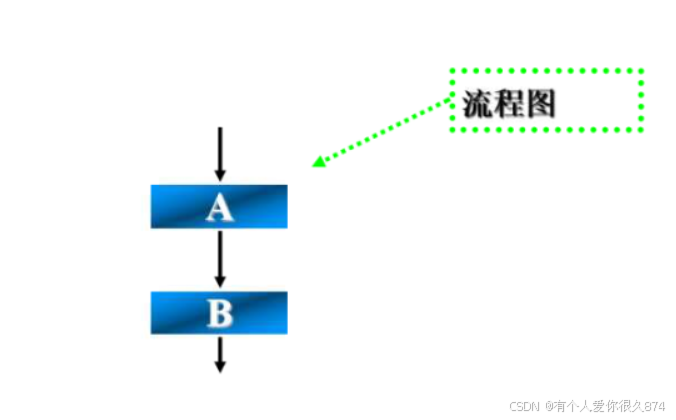
其中A和B两个框是顺序执行的。也就是在A框所指定的操作后，必然接着执行B框所指定的操作。

分支结构

分支结构又被称作“条件结构”或者“选择结构”。

特点:根据是否满足给定条件而从两组或者多组操作中选择一种进行执行。

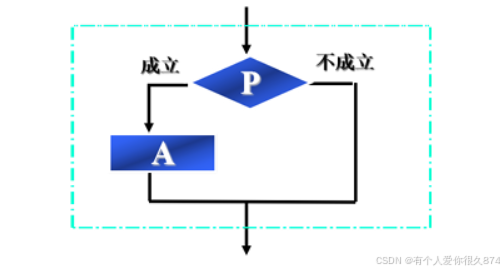
• ⽆论P条件是否成⽴，只能执⾏A操作或者B操作中的⼀个。
• ⽆论执⾏完哪⼀个分⽀后，就结束了

分支结构又被分为：单分支、双分支、多分支

循环结构

又被称之为“重复结构”。即在一定条件下，反复执行某一部分的操作，有两种类型:

• 当型循环

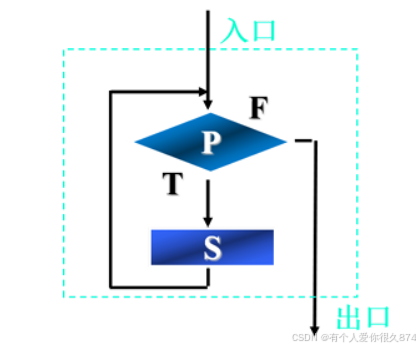
• 执行过程：当给定条件P成⽴时，执⾏S操作，然后再判断P条件是否成⽴，如果仍成⽴，再执⾏S操作，然后再判 断…，如此反复，直到某⼀次P条件不成⽴为⽌，此时不再执⾏S，结束循环。

• 特点：

  • 先判断，后执⾏，S有可能⼀次也不执⾏。(while，for）

• 直到型循环

  • 执⾏过程：
  • 执⾏S操作，然后判断条件P是否成⽴，如果成⽴，再执⾏S操作，然后再判断，……，如此反复，直到某 ⼀次P条件不成⽴不再执⾏S，结束循环。

• 特点：
  ⼀个。

• ⽆论执⾏完哪⼀个分⽀后，就结束了

分支结构又被分为：单分支、双分支、多分支

循环结构

又被称之为“重复结构”。即在一定条件下，反复执行某一部分的操作，有两种类型:

• 当型循环

[外链图片转存中…(img-u7tVCBFn-1732700632398)]

• 执行过程：当给定条件P成⽴时，执⾏S操作，然后再判断P条件是否成⽴，如果仍成⽴，再执⾏S操作，然后再判 断…，如此反复，直到某⼀次P条件不成⽴为⽌，此时不再执⾏S，结束循环。

• 特点：

  • 先判断，后执⾏，S有可能⼀次也不执⾏。(while，for）

• 直到型循环

  • 执⾏过程：
  • 执⾏S操作，然后判断条件P是否成⽴，如果成⽴，再执⾏S操作，然后再判断，……，如此反复，直到某 ⼀次P条件不成⽴不再执⾏S，结束循环。

• 特点：

  • 先执⾏，后判断，S最少要执⾏⼀次。(do…while)