网站流量异常检测

最新推荐文章于 2025-05-04 20:00:00 发布

原创最新推荐文章于 2025-05-04 20:00:00 发布

· 1.4k 阅读

20 ·

版权

文章标签：

#机器学习 #java #spring boot

Java机器学习专栏收录该内容

20 篇文章

订阅专栏

第二个例子中，我们将对前一个例子的反面建模。我们不会讨论典型的少欺诈案例是什么，而要讨论系统正常的预期行为。如果有违背模型预期的事情发生，这个事情就会被识别为异常。

创建工程

接着前面的项目：

数据集

我们将使用一个Yahoo Labs公开的数据集，这有助于我们研究如何从时序数据中检测异常。对于Yahoo而言，主要使用案例是检测Yahoo服务器上的非正常流量。

数据集由流向Yahoo服务的真实流量组成，里面同时含有一些合成数据。这个数据集总共包含367个时间序列，每个时序包含741~1680个观察结果，它们是按固定时间间隔记录得到的。每个序列都有自己的记录文件，每一行对应一个观察结果。每个序列都带有一个列指示器——“异常”（anomaly），观察表明这个序列是异常时，该列值为1，否则为0。实际数据中的异常由人为判断决定，而合成数据中的异常由算法自动生成。

接下来，我们将学习如何将时序数据转换为属性，以便应用机器学习算法。

时序数据中的异常检测

在原始流式时序数据中检测异常时，需要对数据做一些转换。最明显的做法是选择一个时间窗口，用固定长度采集时间序列。接下来，我们比较新时间序列与之前采集的序列，以检测是否有异常发生。
可以选用的比较技术多种多样：

 预测最有可能的跟随值（following value）以及置信区间（比如霍尔特-温特指数平滑）。若新值超出预测的置信区间，即被判定为异常。

 互相关（Cross correlation）技术比较新样本与正例样本库，查找准确匹配。若未发现匹配，则把新样本标记为异常。

 动态时间规整与互相关类似，但它允许比较中有信号失真。

 信号离散化到频带，每个频带对应于一个字母，比如 A=[min, mean/3] 、 B=[mean/3, mean*2/3]、C=[mean*2/3, max]，将信号转换为字母序列，比如aAABAACAABBA….这个方法可以有效减少存储，并且允许我们使用文本挖掘算法。文本挖掘相关内容将在第10 章讲解。

 基于分布的方法评估一个特定时间窗口中值的分布。观察一个新样本时，可以将其分布与之前观察的进行比较，查看是否匹配。

上述列表并不全面，这些不同方法都将重点放在检测某些异常上（比如值异常、频率异常、分布异常）。接下来将重点讲解基于分布的方法。

基于直方图的异常检测

基于直方图的异常检测中，通过某个选定的时间窗口对信号做切分

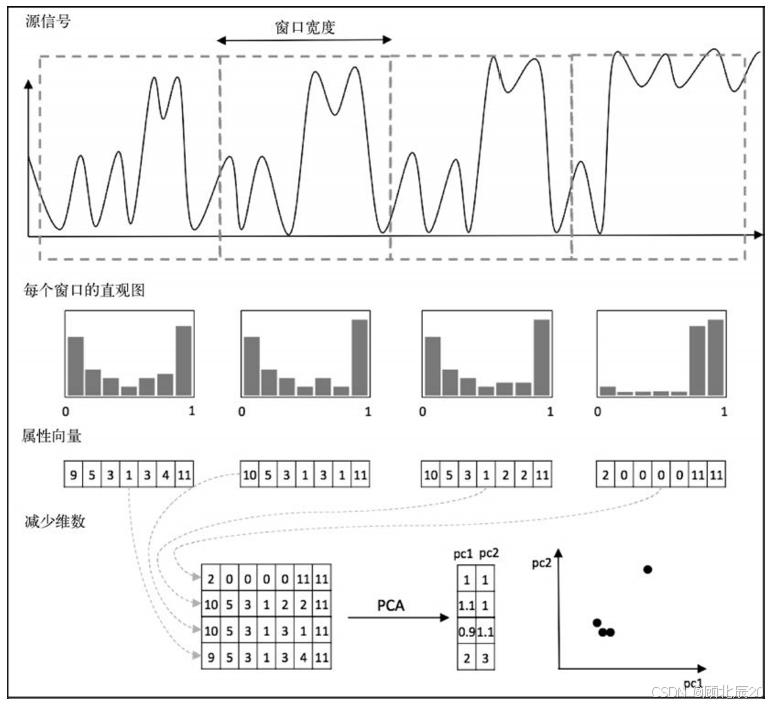
针对每个窗口计算直方图，也就是说，针对选中的桶数，计算每个桶中落入多少个值。直方图反映了所选时间窗口中值的分布情况（下图中间部分）。

然后，可以直接把直方图表示成实例，每个bin对应一个属性。而且，通过应用维度缩减技术（比如主成分分析，PCA），可以减少属性数目，这样就可以使用散点图绘制降维后的直方图，其中每个点代表一个直方图（下图右下）。

我们的示例中，主要的想法是先对网站流量观察几天，然后创建直方图，比如以4小时为窗口创建一个正常行为库。若新时间窗口直方图与正常行为库不匹配，就将其标记为异常。

比较一个新的直方图与一组已有的直方图时，我们会使用基于密度的k最近邻算法——局部异常因子算法（LOF，Breunig等，2000）。这个算法能够处理拥有不同密度的群组（clusters），如图所示。比如，相比于左下方小而密集的群组，右上方群组既大又广。

加载数据

第一步中，我们需要把数据从文本文件加载到一个Java对象。这些文本文件存储在一个文件夹，每个文件中，每一行就是一个带有值的时间序列。我们将其加载到一个Double型列表：

        /*
         * 加载数据
         */
        String path = ClassUtils.getDefaultClassLoader().getResource("data/test07/ydata/A1Benchmark").getPath() + "/real_";
        List<List<Double>> rawData = new ArrayList<List<Double>>();

对直方图做正态化处理的过程中，要用到min与max值。因此数据传递时，需要先得到它们。

        double max = Double.MIN_VALUE;
        double min = Double.MAX_VALUE;
        // 读取67个CSV文件
        for (int i = 1; i <= 67; i++) {
            List<Double> sample = new ArrayList<Double>();
            BufferedReader reader = new BufferedReader(new FileReader(path + i + ".csv"));
            boolean isValid = false;
            // 跳过第一行（标题行）
            reader.readLine();
            while (reader.ready()) {
                String line = reader.readLine();
                String[] str = line.split(",");
                double value = Double.parseDouble(str[1]);
                // 添加值到sample列表
                sample.add(value);
                // 更新最大值和最小值
                if (value > max) max = value;
                if (value < min) min = value;
                // 检查是否是有效的样本
                if ("1".equals(str[2])) {
                    isValid = true;
                }
            }
            // 打印是否是有效样本
            System.out.println(isValid);
            // 关闭reader
            reader.close();
            // 将样本添加到rawData列表
            rawData.add(sample);
        }
        // 打印加载的样本数量、最大值和最小值
        System.out.println("size:" + rawData.size() + "\tmax: " + max + "\tmin: " + min);

至此，数据加载完毕，接下来开始创建直方图。

创建直方图

我们将按照WIN_SIZE宽度为选定的时间窗口创建直方图。这个直方图用于存储HIST_BINS 值桶（value buckets）。这些包含double列表的直方图会被存储到一个数组列表。

        /*
         * 创建直方图
         */
        // 创建delta_t直方图
        int WIN_SIZE = 500; // 窗口大小
        int HIST_BINS = 20; // 直方图的 bins 数量
        int current = 0;
        List<double[]> dataHist = new ArrayList<double[]>();
        // 遍历每个样本
        for (List<Double> sample : rawData) {
            double[] hist = new double[HIST_BINS];
            for (Double value : sample) {
                int bin = toBin(normalize(value, min, max), HIST_BINS);
                hist[bin]++;
                current++;
                // 如果当前窗口达到窗口大小，重置计数器并添加直方图
                if (current == WIN_SIZE) {
                    current = 0;
                    dataHist.add(hist);
                    hist = new double[HIST_BINS];
                }
            }
            // 添加最后一个窗口的直方图
            dataHist.add(hist);
        }

直方图已经做好，接下来要把它们转换为Weka中的Instance对象。每个直方图值对应于一个Weka属性，代码如下：

        /*
         * 创建数据库
         */
        ArrayList<Attribute> attributes = new ArrayList<Attribute>();
        for (int i = 0; i < HIST_BINS; i++)
            attributes.add(new Attribute("HIST-" + i));
        // 创建数据集
        Instances data = new Instances("data", attributes, dataHist.size());
        for (double[] hist : dataHist) {
            data.add(new DenseInstance(1.0, hist));
        }
        // 打印数据集大小
        System.out.println("Dataset created: " + data.size());

至此，我们已经加载好数据集，接下来应用异常检测算法。

基于密度的k最近邻算法

为了演示LOF算法（即局部异常因子算法）如何计算分数，先使用testCV(int, int)函数把数据集划分为训练集与测试集。其中，第一个参数用于指定折数，第二个参数指定要返回哪个折。

        /*
         * 构建模型
         */
        // 将数据分为训练集和测试集
        Instances trainData = data.testCV(2, 0);
        Instances testData = data.testCV(2, 1);
        System.out.println("Train: " + trainData.size() + "\nTest:" + testData.size());

LOF算法有两个实现接口：一个用作无监督过滤器，计算LOF值（已知的未知）；另一个用作监督k-nn分类器（已知的已知）。我们的示例要计算异常分数因子（outlier-ness factor），所以将使用无监督过滤器接口。

使用常规过滤器的初始化方式对这个过滤器进行初始化。可以指定邻居的k数（比如k=3）以及-min与-max参数。LOF允许我们指定两个不同的k参数，在内部一个用作上界，另一个用作下界，以便查找最小/最大数lof值：

        // 加载训练数据到 k-NN 算法
        LOF lof = new LOF();
        lof.setInputFormat(trainData);
        lof.setOptions(new String[]{"-min", "3", "-max", "3"});

接下来，将训练实例加载到过滤器，用作正例库。加载完成后，调用batchFinished()方法对内部计算做初始化：

        for (Instance inst : trainData) {
            lof.input(inst);
        }
        lof.batchFinished();

最后，将过滤器应用于测试数据。过滤器将处理实例，并在最后添加一个包含LOF评分的属性。我们可以在控制台简单输出分数。

        // 打印 LOF 模型加载完成
        System.out.println("LOF loaded");
        // 对测试数据进行过滤
        Instances testDataLofScore = Filter.useFilter(testData, lof);
        for (Instance inst : testDataLofScore) {
            // 打印 LOF 得分
            System.out.println(inst.value(inst.numAttributes() - 1));
        }

前面几个测试实例的LOF分数如下：

1.306740014927325 
1.318239332210458 
1.0294812291949587 
1.1715039094530768

为了理解LOF值，需要先了解LOF算法。LOF算法比较一个实例的密度与其最近邻的密度，两个分数相除就是LOF分数。若LOF分数接近1，则表示密度近似相等。LOF值越大，表示实例密度越低于它邻居的密度。这些情况下，实例会被标记为异常。

完整代码

public class Anomaly {
    public static void main(String[] args) throws Exception {
        /*
         * 加载数据
         */
        String path = ClassUtils.getDefaultClassLoader().getResource("data/test07/ydata/A1Benchmark").getPath() + "/real_";
        List<List<Double>> rawData = new ArrayList<List<Double>>();
        double max = Double.MIN_VALUE;
        double min = Double.MAX_VALUE;
        // 读取67个CSV文件
        for (int i = 1; i <= 67; i++) {
            List<Double> sample = new ArrayList<Double>();
            BufferedReader reader = new BufferedReader(new FileReader(path + i + ".csv"));
            boolean isValid = false;
            // 跳过第一行（标题行）
            reader.readLine();
            while (reader.ready()) {
                String line = reader.readLine();
                String[] str = line.split(",");
                double value = Double.parseDouble(str[1]);
                // 添加值到sample列表
                sample.add(value);
                // 更新最大值和最小值
                if (value > max) max = value;
                if (value < min) min = value;
                // 检查是否是有效的样本
                if ("1".equals(str[2])) {
                    isValid = true;
                }
            }
            // 打印是否是有效样本
            System.out.println(isValid);
            // 关闭reader
            reader.close();
            // 将样本添加到rawData列表
            rawData.add(sample);
        }
        // 打印加载的样本数量、最大值和最小值
        System.out.println("size:" + rawData.size() + "\tmax: " + max + "\tmin: " + min);
        /*
         * 创建直方图
         */
        // 创建delta_t直方图
        int WIN_SIZE = 500; // 窗口大小
        int HIST_BINS = 20; // 直方图的 bins 数量
        int current = 0;
        List<double[]> dataHist = new ArrayList<double[]>();
        // 遍历每个样本
        for (List<Double> sample : rawData) {
            double[] hist = new double[HIST_BINS];
            for (Double value : sample) {
                int bin = toBin(normalize(value, min, max), HIST_BINS);
                hist[bin]++;
                current++;
                // 如果当前窗口达到窗口大小，重置计数器并添加直方图
                if (current == WIN_SIZE) {
                    current = 0;
                    dataHist.add(hist);
                    hist = new double[HIST_BINS];
                }
            }
            // 添加最后一个窗口的直方图
            dataHist.add(hist);
        }
        // 归一化直方图
        for (double[] hist : dataHist) {
            double sum = 0;
            for (double d : hist) {
                sum += d;
            }
            for (int i = 0; i < hist.length; i++) {
                hist[i] /= sum;
            }
        }
        // 打印总数直方图
        System.out.println("Total histograms:" + dataHist.size());
        /*
         * 创建数据库
         */
        ArrayList<Attribute> attributes = new ArrayList<Attribute>();
        for (int i = 0; i < HIST_BINS; i++)
            attributes.add(new Attribute("HIST-" + i));
        // 创建数据集
        Instances data = new Instances("data", attributes, dataHist.size());
        for (double[] hist : dataHist) {
            data.add(new DenseInstance(1.0, hist));
        }
        // 打印数据集大小
        System.out.println("Dataset created: " + data.size());
        /*
         * 构建模型
         */
        // 将数据分为训练集和测试集
        Instances trainData = data.testCV(2, 0);
        Instances testData = data.testCV(2, 1);
        System.out.println("Train: " + trainData.size() + "\nTest:" + testData.size());
        // 加载训练数据到 k-NN 算法
        LOF lof = new LOF();
        lof.setInputFormat(trainData);
        lof.setOptions(new String[]{"-min", "3", "-max", "3"});
        for (Instance inst : trainData) {
            lof.input(inst);
        }
        lof.batchFinished();
        // 打印 LOF 模型加载完成
        System.out.println("LOF loaded");
        // 对测试数据进行过滤
        Instances testDataLofScore = Filter.useFilter(testData, lof);
        for (Instance inst : testDataLofScore) {
            // 打印 LOF 得分
            System.out.println(inst.value(inst.numAttributes() - 1));
        }
    }

    /**
     * 将值归一化到 [0, 1] 区间
     *
     * @param value 值
     * @param min   最小值
     * @param max   最大值
     * @return 归一化后的值
     */
    static double normalize(double value, double min, double max) {
        return (value - min) / (max - min);
    }

    /**
     * 返回一个 bin，范围在 [0, bins)。假设值已归一化到 [0, 1] 区间
     *
     * @param normalizedValue 归一化后的值
     * @param bins            bins 数量
     * @return bin 编号
     */
    static int toBin(double normalizedValue, int bins) {
        if (normalizedValue == 1.0) return bins - 1;
        return (int) (normalizedValue * bins);
    }
}