代码随想录算法Day1 （数组理论基础，704二分查找，27移除元素）

一、数组理论基础

文档讲解

https://programmercarl.com/%E6%95%B0%E7%BB%84%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html

数组是存放在连续内存空间上的相同类型数据的集合。

需要两点注意的是

• 数组下标都是从0开始的。
• 数组内存空间的地址是连续的

正是因为数组的在内存空间的地址是连续的，所以我们在删除或者增添元素的时候，就难免要移动其他元素的地址。

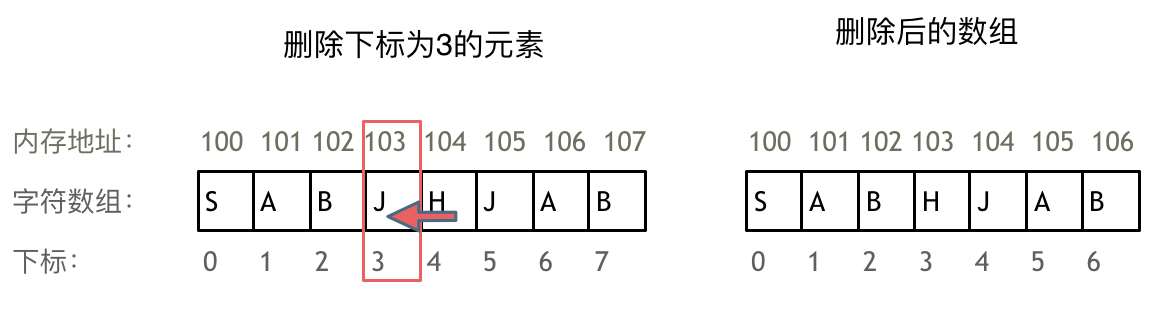
例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

 二、二分查找

文档讲解代码随想录 (programmercarl.com)

题目链接704. 二分查找 - 力扣（LeetCode）

视频讲解

手把手带你撕出正确的二分法 | 二分查找法 | 二分搜索法 | LeetCode：704. 二分查找_哔哩哔哩_bilibili

二分查找需要的条件

• 用于查找的内容逻辑上来说是需要有序的
• 查找的数量只能是一个，而不是多个

        在二分查找中，目标元素的查找区间的定义十分重要，不同的区间的定义写法不一样，因为查找的区间是不断迭代的，所以确定查找的范围十分重要，主要就是左右区间的开和闭的问题，开闭不一样，对应的迭代方式也不一样，有以下两种方式：

        左闭右闭[left, right]

        左闭右开[left, right)

题目：

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例 1:

输入:nums= [-1,0,3,5,9,12],target= 9
输出: 4
解释: 9 出现在nums中并且下标为 4

示例 2:

输入:nums= [-1,0,3,5,9,12],target= 2
输出: -1
解释: 2 不存在nums中因此返回 -1

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

思路一：循环遍历

遍历整个数组，若与目标值数值相同，则返回该数下标，若未找到目标值，则返回-1.

//循环遍历
class Solution {
    public int search(int[] nums, int target) {
        for(int i = 0;i<nums.length;i++){
            if(nums[i]==target){
                return i;
            }
        }
        return -1;
    }
}

结果：通过，但用时较长。

思路二：二分查找，左闭右闭

左闭右闭区间 [left,right]

因为定义target在[left, right]区间，所以有如下两点：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

自己编写：

//二分查找
class Solution {
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length-1;
        while(left<=right){
            int mid = (left + right)/2;
            if(target==nums[mid]){
                return mid;
            }else if(target>nums[mid]){
                left=mid+1;
            }else{
                right=mid-1;
            }

        }
        return -1;
    }
}

补充：

class Solution {
    public int search(int[] nums, int target) {
        // 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
        if (target < nums[0] || target > nums[nums.length - 1]) {
            return -1;
        }
        int left = 0, right = nums.length - 1;// 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int mid = left + ((right - left) >> 1); // 防止溢出 等同于(left + right)/2
            if (nums[mid] == target)
                return mid;  // 数组中找到目标值，直接返回下标
            else if (nums[mid] < target)
                left = mid + 1;  // target 在右区间，所以[middle + 1, right]
            else if (nums[mid] > target)
                right = mid - 1;  // target 在左区间，所以[left, middle - 1]
        }
        return -1;  // 未找到目标值
    }
}

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

思路三：二分查找，左闭右开

• while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
• if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

class Solution {
    public int search(int[] nums, int target) {
        int left=0,right=nums.length;
        while(left<right){
            int mid = (left+right)/2;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]<target){
                left=mid+1;
            }else if(nums[mid]>target){
                right=mid;
            }
        }
        return -1;
    }
}

• 时间复杂度：O(log n)
• 空间复杂度：O(1)

三、移除元素

思路一：暴力解法

暴力的解法就是两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。

class Solution {
    public int removeElement(int[] nums, int val) {
        int len = nums.length;
        for(int i=0;i<len;i++){
            if(nums[i]==val){
                for(int j=i+1;j<len;j++){
                    nums[j-1]=nums[j];
                }
                i--;
                len--;
            }
        }
        return len;
    }
}

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)

思路二：双指针法

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针

• 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
• 慢指针：指向更新 新数组下标的位置

很多同学这道题目做的很懵，就是不理解 快慢指针究竟都是什么含义，所以一定要明确含义，后面的思路就更容易理解了。

删除过程如下:

class Solution {
    public int removeElement(int[] nums, int val) {
        int slow = 0;
        for(int fast=0;fast<nums.length;fast++){
            if(nums[fast]!=val){
                nums[slow]=nums[fast];
                slow++;
            }

        }
        return slow;
    }
}

总结

第一天的学习到此结束，熟悉了学习流程，博客的书写，不足之处是太懒惰......