139、★LeetCode-柱状图中最大的矩形

题目：

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

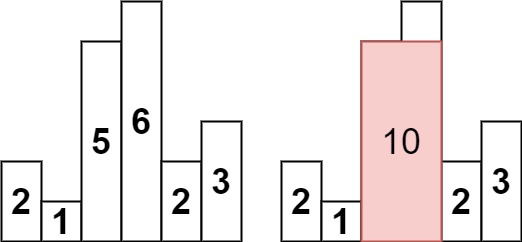
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/largest-rectangle-in-histogram

思路：

单调栈：在一维数组中，遇到找两侧最值的问题，经常就是单调栈的问题；

需要考虑栈中存储数值还是下标！

接雨水和本题虽然没有直接指出找最值，但是通过分析，还是找最值问题，可以使用单调栈解决问题：

接雨水：按列计算，往两侧找最大值；

本题：往两侧找第一个小于当前值的值！按照栈底到栈顶递增：出现小于栈顶元素的情况时，就是右侧小于当前值的第一个值出现；栈中一直保持递增(相等的问题不好处理，但是更靠近栈底的数字就包含了所有情况)，前一个元素就是左侧第一个！

1）暴力：for中套while，往两侧找，时间复杂度大

2）单调栈：本题中会出现：最后栈中保持递增，有许多位置无法处理的情况！对数组扩容，两则加上不改变体积的数值0即可！

注意坐标的考虑，栈中紧挨着，不代表数组中紧挨着！

3）动态规划：类似接雨水；时间复杂度还要更好一点

记录每个位置上，左边和右边第一个小于其值的下标！

代码：

1）暴力解法：时间复杂度O(N^2)，无法通过

class Solution {
    public int largestRectangleArea(int[] heights) {
        
        //本题是找矩形：因此只有一个矩形，且需要一个高；每个位置都能充当一个高！只招一种情况
        //接雨水：将每个列都当作一次底座！将所有列的雨水情况找到，相加就是结果！
        int l = heights.length;
        int res = 0;
        //分别往最左和最右找最后一个大于等于的下标!
        //接雨水，是往左和往右，找第一个大于！
        for(int i = 0;i < l;i++){
            int left = i;//从当前位置开始，往左找
            while(left >= 0 &&  heights[left] >= heights[i]){
                left--;
            }
            int right = i;//从当前位置开始，往右找
            while(right < l && heights[right] >= heights[i]){//找最后一个大于等于的下标
                right++;
            }
            
            int sum = (right - left - 1) * heights[i];
            res = Math.max(res,sum);
        }
        return res;
    }
}

2）单调栈：

class Solution {
    public int largestRectangleArea(int[] heights) {
    
        //单调栈：之前说明，是往左往右找第一个小于其值的位置；
        //只用使用单调栈记录顺序即可，就能够o1找到
        //这道题的单调栈刚好和接雨水相反！
        int res = 0;

        //正常处理单调栈，会存在最后栈中保留了递增的元素，有一些情况无法处理
        //将数组两端扩容，存放两个不会改变体积的 0；
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }
        heights = newHeights;
        int l = heights.length;

        Deque<Integer> stack = new LinkedList<>();

        //整体的思想还是，找到每一列，以每一列为高，计算其构成的矩形
        for(int i = 0;i < l;i++){
            while(!stack.isEmpty() && heights[i] < heights[stack.peek()]){
                //此时需要处理栈中的情况了：从栈底到栈顶是递增的，因为后面要入栈的都是其右边，碰见小于的前面的就需要处理了
                int h = stack.pop();//表示高
                int num = heights[h] * (i - stack.peek() - 1);
                //当前要入栈的节点处，才是问题的关键；只有当他比栈内余下的元素都大时，才能入栈！
                //只要他比栈内的元素小，就需要按顺序处理栈内的元素！
                res = Math.max(res,num);
            }
            //相等时，入不入栈都可以，入栈就是多计算！
            stack.push(i);//每个位置都要处理
        }
       return res;
    }
}

3）动态规划

class Solution {
    public int largestRectangleArea(int[] heights) {
        //动态规划
        int length = heights.length;
        int[] minLeftIndex = new int [length];
        int[] maxRigthIndex = new int [length];
        // 记录左边第一个小于该柱子的下标
        //初始化都考虑到了宽度的计算！
        minLeftIndex[0] = -1 ;
        for (int i = 1; i < length; i++) {
            int t = i - 1;
            // 这里不是用if，而是不断向右寻找的过程
            while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
            minLeftIndex[i] = t;
        }
        // 记录每个柱子 右边第一个小于该柱子的下标
        maxRigthIndex[length - 1] = length;
        for (int i = length - 2; i >= 0; i--) {
            int t = i + 1;
            while(t < length && heights[t] >= heights[i]) t = maxRigthIndex[t];
            maxRigthIndex[i] = t;
        }
        // 求和
        int result = 0;
        for (int i = 0; i < length; i++) {
            int sum = heights[i] * (maxRigthIndex[i] - minLeftIndex[i] - 1);
            result = Math.max(sum, result);
        }
        return result;
    }
}