C++希尔排序

---

前言

今天来和大家一起学习希尔排序。

---

以下是本篇文章正文内容。

一、希尔排序的基础知识点

1.希尔排序的排序原理

1959年Shell发明而得名，第一个*突破O(n2)*的排序算法，其实希尔排序本质上是一种特殊的插入排序，它与插入排序不同在于它会优先比较距离较远的元素。希尔排序又名“缩小增量排序”。
我们一般使用希尔排序时，会定义一个距离变量k(这里假设是k)，相距k的元素之间比较大小并判断是否交换位置，k通常为数组的一半长，每次循环完k都缩小一半，最后k = 1。完成排序

2.希尔排序的所属类别

因为希尔排序是一种特殊的插入排序，所以希尔排序和插入排序一样，都属于比较类排序。

3.希尔排序的算法复杂度

希尔排序的时间复杂度是O（n的1.25次方zhi）~O(1.6n的1.25次方)

二、希尔排序的动态图

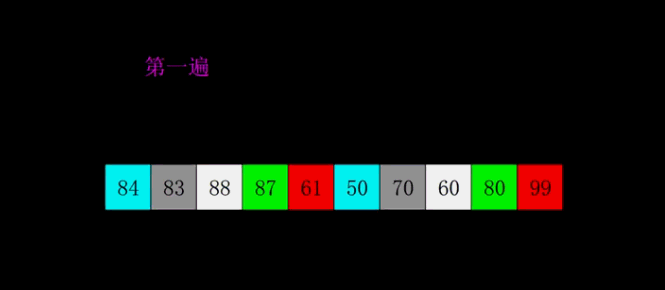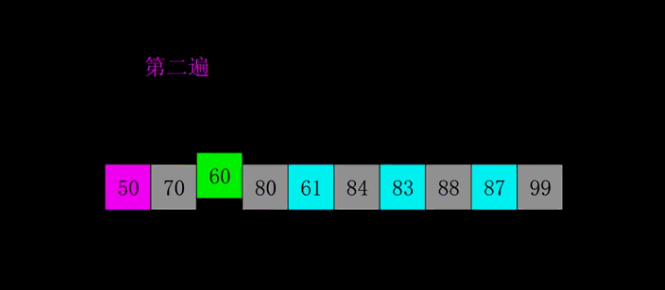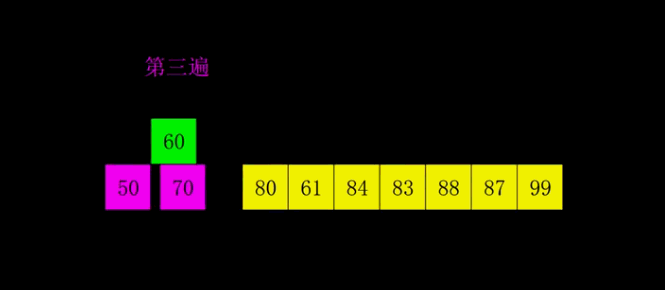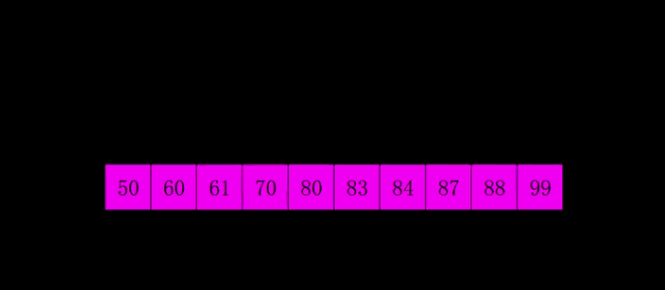
大家可以看到，距离第一遍为(10/2) = 5,再为2，再为1。所以希尔排序就是不断地减半比较距离，当距离为1的排序也排完之后，便完成了希尔排序。

三、希尔排序的代码与执行情况

代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
	int n, count, k, i, current;
	cin >> n;
	int a[999];    //取一个较大的数组 
	for(count = 1; count <= n; count++)
	    cin >> a[count];    //把每一个数字输入到数组内,共输入n个数
    //k为距离，一般第一次取序列长度的一半/每次循环k缩小一半 
	for(k = n/2; k>=1; k/=2)    
	{
	    for(count = 1; count <= n-k; count++)
		{
			i = count;    //用i来缓存一下count
			current = a[count];
			if(a[count] >= a[count+k])    //若位于前面的数较大 
			{
				a[count] = a[count+k];    //则两数位置互换
				a[count+k] = current;
			}
		}
	}  
	for(count = 1; count <= n; count++)
	cout << a[count] << " ";      //输出数组
	return 0;
}

2.执行情况

情况如下：

---

总结

以上就是今天要讲的内容，本文仅仅简单介绍了希尔排序的使用，但笔者不太清楚希尔排序的时间复杂度的证明方法，希望有明白证明方法的朋友可以和大家讲一讲。笔者不才，若有错误，愿大家提出，笔者定及时纠正。愿与大家同学习，共进步！