2021-09-10

2021 [牛客6H] Hopping Rabbit

线段树+扫描线

题面：



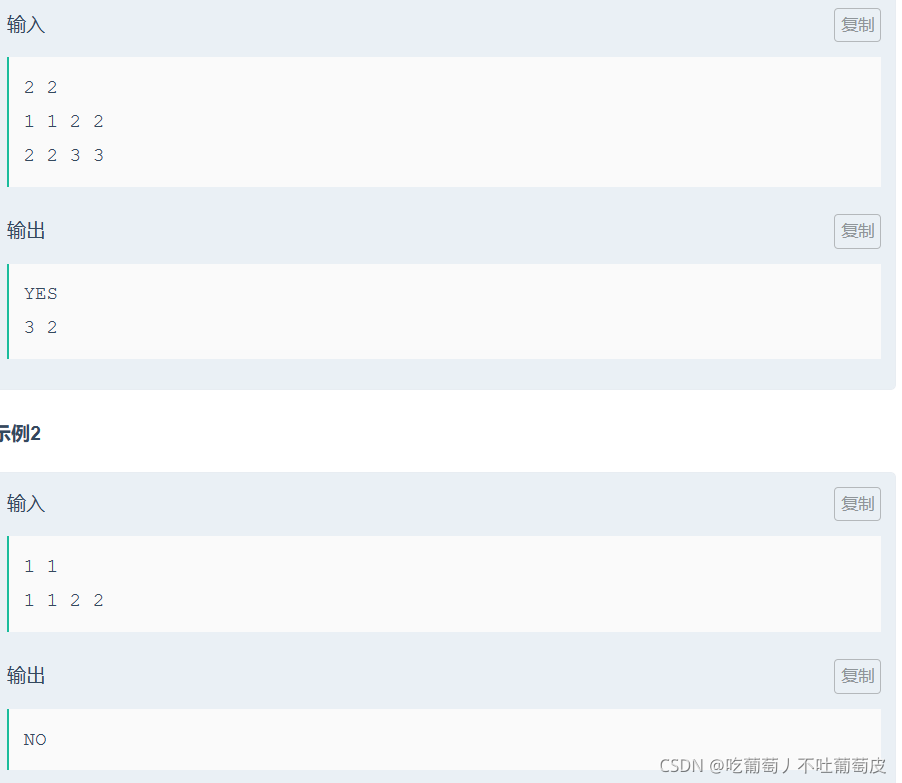
题目大意:
二维直角坐标系中，n个陷阱，每个陷阱是一个矩形，给你左下角和右上角两个点坐标(x1,y1),(x2,y2)。主人公是一只兔子，每次能且只能跳距离d，而且只有上下左右四个方向，兔子不能跳入陷阱，现在让你求一个点可以让兔子无论怎么跳都不会跳入陷阱（输出任意一个可行解即可）.

思路：
如果我们把整张图分成许多dd的小正方形,就会出现如图的情况

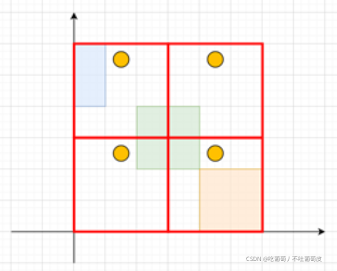
其中的黄色圆点就是我们想要找的点,我们可以看到如果我们将每个dd小块中被矩形占据的位置"移动"到左下角的小块中,就会出现如图的情况

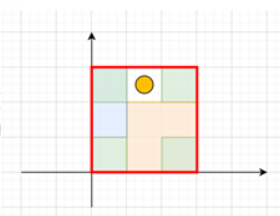
其实就是把每个dd的方格内的陷阱转移到同一个d*d的方格内，没有被覆盖的点就是可行解
用扫描线，扫到某一条没有完全被覆盖，那么一定有可行解。
具体操作
step1：陷阱转移（注意x1,x2,y1,y2大小的变化)，就是取模
step2：对于矩形：左下角（x1,y1),右上角(x2,y2),差分思想，我们在坐标为 x1处建立一棵线段树，区间[y1,y2]都+1，在x2+1处建立线段树，区间[y1,y2]都-1,(当然，同一个坐标只建一棵线段树，区间修改),节点维护cnt:这个区间被覆盖了多少次,len:这个区间被覆盖的长度
step3: 从0到d-1扫描，对于每个i，若它的tree[1].len<n，那么就没有覆盖完全，x轴坐标为i处一定有解，再去线段树中查找一下

注意：
输入的x2–,y2–;化点为格，现在求出的一个坐标为小格子的位置

AC代码

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<iostream>
#include<vector>
using namespace std;
const int maxn=100000+10;
int n,d;
struct point{
	int l,r,flag;
};
struct node{
	int len,cnt;
	//当前区间整个被覆盖多少次(对应图中的1，-1)
	//当前区间cnt>0的区间总长和
}tree[maxn*4];
vector<point> sm[maxn];
void mod(int &x) {//取模
	x %= d;
	while (x < 0)
		x += d;
}
void add(int x1,int x2,int y1,int y2){//扫描线 
	point tmp;
	tmp.l =y1;tmp.r =y2;tmp.flag =1;
	sm[x1].push_back(tmp); 
	tmp.flag =-1;
	sm[x2+1].push_back(tmp);  
}
void download(int id,int l,int r)
{
	if(tree[id].cnt )	tree[id].len =r-l+1;
	else if(l==r) tree[id].len =0;
	else tree[id].len =tree[id*2].len +tree[id*2+1].len ;
}
void update(int id,int l,int r,int L,int R,int val)
{
	if(l>=L&&r<=R)
	{
		tree[id].cnt +=val;
		download(id,l,r);//不用传递cnt，因为最后只是求tree[1].len 
		return ;
	}
	int mid=(l+r)/2;
	if(L<=mid) update(id*2,l,mid,L,R,val);
	if(R>mid)  update(id*2+1,mid+1,r,L,R,val);
	//tree[id].len =tree[id*2].len +tree[id*2+1].len ;
	download(id,l,r);
}

void query(int id,int l,int r)
{
	if(tree[id].len ==0)
	{
		printf("%d",l);
		return;
	}
	int mid=(l+r)/2;
	if(tree[id*2].len <mid-l+1) query(id*2,l,mid);
	else query(id*2+1,mid+1,r);
}

int main()
{
	scanf("%d%d",&n,&d);
	int x1,y1,x2,y2;
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		x2--;y2--;
		//比如说(1,1) (2,2) ,减了之后为(1,1),(1,1)，当走到（1，1）的时候代表在实际图中走到了方块内部 
		//注：例如（-13）%5=-3； 
		if(x2-x1+1>=d)	x1=0,x2=d-1;
		if(y2-y1+1>=d)  y1=0,y2=d-1;
		mod(x1), mod(x2), mod(y1), mod(y2);
		if(x1<=x2)
		{
			if(y1<=y2)	add(x1,x2,y1,y2); 
			else	add(x1,x2,0,y2),add(x1,x2,y1,d-1);
		} 
		else
		{
		 	if(y1<=y2) add(0,x2,y1,y2),add(x1,d-1,y1,y2);
		 	else add(0,x2,0,y2),add(x1,d-1,y1,d-1),add(0,x2,y1,d-1),add(x1,d-1,0,y2);
		}
		
	}
	for(int i=0;i<d;i++)
	{
		int s=sm[i].size() ;
		for(int j=0;j<s;j++)   update(1,0,d-1,sm[i][j].l,sm[i][j].r,sm[i][j].flag);
		if(tree[1].len <d)
		{
			printf("YES\n%d ",i);
			query(1,0,d-1);	
			return 0;
		}
	}
	printf("NO");
	return 0;
}