【Java】每日一题，礼物的最大价值

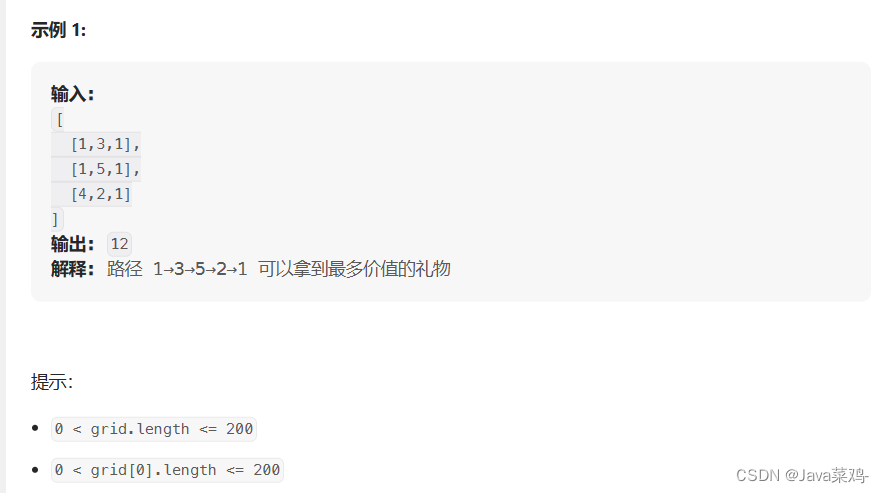
在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

 题目分析

  拿到最多价值的礼物即我们需要找出从矩阵左上角至矩阵右下角最大的路径，这类问题很容易联想到动态规划的思想，矩阵中到达X(i,j)的最大路径即为X(i - 1,j)与X(i,j - 1)中最大的一个加上当前grid(i,j)的值。若i为0，那么就意味着只可以从左边到达，若j为0，那么就意味着只可以从上边到达。两者都不为0时，既可以从左边到达也可以从上边到达。

代码如下：

class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] path = new int[m][n]; //用来存放最多价值礼物
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(i == 0 && j == 0){ //左上角的元素
                    path[i][j] = grid[i][j];
                    continue;
                }
                if(i == 0){//i为0，只可以从左边来
                    path[i][j] = path[i][j - 1] + grid[i][j];
                }else if(j == 0){//j为0，只可以从上边来
                    path[i][j] = path[i - 1][j] + grid[i][j];
                }else{//都不为0，可以从上边来也可以从左边来
                    path[i][j] = Math.max(path[i - 1][j],path[i][j - 1]) + grid[i][j];
                }
            }
        }
        return path[m - 1][n - 1];//返回最多价值礼物
    }
}

其中我们还可以对空间复杂度进行进一步的优化，我们寻找最大值只是与X(i - 1,j) , X(i,j - 1)和grid（i，j）有关，与grid(i - 1,j) , grid(i, j - 1)无关，因此我们可以直接再原矩阵上进行修改。