【数模】模糊综合评价模型

---

前言

模糊分布法：确定隶属度的常用方法。
模糊分布法将隶属函数看成一种 模糊分布，首先根据问题性质选取适当的模糊分布，然后再依据相关数据确定分布中的参数。

模糊分布中常用的梯形分布：

• 偏小型——一般适用于描述“小”、“浅”、“淡”等偏向小的程度的模糊现象
  
  
• 偏大型——与偏小型相反
  
  
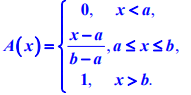
• 中间型——一般适用于描述处在 中间状态 的模糊现象
  
  
  

---

一、模糊综合评价

2005A长江水质评价与预测、2006B艾滋病疗法的评价与疗效的预测、2010B2010上海世博会影响力的定量评估

综合评价方法：
灰色评价法、层次分析法、模糊综合评价法、数据包络分析法、人工神经网络评价法、理想解法etc（可将两种评价方法集成为组合评价方法）

---

（1）基本思想

（以模糊数学为基础，应用模糊关系合成原理）
将一些 边界不清、不易定量 的因素定量化
从多个因素（多指标） 对评价事物隶属等级状况进行综合评价

（2）具体步骤

1. 确定被评价对象的因素集和评价集
2. 确定各因素权重，以及它们的隶属度向量，获得模糊评价矩阵 （如图）
3. （将模糊评价矩阵与因素的权向量）进行模糊运算并归一化

其中，第2步
确定隶属度向量——频率法

其中，第2步有两种以上的方法确定权重
①（主观）- 层次分析法
②（客观）- 根据各指标间的联系，利用数学方法计算出各指标的权重 —— 质量分数法、变异系数法（常用）

变异系数法

• 前提：所有指标在评价体系中的重要性相当

• 作用：提高指标的分辨能力，利于排序，但不能得出指标的重要程度（用变异系数法求出的某指标的权重与该指标在评价体系中的重要性是两个概念）

• 原理：敏感->大权重、不敏感->小权重

• 不适情景：当指标在评价体系中的重要性相差较大时，使用变异系数法确定权重不一定合适

若某项指标的数值差异较大，能明确区分开各被评价对象，说明该指标的分辨信息丰富，因而应给该指标以较大的权重；
反之，若各个被评价对象在某项指标上的数值差异较小，则这项指标区分各评价对象的能力较弱，因而应该给该指标较小的权重

方差——反映数据的分辨能力
其中，指标的分辨能力可定义为↓

后对 vi 进行归一化操作

（3）模糊综合评价模型的优点

1. 能够解决 所提供信息少 的问题——适用于数据不多、解决方法选择的问题
2. 对多因素、多层次的复杂问题评价效果较好（难以被其他评价方法代替）

---

二、模糊合成

1.基本思想

1. 对评价矩阵R和权向量A进行某种适当的模糊运算
2. 将两者合成为一个模糊向量B={b1,b2,……,bn}，即B=AR
3. 然后对B按照一定法则进行综合分析
4. 即可得出最终的模糊综合评价结果

2.常见算子

ps:其实也可取M为普通矩阵乘法，此时合成即为“加权平均”。至于到底取何种算子取决于 问题的性质 和 算子的特点。

主因素突出型适用于模糊矩阵中数据相差很悬殊的情形
加权平均型适用于因子很多的情形，可以避免信息丢失

---

3.获得综合评价结果

对B分析处理：
① 最大隶属度法——认定被评价对象的等级为最大隶属度对应的等级，适用于某隶属度明显大于其他隶属度的情形
② 加权平均法——

4. 获取评价矩阵R

方法（简单实用，可考虑与灰色关联分析结合使用）

1. 相对偏差（模糊矩阵评价）法
   ① 虚拟理想方案u
   ② 按照某种方法建立各方案与u的偏差矩阵R
   ③ 确定各评价指标的权重A
   ④ 用A对R加权平均 得各方案与u的综合距离F
   ⑤ 根据F对方案进行排序
   
   
   
2. 相对优属度（模糊矩阵评价）法
   ① 用适当的方法将所有指标（效益型、成本型、固定型）转化为效益型（成本型），得到优属度矩阵R
   ② 确定各评价指标的权重A
   ③ 用A对R加权平均得各方案的综合优属度F
   ④ 根据F对方案进行排序
   
   

---