在统计学和机器学习领域,概率分布是非常核心的概念,它们用于描述数据的不确定性和变化性。概率分布可以分为两大类:离散概率分布和连续概率分布。下面是一些最重要和最常见的概率分布:
离散概率分布
- 伯努利分布(Bernoulli Distribution)
- 描述的是一个只有两种可能结果的单次随机试验(例如抛硬币)。
- 二项分布(Binomial Distribution)
- 描述的是固定次数的独立重复试验中成功的次数,其中每次试验的成功概率是固定的。
- 泊松分布(Poisson Distribution)
- 用于描述在固定时间或空间内发生某事件的次数,特别适用于描述稀有事件。
- 几何分布(Geometric Distribution)
- 描述在第一次成功之前进行的独立伯努利试验次数。
- 负二项分布(Negative Binomial Distribution)
- 可以看作是几何分布的推广,描述在达到固定数量的成功之前进行的伯努利试验次数。
- 离散均匀分布(Discrete Uniform Distribution)
- 所有可能结果发生的概率都是相等的。
连续概率分布
- 正态分布(Normal Distribution)
- 也称为高斯分布,是最常见的连续概率分布之一,描述的是自然界中许多随机变量的分布情况。
- 均匀分布(Uniform Distribution)
- 在给定的范围内,任何值发生的概率是相等的。
- 指数分布(Exponential Distribution)
- 描述独立随机事件发生的时间间隔,常用于可靠性分析和排队理论。
- 伽马分布(Gamma Distribution)
- 指数分布的推广,用于描述多个独立随机事件发生的总时间。
- 贝塔分布(Beta Distribution)
- 描述在固定区间内的连续随机变量,常用于概率的概率分布。
- t-分布(t-Distribution)
- 用于小样本数据的均值分析,特别是在标准差未知的情况下。
- 卡方分布(Chi-Squared Distribution)
- 主要用于统计推断,尤其是假设检验和置信区间的估计。
- F分布(F-Distribution)
- 用于比较两个样本的方差,常用于方差分析(ANOVA)。
这些分布在统计学和机器学习中都非常重要,它们用于建模各种数据和问题,也是很多高级方法的基础。
连续数据分布
1. 正态分布(Normal Distribution)
公式定义
正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution)。若随机变量X服从一个数学期望为 μ \mu μ、方差为 σ 2 \sigma ^2 σ2的正态分布,记为 N ( μ , σ 2 ) N(\mu,\sigma^2) N(μ,σ2)。其概率密度函数为正态分布的期望值 μ \mu μ决定了其位置,其标准差 σ \sigma σ决定了分布的幅度。当 μ = 0 , σ = 1 \mu = 0,\sigma = 1 μ=0,σ=1时的正态分布是标准正态分布。 f ( x ∣ μ , σ ) = 1 σ 2 π exp ( − ( x − μ ) 2 2 σ 2 ) f(x | \mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) f(x∣μ,σ)=σ2π1exp(−2σ2(x−μ)2)其中, μ \mu μ 是均值, σ \sigma σ 是标准差。
python代码及其概率密度函数可视化
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
mu, sigma = 0, 1 # 均值和标准差
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
pdf = norm.pdf(x, mu, sigma)
plt.plot(x, pdf)
plt.title('Normal Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

2. 均匀分布(Uniform Distribution)
公式定义
也叫矩形分布,它是对称概率分布,在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数 a a a和 b b b定义,它们是数轴上的最小值和最大值,通常缩写为 U ( a , b ) U(a,b) U(a,b)。
f
(
x
∣
a
,
b
)
=
1
b
−
a
for
x
∈
[
a
,
b
]
f(x | a, b) = \frac{1}{b - a} \quad \text{for } x \in [a, b]
f(x∣a,b)=b−a1for x∈[a,b]
其中,
a
a
a 和
b
b
b 是分布的最小值和最大值。
python代码及其概率密度函数可视化
from scipy.stats import uniform
a, b = 0, 1 # 最小值和最大值
x = np.linspace(a, b, 100)
pdf = uniform.pdf(x, a, b-a)
plt.plot(x, pdf)
plt.title('Uniform Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

3. 指数分布(Exponential Distribution)
公式定义
指数分布(也称为负指数分布)是描述泊松过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。
这是伽马分布的一个特殊情况。 它是几何分布的连续模拟,它具有无记忆的关键性质。 除了用于分析泊松过程外,还可以在其他各种环境中找到。指数函数的一个重要特征是无记忆性(Memoryless Property,又称遗失记忆性)。这表示如果一个随机变量呈指数分布,当
s
,
t
>
0
s,t>0
s,t>0时有
P
(
T
>
t
+
s
∣
T
>
t
)
=
P
(
T
>
s
)
P(T>t+s|T>t)=P(T>s)
P(T>t+s∣T>t)=P(T>s)。即,如果
T
T
T是某一元件的寿命,已知元件使用了
t
t
t小时,它总共使用至少
s
+
t
s+t
s+t小时的条件概率,与从开始使用时算起它使用至少
s
s
s小时的概率相等。
f
(
x
∣
λ
)
=
λ
e
−
λ
x
for
x
≥
0
f(x | \lambda) = \lambda e^{-\lambda x} \quad \text{for } x \geq 0
f(x∣λ)=λe−λxfor x≥0
其中,
λ
\lambda
λ是率参数(事件发生的平均速率)。
python代码及其概率密度函数可视化
from scipy.stats import expon
lambda_ = 1 # 事件发生的平均速率
x = np.linspace(0, 10, 100)
pdf = expon.pdf(x, scale=1/lambda_)
plt.plot(x, pdf)
plt.title('Exponential Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

4. 伽马分布(Gamma Distribution)
公式定义
伽马分布(Gamma Distribution)是统计学的一种连续概率函数,是概率统计中一种非常重要的分布。“指数分布”和“ χ 2 \chi^2 χ2分布”都是伽马分布的特例。
假设随机变量
X
X
X为等到第
k
k
k件事发生所需的等候时间, 密度函数为
f
(
x
∣
k
,
θ
)
=
x
k
−
1
e
−
x
θ
θ
k
Γ
(
k
)
for
x
≥
0
f(x | k, \theta) = \frac{x^{k-1} e^{-\frac{x}{\theta}}}{\theta^k \Gamma(k)} \quad \text{for } x \geq 0
f(x∣k,θ)=θkΓ(k)xk−1e−θxfor x≥0
其中,
k
k
k 是形状参数,
θ
\theta
θ 是尺度参数。
伽马函数的均值和方差为 μ = k θ σ 2 = k θ 2 \mu = k \theta \\ \sigma^2 =k \theta^2 μ=kθσ2=kθ2
python代码及其概率密度函数可视化
from scipy.stats import gamma
k, theta = 2, 1 # 形状参数和尺度参数
x = np.linspace(0, 10, 100)
pdf = gamma.pdf(x, k, scale=theta)
plt.plot(x, pdf)
plt.title('Gamma Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

5. 贝塔分布(Beta Distribution)
公式定义
贝塔分布(Beta Distribution) 是一个作为伯努利分布和二项式分布的共轭先验分布的密度函数,在机器学习和数理统计学中有重要应用。Beta分布可以看做一个概率的概率分布,当你不知道一个东西的具体概率是多少时,它可以给出所有的概率出现的可能性大小
f
(
x
∣
α
,
β
)
=
x
α
−
1
(
1
−
x
)
β
−
1
B
(
α
,
β
)
for
x
∈
[
0
,
1
]
f(x | \alpha, \beta) = \frac{x^{\alpha-1} (1-x)^{\beta-1}}{B(\alpha, \beta)} \quad \text{for } x \in [0, 1]
f(x∣α,β)=B(α,β)xα−1(1−x)β−1for x∈[0,1]
其中,
α
\alpha
α 和
β
\beta
β 是形状参数,可以当做成功、失败的次数,
B
(
α
,
β
)
B(\alpha, \beta)
B(α,β) 是贝塔函数,
B
(
α
,
β
)
=
Γ
(
α
)
Γ
(
β
)
Γ
(
α
+
β
)
Γ
(
n
)
=
(
n
−
1
)
!
B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\\\Gamma(n)=(n-1)!
B(α,β)=Γ(α+β)Γ(α)Γ(β)Γ(n)=(n−1)!
python代码及其概率密度函数可视化
from scipy.stats import beta
alpha, beta_val = 2, 2 # 形状参数
x = np.linspace(0, 1, 100)
pdf = beta.pdf(x, alpha, beta_val)
plt.plot(x, pdf)
plt.title('Beta Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

6. t-分布(t-Distribution)
公式定义
t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。 t t t分布曲线形态与 n n n(确切地说与自由度 n n n)大小有关。与标准正态分布曲线相比,自由度 n n n越小, t t t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度 n n n愈大, t t t分布曲线愈接近正态分布曲线,当自由度 n = ∞ n=\infty n=∞时, t t t分布曲线为标准正态分布曲线。
假设X服从标准正态分布
N
(
0
,
1
)
\mathrm{N}(0,1)
N(0,1) ,Y服从
χ
2
(
n
)
\chi^{2}(n)
χ2(n)分布,那么
Z
=
X
Y
/
n
Z=\frac{X}{\sqrt{Y / n}}
Z=Y/nX的分布称为自由度为
n
\mathrm{n}
n的分布,记为
Z
∼
t
(
n
)
Z \sim t(n)
Z∼t(n)。分布密度函数
f
Z
(
x
∣
n
)
=
Γ
(
(
n
+
1
)
/
2
)
n
π
Γ
(
ν
/
2
)
(
1
+
x
2
n
)
−
(
n
+
1
)
/
2
f_Z(x | n) = \frac{\Gamma((n+1)/2)}{\sqrt{n\pi} \Gamma(\nu/2)} \left(1 + \frac{x^2}{n} \right)^{-(n+1)/2}
fZ(x∣n)=nπΓ(ν/2)Γ((n+1)/2)(1+nx2)−(n+1)/2
其中,
n
n
n 是自由度,
Γ
\Gamma
Γ是伽马函数。
python代码及其概率密度函数可视化
from scipy.stats import t
nu = 10 # 自由度
x = np.linspace(-5, 5, 100)
pdf = t.pdf(x, nu)
plt.plot(x, pdf)
plt.title('t-Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

7. 卡方分布(Chi-Squared Distribution)
公式定义
k
k
k个标准独立正态分布变量的平方和服从自由度为
k
k
k的卡方分布。常用于假设检验与置信区间。
f
(
x
∣
k
)
=
1
2
k
/
2
Γ
(
k
/
2
)
x
k
/
2
−
1
e
−
x
/
2
for
x
≥
0
f(x | k) = \frac{1}{2^{k/2} \Gamma(k/2)} x^{k/2 - 1} e^{-x/2} \quad \text{for } x \geq 0
f(x∣k)=2k/2Γ(k/2)1xk/2−1e−x/2for x≥0
其中,
k
k
k 是自由度。
python代码及其概率密度函数可视化
from scipy.stats import chi2
k = 2 # 自由度
x = np.linspace(0, 10, 100)
pdf = chi2.pdf(x, k)
plt.plot(x, pdf)
plt.title('Chi-Squared Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

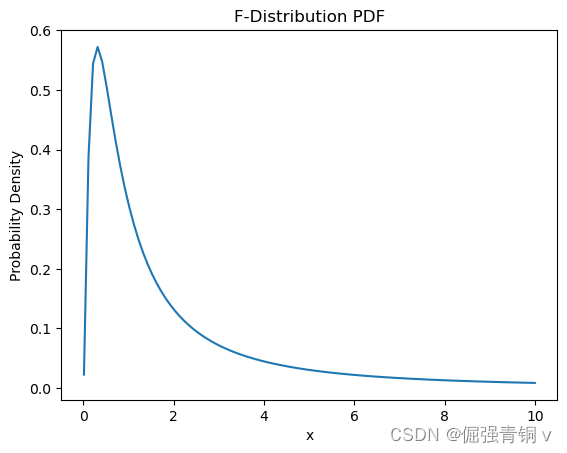
8. F分布(F-Distribution)
公式定义
f
(
x
∣
d
1
,
d
2
)
=
(
d
1
x
)
d
1
d
2
d
2
(
d
1
x
+
d
2
)
d
1
+
d
2
x
B
(
d
1
/
2
,
d
2
/
2
)
for
x
≥
0
f(x | d_1, d_2) = \frac{\sqrt{\frac{(d_1 x)^{d_1} d_2^{d_2}}{(d_1 x + d_2)^{d_1 + d_2}}}}{x B(d_1/2, d_2/2)} \quad \text{for } x \geq 0
f(x∣d1,d2)=xB(d1/2,d2/2)(d1x+d2)d1+d2(d1x)d1d2d2for x≥0
其中,
d
1
d_1
d1 和
d
2
d_2
d2 是两个独立卡方分布的自由度。
python代码及其概率密度函数可视化
from scipy.stats import f
d1, d2 = 5, 2 # 两个独立卡方分布的自由度
x = np.linspace(0.01, 10, 100) # 避免除以零
pdf = f.pdf(x, d1, d2)
plt.plot(x, pdf)
plt.title('F-Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()
离散数据分布
1. 伯努利分布(Bernoulli Distribution)
公式定义
描述的是一个只有两种可能结果的单次随机试验(例如抛硬币)。 P ( X = x ) = p x ( 1 − p ) 1 − x for x ∈ { 0 , 1 } P(X=x) = p^x(1-p)^{1-x} \quad \text{for } x \in \{0, 1\} P(X=x)=px(1−p)1−xfor x∈{0,1}
其中 p p p是事件发生的概率。
python代码及其概率分布函数可视化
import matplotlib.pyplot as plt
from scipy.stats import bernoulli
p = 0.5 # 事件发生的概率
x = [0, 1]
pmf = bernoulli.pmf(x, p)
plt.bar(x, pmf)
plt.title('Bernoulli Distribution PMF')
plt.xlabel('Outcome')
plt.ylabel('Probability')
plt.xticks(x)
plt.show()

2. 二项分布(Binomial Distribution)
公式定义
描述的是固定次数的独立重复试验中成功的次数,其中每次试验的成功概率是固定的
P
(
X
=
k
)
=
(
n
k
)
p
k
(
1
−
p
)
n
−
k
P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}
P(X=k)=(kn)pk(1−p)n−k
其中
n
n
n 是试验次数,
p
p
p 是每次试验成功的概率。
python代码及其概率分布函数可视化
from scipy.stats import binom
n, p = 10, 0.5 # 试验次数和成功概率
x = range(n+1)
pmf = binom.pmf(x, n, p)
plt.bar(x, pmf)
plt.title('Binomial Distribution PMF')
plt.xlabel('Number of Successes')
plt.ylabel('Probability')
plt.show()

3. 泊松分布(Poisson Distribution)
公式定义
用于描述在固定时间或空间内发生某事件的次数,特别适用于描述稀有事件。
P
(
X
=
k
)
=
λ
k
e
−
λ
k
!
P(X=k) = \frac{\lambda^k e^{-\lambda}}{k!}
P(X=k)=k!λke−λ
其中
λ
\lambda
λ 是单位时间(或单位面积)内平均发生的次数。
python代码及其概率分布函数可视化
from scipy.stats import poisson
lambda_ = 3 # 平均发生次数
x = range(0, 10)
pmf = poisson.pmf(x, lambda_)
plt.bar(x, pmf)
plt.title('Poisson Distribution PMF')
plt.xlabel('Number of Events')
plt.ylabel('Probability')
plt.show()

4. 几何分布(Geometric Distribution)
公式定义
描述在第一次成功之前进行的独立伯努利试验次数。
P
(
X
=
k
)
=
(
1
−
p
)
k
−
1
p
P(X=k) = (1-p)^{k-1} p
P(X=k)=(1−p)k−1p
其中
p
p
p 是每次试验成功的概率。
python代码及其概率分布函数可视化
from scipy.stats import geom
p = 0.5 # 成功概率
x = range(1, 11)
pmf = geom.pmf(x, p)
plt.bar(x, pmf)
plt.title('Geometric Distribution PMF')
plt.xlabel('Number of Trials')
plt.ylabel('Probability')
plt.show()

5. 负二项分布(Negative Binomial Distribution)
公式定义
可以看作是几何分布的推广,描述在达到固定数量的成功之前进行的伯努利试验次数。 P ( X = k ) = ( k − 1 r − 1 ) p r ( 1 − p ) k − r P(X=k) = \binom{k-1}{r-1} p^r (1-p)^{k-r} P(X=k)=(r−1k−1)pr(1−p)k−r
其中 r r r 是在停止试验前需要达到的成功次数, p p p 是每次试验成功的概率。
python代码及其概率分布函数可视化
from scipy.stats import nbinom
r, p = 5, 0.5 # 成功次数和成功概率
x = range(r, r+15)
pmf = nbinom.pmf(x, r, p)
plt.bar(x, pmf)
plt.title('Negative Binomial Distribution PMF')
plt.xlabel('Number of Trials')
plt.ylabel('Probability')
plt.show()

6. 离散均匀分布(Discrete Uniform Distribution)
公式定义
所有可能结果发生的概率都是相等的。
P
(
X
=
x
)
=
1
n
for
x
=
1
,
2
,
…
,
n
P(X=x) = \frac{1}{n} \quad \text{for } x = 1, 2, \ldots, n
P(X=x)=n1for x=1,2,…,n
其中
n
n
n是可能结果的数量。
python代码及其概率分布函数可视化
from scipy.stats import randint
low, high = 1, 7 # 最小值和最大值(不包含)
x = range(low, high)
pmf = randint.pmf(x, low, high)
plt.bar(x, pmf)
plt.title('Discrete Uniform Distribution PMF')
plt.xlabel('Outcome')
plt.ylabel('Probability')
plt.xticks(x)
plt.show()

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








