分治算法——快速排序(JAVA实现)

目录

什么是分治算法？

什么是快速排序？

代码实现

---

什么是分治算法？

分治就是指的分而治之，即将较大规模的问题分解成几个较小规模的问题，通过对较小规模问题的求解达到对整个问题的求解。

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，然后把各部分的解组合成整个问题的解。

分治算法解题步骤：分解、治理、合并。

分解：将想要解决的问题分解为若干规模较小、相互独立、与原问题形式相同的子问题。

治理：求解各个子问题。由于各个子问题与原问题形式相同，只是规模较小而已，因此当子问题划分得足够小时，就可以使用较简单的方法来解决。

合并：按原问题的要求，将子问题的解逐层合并，构成原问题的解。

分治算法有很多经典问题

二分搜索、大整数乘法、棋盘覆盖、合并排序、快速排序、线性时间选择、最接近点对问题、循环赛日程表、汉诺塔等。

本篇文章是分治算法的快速排序问题。

什么是快速排序？

快速排序：又称划分交换排序（partition-exchange sort），简称快排，一种排序算法，最早由东尼·霍尔提出。在平均状况下，排序n个项目要O(n log2 n)（大O符号）次比较。在最坏状况下则需要 O(n^2)次比较，但这种状况并不常见。事实上，快速排序 (n log n)通常明显比其他算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地达成。——（维基百科）

简单来说：就是给基准值找正确位置的过程。

每一趟选择当前所有子序列中的一个关键字（通常是第一个）作为基准值，将子序列中比基准值小的放到基准值的左边， 比基准值大的放到基准值的右边；以后采用递归的方式分别对前半部分和后半部分排序，当前半部分和后半部分均有序时该数组就自然有序了。

具体分析： 

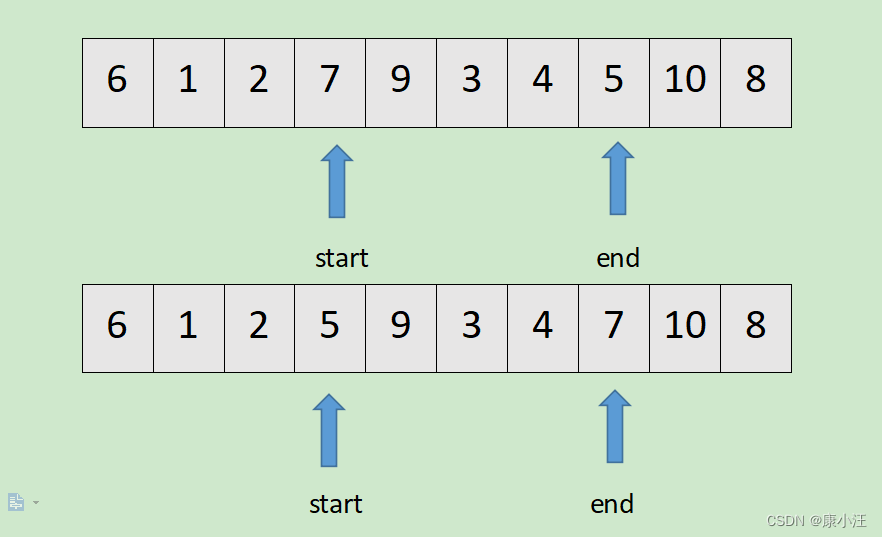
如下图所示，将数组的第一个元素作为基准数，首先用一个临时变量存储基准数，然后从数组的两端扫描数组，start指向起始位置，end指向末尾位置。

首先用end扫描数组，如果end指向的值小于基准数，继续用start扫描数组，否则执行end-1，直到end指向的值小于基准数。

用start扫描数组，如果start指向的值大于基准数，将end指向的值和start指向的值互换。否则执行statr+1，直到start指向的值大于基准数。最后将end指向的值和start指向的值互换。

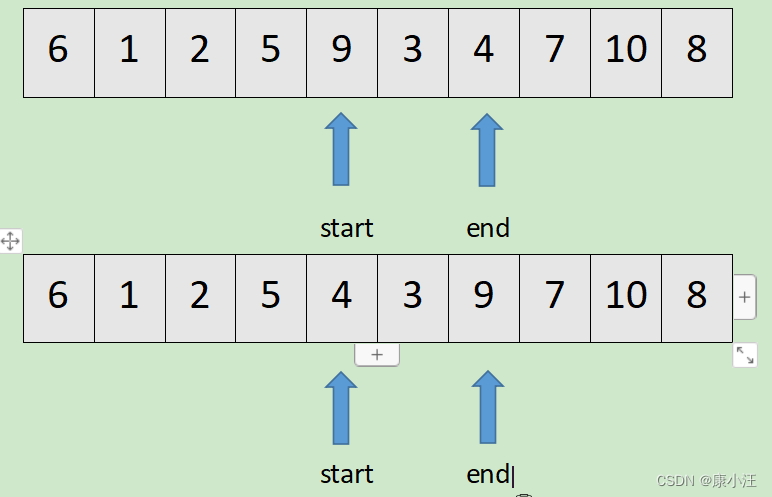
当start和end指向同一个位置时，执行基准数归位。就是将数组第一个元素与start或end此时指向的元素互换。此时，基准数左边的数都它小，基准数右边的数都比它大。

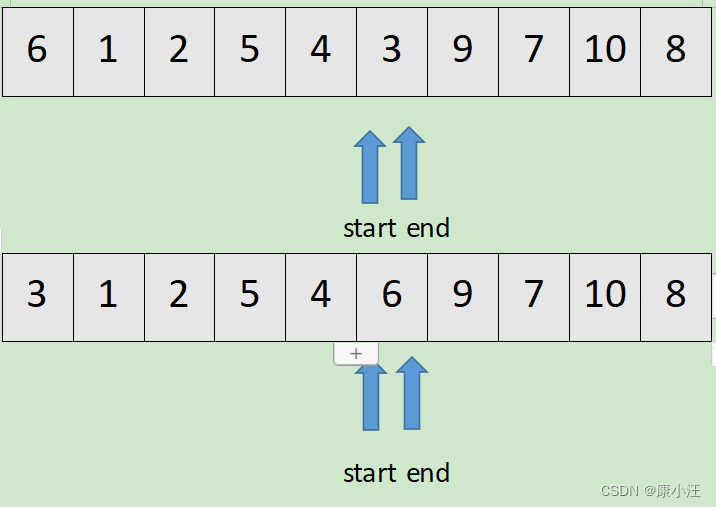
  最后采用递归的方式一直分别对前半部分和后半部分排序，当所有的前半部分和后半部分均有序时该数组就自然有序了。

代码实现

public static void paixu(int[] arr, int i,int j){

        //定义两个变量用来记录查找范围
        int start = i;
        int end = j;
        if (start>end){
            return;
        }
        //记录基准数
        int baseNumber = arr[i];
        //利用循环找出要交换的数
        while(start != end){
            //利用end从后往前找比基准数小的数，这里必须先从end开始！！！
            while(true){
                if (end<=start || arr[end]<baseNumber){
                    break;
                }
                end--;
            }
            //利用start从前往后找比基准数大的数
            while (true){
                if (end<=start || arr[start]>baseNumber) {
                    break;
                }
                start++;
            }
            //将end和start指向的数进行交换
            int temp = arr[start];
            arr[start] = arr[end];
            arr[end] = temp;

        }
        //基准数归位
        int temp = arr[i];
        arr[i]= arr[start];
        arr[start]=temp;
        //确定基准数左边的范围，递归
        paixu(arr,i,start-1);
        //确定基准数右边的范围，递归
        paixu(arr,start+1,j);

    }