本文介绍了Dijkstra算法在找到最短路径后的回溯方法。通过记录每个节点更新距离时的前驱节点，可以从目标节点反向追踪，找出从起点到目标的最短路径。具体步骤包括查看相关资源，理解算法原理，并通过实例展示了从点A到点G的回溯过程，得出最短路径为A->C->D->E->G。
主要把原文里的内容做了个介绍…
转载内容
大部分国内资料和讲解都没太讲完整。一个路径规划算法，翻来覆去地讲怎么改变每个节点距离起点的距离值，却讲不清楚更新完每个节点的值以后怎么寻找最短路径的。
按照下面步骤来看就行了：
1，先看这个(原po的链接挂了我随便换一个，有知道原文章是哪篇的可以给一下~)，这个虽然没讲怎么找路径，但怎么更新每个节点的值（即与起点的距离）这方面它讲得比较清晰。
2，看完1之后，看这个（要翻墙），包含了1里面的步骤，同时讲了怎么找到最短路径的。总结就是一句话：每个节点改变值的时候，同时会记录：“从哪个节点走到它路径更短，使得它的值改变了”。这样就能从目标节点反向跟踪前面的节点，找到路径。
原文链接：https://blog.youkuaiyun.com/ethan_guo/article/details/82419216
需要翻墙的视频内容
假如给定的无向图如上，我们从A起始，那么得到的Dijkstra算法的过程如下：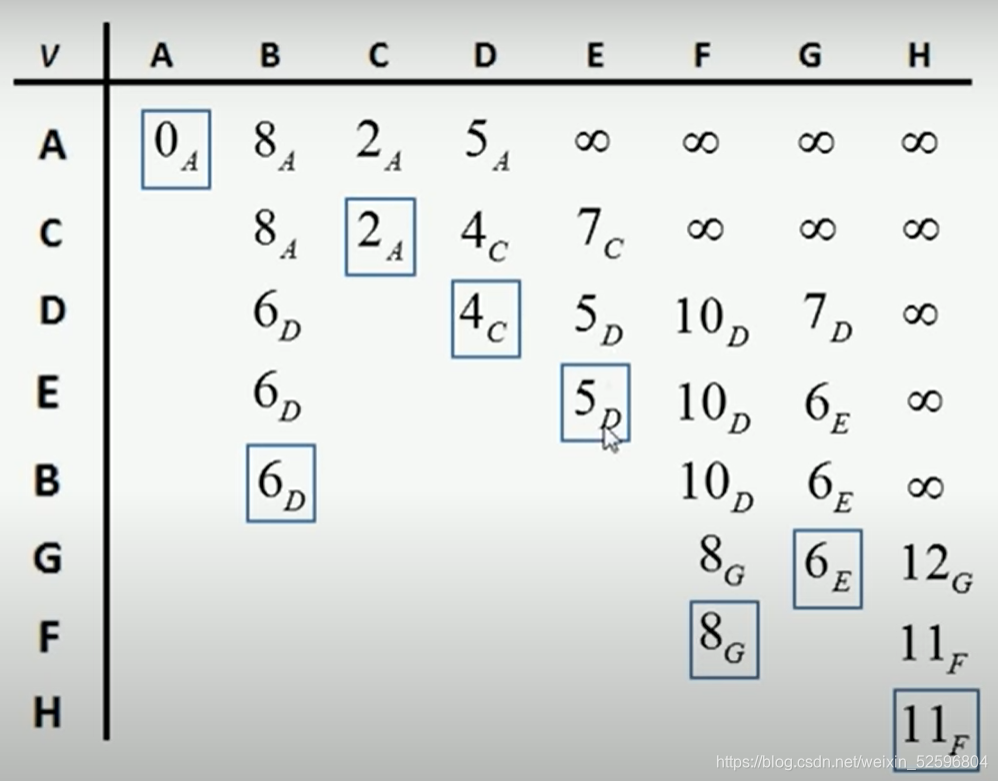
如果我们需要知道从点A到点G的最短路径，那就向前“回溯”
最低0.47元/天 解锁文章
扫一扫
659
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
