浅谈哈希表

散列表 （ Hash table ，也叫 哈希表 ），是根据 键 （Key）而直接访问在记忆体储存位置的 数据结构 。也就是说，它通过计算一个关于键值的函数，将所需查询的数据 映射 到表中一个位置来访问记录，这加快了查找速度。

哈希表本质上是个数组

哈希函数的构造

哈希表的构造一般有直接定址法，数字分析法，平方取中法，折叠法，随机数法和除留余数法。

直接定址法：
存储位置 = Map(key) = a*key+b(a,b为常数)
优点：简单、均匀，也不会产生冲突，但问题是这需要事先知道关键字的分布情况，适合查找表较小且连续的情况

数字分析法：
分析关键字的特点，选取关键字的一部分来计算散列存储位置的方法。数字分析法，通常适合处理关键字位数比较大的情况，如果事先知道关键字的分布且关键字的若干位分布较均匀。

平方取中法：
假设关键字是1234，那么它的平方就是1522756，再抽取中的3位就是227，用作散列地址。平方取中法比较适合于不知道关键字的分布，而位数又不是很大的情况。

折叠法：
将关键字分割成位数相同的几部分（最后一部分的位数可以不同），然后取这几部分的叠加和（舍去进位）

随机数法：
存储位置 = Map(key) = random(key)( random() 是随机函数 )

除留余数法：
存储位置 = Map(key) = key mod p( p ≤ m , m 为散列表长 )

哈希冲突

如果数据庞大或者因为哈希哈函数构造的不好，容易出现两个数哈希成同一个值，这就是哈希冲突。

处理哈希冲突

介绍两种主要的方法，一个是开放寻址法，一个是拉链法。笔者会在例题中展示。

例题

模拟散列表

维护一个集合，支持如下几种操作：

I x，插入一个数 x；
Q x，询问数 x 是否在集合中出现过；
现在要进行 N 次操作，对于每个询问操作输出对应的结果。

输入格式
第一行包含整数 N，表示操作数量。

接下来 N 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。

输出格式
对于每个询问指令 Q x，输出一个询问结果，如果 x 在集合中出现过，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围
1≤N≤105
−109≤x≤109

输入样例：
5
I 1
I 2
I 3
Q 2
Q 5

输出样例：
Yes
No

开放寻址法

#include <iostream>
#include <cstring>
using namespace std;
const int N = 300010,null = 0x3f3f3f3f;
int h[N];
int find(int x)
{
    int t = (x % N + N) % N; // c++中如果是负数那他取模也是负的所以加N再%N就一定是一个正数
    while(h[t] != null && h[t] != x) //如果该位子有用过，找下一个
    {
        t ++;
        if(t == N)
        t = 0;
    }
    return t;    //返回 t 该在的位子
}
int main()
{
    int n;
    cin >> n;
    memset(h,0x3f,sizeof h);
    while(n --)
    {
        string s;
        int x;
        cin >> s >> x;
        if(s == "I") h[find(x)] = x;
        else 
        {
            if(h[find(x)] == null) puts("No");
            else puts("Yes");
        }
    }
    return 0;
}

拉链法

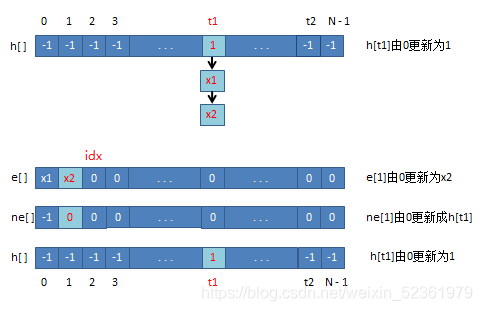
#include <cstring>
#include <iostream>

using namespace std;

const int N = 100003;

int h[N], e[N], ne[N], idx;

void insert(int x)
{
    int k = (x % N + N) % N;
    e[idx] = x;
    ne[idx] = h[k];
    h[k] = idx ++ ;
}

bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; i != -1; i = ne[i])
        if (e[i] == x)
            return true;

    return false;
}

int main()
{
    int n;
    scanf("%d", &n);

    memset(h, -1, sizeof h);

    while (n -- )
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);

        if (*op == 'I') insert(x);
        else
        {
            if (find(x)) puts("Yes");
            else puts("No");
        }
    }

    return 0;
}

字符串哈希

给定一个长度为 n 的字符串，再给定 m 个询问，每个询问包含四个整数 l1,r1,l2,r2，请你判断 [l1,r1] 和 [l2,r2] 这两个区间所包含的字符串子串是否完全相同。

字符串中只包含大小写英文字母和数字。

输入格式
第一行包含整数 n 和 m，表示字符串长度和询问次数。

第二行包含一个长度为 n 的字符串，字符串中只包含大小写英文字母和数字。

接下来 m 行，每行包含四个整数 l1,r1,l2,r2，表示一次询问所涉及的两个区间。

注意，字符串的位置从 1 开始编号。

输出格式
对于每个询问输出一个结果，如果两个字符串子串完全相同则输出 Yes，否则输出 No。

每个结果占一行。

数据范围
1≤n,m≤105

输入样例：
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2

输出样例：
Yes
No
Yes

思路：

#include<iostream>
#include<cstring>
using namespace std;
const int N = 200003,null = 0x3f3f3f3f,P = 131;
char str[N];
int p[N],h[N];
int get(int l,int r)
{
    return h[r] - h[l-1] * p[r - l + 1];
}
int main()
{
    memset(h,0x3f,sizeof h);
    int n,m;
    cin >> n >> m;
    cin >> str + 1;
    
    p[0] = 1;
    for(int i = 1; i <= n; i ++) 
    {
        h[i] = h[i-1] * P + str[i];
        p[i] = p[i-1] * P;
    }
    while(m --)
    {
        int l1,r1,l2,r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if(get(l1,r1) == get(l2,r2)) puts("Yes");
        else puts("No");
    }
    return 0;
}