Tire 树运用

什么是Trie树

在 计算机科学 中， trie ，又称 前缀树 或 字典樹 ，是一种有序 树 ，用于保存 关联数组 ，其中的键通常是 字符串 。. 与 二叉查找树 不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的 前缀 ，也就是这个节点对应的字符串，而根节点对应 空字符串 。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。
[百度百科]

结构如下：

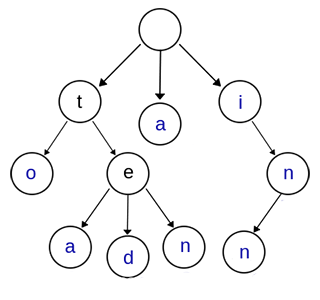
基本性质：
根节点不包含字符，除根节点外的每一个子节点都包含一个字符。
从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
每个节点的所有子节点包含的字符互不相同。

Trie树的优缺点

Trie树的核心思想是空间换时间，利用字符串的公共前缀来减少无谓的字符串比较以达到提高查询效率的目的。

优点

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

Trie树可以对关键字按字典序排序。

缺点

空间消耗比较大。

运用

一、插入与查询

Trie字符串统计

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 x；
Q x 询问一个字符串在集合中出现了多少次。
共有 N 个操作，输入的字符串总长度不超过 105，字符串仅包含小写英文字母。

输入格式
第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式
对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围
1≤N≤2∗104

输入样例：
5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：
1
0
1

#include<iostream>
using namespace std;
const int N = 100010;
int son[N][26],cnt[N],idx;
char str[N];

void insert(char *str)
{
    int p = 0;
    for(int i = 0; str[i]; i ++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++;
}
int query(char *str)
{
    int p = 0;
    for(int i = 0; str[i]; i ++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;
        p = son[p][u];
    }
    return cnt[p];
}

int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        char op[2];
        cin >> op >> str;
        if(*op == 'I') insert(str);
        else cout << query(str) << endl;
    }
    return 0;
}

二、词频统计

前缀统计

给定 N 个字符串 S1,S2…SN，接下来进行 M 次询问，每次询问给定一个字符串 T，求 S1∼SN 中有多少个字符串是 T 的前缀。

输入字符串的总长度不超过 106，仅包含小写字母。

输入格式
第一行输入两个整数 N，M。

接下来 N 行每行输入一个字符串 Si。

接下来 M 行每行一个字符串 T 用以询问。

输出格式
对于每个询问，输出一个整数表示答案。

每个答案占一行。

输入样例：
3 2
ab
bc
abc
abc
efg

输出样例：
2
0

理解 Trie 树的构造这题很容易想到，只要把出现的节点次数加起来

#include<iostream>
using namespace std;
const int N = 100010;
int son[N][26],cnt[N],idx;
char str[N];

void insert(char *str)
{
    int p = 0;
    for(int i = 0; str[i]; i ++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) son[p][u] = ++ idx;
        p = son[p][u];
    }
    cnt[p] ++;
}

int query(char *str)
{
    int p = 0,ans = 0;
    for(int i = 0; str[i]; i ++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return ans;
        p = son[p][u];
        ans += cnt[p];
    }
    return ans;
}

int main()
{
    int n,m;
    cin >> n >> m;
    while(n --)
    {
        cin >> str;
        insert(str);
    }
    while(m --) 
    {
        cin >> str;
        cout << query(str) << endl;
    }
    return 0;
}

电话列表

给出一个电话列表，如果列表中存在其中一个号码是另一个号码的前缀这一情况，那么就称这个电话列表是不兼容的。

假设电话列表如下：

Emergency 911
Alice 97 625 999
Bob 91 12 54 26

在此例中，报警电话号码（911）为 Bob 电话号码（91 12 54 26）的前缀，所以该列表不兼容。

输入格式
第一行输入整数 t，表示测试用例数量。

对于每个测试用例，第一行输入整数 n，表示电话号码数量。

接下来 n 行，每行输入一个电话号码，号码内数字之间无空格，电话号码不超过 10 位。

输出格式
对于每个测试用例，如果电话列表兼容，则输出 YES。

否则，输出 NO。

数据范围
1≤t≤40,
1≤n≤10000

输入样例：
2
3
911
97625999
91125426
5
113
12340
123440
12345
98346

输出样例：
NO
YES

思路：
判断是否存在一个串是当前串的前缀；当前串是否是某串的前缀

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n;
int son[N][10], idx;
bool f[N];

bool insert(char *str)
{
    int p = 0;
    bool has_new = false;
    bool has_found = false;
    for (int i = 0; str[i]; i ++ )
    {
        int u = str[i] - '0';
        if (!son[p][u])
        {
            son[p][u] = ++ idx;
            has_new = true;
        }
        p = son[p][u];
        if (f[p]) has_found = true;
    }

    f[p] = true;

    return has_new && !has_found;
}

int main()
{
    int T;
    cin >> T;
    while (T -- )
    {
        cin >> n;
        memset(son, 0, sizeof son);
        memset(f, false, sizeof f);
        idx = 0;

        bool res = true;

        char str[20];
        for (int i = 0; i < n; i ++ )
        {
            cin >> str;
            if (!insert(str)) res = false;
        }

        if (res) puts("YES");
        else puts("NO");
    }

    return 0;
}

三、删除

删除节点的情况有3种情况：

1、待删除的单词是另一个单词的前缀

把该单词的最后一个节点的标记去掉，cnt[p]--;

2、待删除的单词的所有字母都没有多个分支，删除整个单词
将该单词首个 son[p][u]初始化为0

3、待删除的单词的除了最后一个字母，其他的字母有多个分支
把该单词的最后一个节点的标记去掉，cnt[p]--;

关于Trie 树的后缀树和AC自动机后续会进行补充。

欢迎点赞与评论~