LeetCode-142

142. 环形链表 IIhttps://leetcode-cn.com/problems/linked-list-cycle-ii/

难度中等

给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意，pos 仅仅是用于标识环的情况，并不会作为参数传递到函数中。

说明：不允许修改给定的链表。

进阶：

• 你是否可以使用 O(1) 空间解决此题？

示例 1：

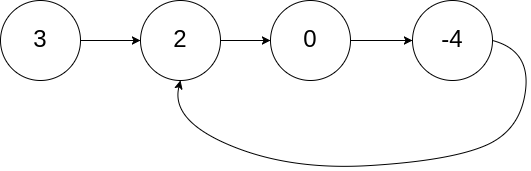
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引

题解：

此题解来源于代码启示录

思路分析

第一 首先要确定是否有环

第二 要确定在哪里相遇

对于第一点的求解 用了快慢指针法 fast指针每次走两步  slow指针每次走一步 如果他们能遇到说明可以构成环 如果遇不到说明构成不了环 很好理解 就跟高中时 行星公转多一圈一样 快的周期小的总比慢的多走一圈

对于第二点的求解

图源代码启示录

两者相遇 slow走过的结点数是x+y  fast走过的结点数是(x+y)+(n)(y+z)

根据数学关系 fast走过的结点数一定是slow走过的结点数的二倍

所以2*(x+y)=(x+y)+n*(y+z)

合并同类项得  （x+y)=n*(y+z)

x=(n-1)*(y+z) +z

当n=1时 得x=z

即重新定义两个指针一个从头结点走 一个从相遇处走 速度一致 当他们相遇时 即是环的出口

当n=2或者更大时

一样的只是多走了几圈 可以画图

所以代码如下

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode*fast=head;
        ListNode*slow=head;
        while(fast!=NULL&&fast->next!=NULL){
            fast=fast->next->next;
            slow=slow->next;
            if(slow==fast){
                ListNode*temp1=slow;
                ListNode*temp2=head;
                while(temp1!=temp2){
                    temp1=temp1->next;
                    temp2=temp2->next;
                }
                return temp2;
            }
            
        }
        return NULL;
    }
};

他亦无它 唯他手熟尔 加油！