dagum基尼系数分解工具

dagum基尼系数分解工具

相比于传统的基尼系数而言，Dagum 基尼系数能够将其分解为地区内差距、地区间差距以及超变密度。

Dagum基尼系数的相关计算公式如下：

1、总体基尼系数：

2.子群内部基尼系数

3.子群之间基尼系数 

4.子群内差异对总体基尼系数贡献

5.子群间差异对总体基尼系数的贡献 

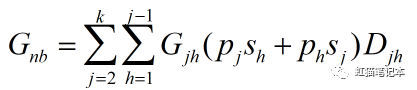
6.超变密度的贡献 

 网上目前计算dagum基尼系数分解的方法，一般是matlab代码，该方法要求首先要把数据按子群划分为不同的列，同时要把列按照平均值从大到小的顺序依次排列，且每次只能计算一年的数据，有些则对分组有限制，只能分解固定子群数的数据，同时输出的数据并非excel，还需要二次整理，很不方便。有鉴于此，我编写了一个自动化的脚本，主要特点如下：

1、无须使用者安装任何R、matlab软件，完全无代码操作。

2.对子群数没有限制，2组及以上均可。

3.可以同时计算一年或者多年的dagum基尼系数分解结果，自动化输出。

4.所有相关参数，一应俱全。

使用方法如下：

1、将数据按如下格式排列，第一列命名为“year”，为年份，第二列为“data”，为要计算的数据，第三列为“tag”，为子群分组标签，然后数据保存为“data.xlsx”，放到D盘根目录，打开程序。

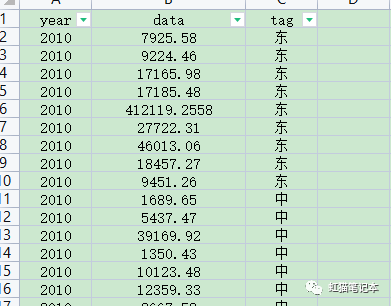
2、稍等片刻，程序会出现如下截图中的内容，说明程序已运行完成，在D盘根目录会生成名为“dagum基尼系数分解结果.xlsx”的文件，打开即可。

3.输出文件结果如下图所示

 从左到右，依次是年份、总体基尼系数，子群内差异对总体基尼系数的贡献、子群间差异对总体基尼系数的贡献、超变密度的贡献，子群内差异贡献率、子群间差异贡献率、超变密度贡献率，G_sub是各子群的基尼系数，G_jh是子群间基尼系数。

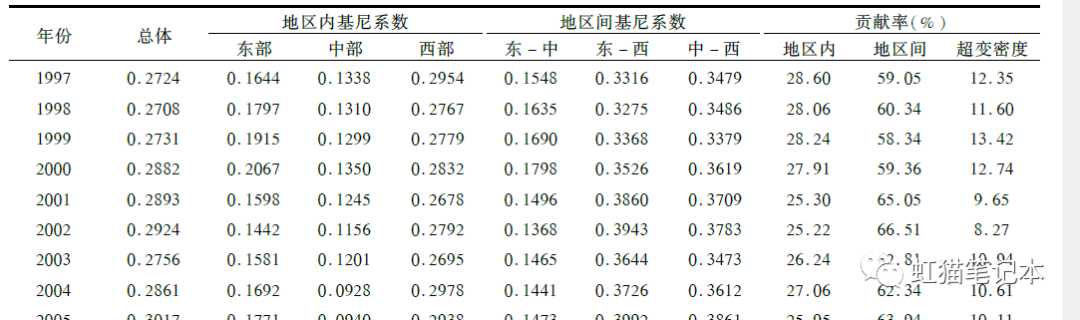
可以看到与文献中所使用的结果形式基本相同，可以直接放进论文中即可。

参考文献：我国财政医疗卫生支出的空间差异及分布动态演进（李强谊， 钟水映）

 获取方式：1、访问工具视界官网：dagum基尼系数分解工具 - 工具视界

2、关注公众号“工具视界”，后台回复 dagum，获取该工具。