机器学习-总结笔记-贝叶斯学习

最新推荐文章于 2024-08-13 17:57:37 发布

Toooooopia

最新推荐文章于 2024-08-13 17:57:37 发布

阅读量599

点赞数 1

分类专栏：机器学习文章标签：机器学习

本文链接：https://blog.youkuaiyun.com/weixin_52329576/article/details/115246827

版权

机器学习专栏收录该内容

5 篇文章

订阅专栏

本文详细探讨了贝叶斯学习方法，包括其特性、困难、贝叶斯法则、先验后验概念，以及朴素贝叶斯分类器的原理与评价。重点讲解了贝叶斯公式在决策制定中的作用和MAP假定，以及如何通过朴素贝叶斯解决数据稀疏问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本文为自学西瓜书和学校课堂整理笔记。

导论

在这里插入图片描述

贝叶斯学习

贝叶斯学习方法特性

观察到的每个训练样例可以增量地降低或升高某假设的估计概率。
先验知识可以与观察数据一起决定假设的最终概率。
可允许假设做出不确定性的预测；先验。
新的实例分类可由多个假设一起做出预测，用它们的概率来加权。

贝叶斯学习方法困难

需要概率的初始知识，当概率预先未知时，可以基于背景知识、预先准备好的数据以及基准分布的假定来估计这些概率。
一般情况下，确定贝叶斯最优假设的计算代价比较大（在某些特定情形下，这种计算代价可以大大降低）。

贝叶斯法则

贝叶斯判定准则

只需在每个样本上选择那个能使条件风险 P(h|D)最小的类别标记即可获得总体风险的最小化。
在这里插入图片描述
此时，h* 称为贝叶斯最优分类器，与之对应的总体风险 R(h*)称为贝叶斯风险，1- R(h*)反映了分类器所能达到的最好性能。

先验概率 & 后验概率 & 似然度

先验概率
当一个训练集中包含充足的独立同分布样本时，可以采用大数定律，将各类样本出现的频率估计对应的先验概率。
P(h)：h的先验概率。
用P(h)表示在没有训练数据前假设h拥有的初始概率；如果没有这一先验知识，可以简单地将每一候选假设赋予相同的先验概率（均匀分布、最大熵）
P(D)表示训练数据D的先验概率。
数据先验概率不太关注，因为数据已经发生，和模型关联不大
后验概率
P(h|D)：即给定D时h的成立的概率，称为h的后验概率
用数据估计某种特定的模型的概率比较低/难；应该尤为关注这个！！！
似然度
P(D|h)表示假设h成立时D的概率，称为似然/生成概率
数据和模型之间的似然度；likelihood；模型生成数据的可能性

贝叶斯公式

在这里插入图片描述
如果D独立于h时被观察到的可能性越大，那么D对h的支持度越小。
P.S. Loss：-logP(h|D)——负对数似然；越小越好

极大后验假设 MAP

MAP：学习器在候选假设集合H中寻找给定数据D时可能性最大的假设h。
在这里插入图片描述
在最后一步中，发现把P(D)去掉了，这是因为P(D)是一个不依赖于h的常量；而且若对模型一无所知，就可以视作为均匀分布，那P(h)也可去掉。

假定

训练数据D是无噪声的，即di=c(xi)
目标概念c包含在假设空间H中
每个假设的概率相同

可推出

前面说了，若不了解h的分布情况，可视作均匀分布，那么P(h) = 1 / |H|。
由于训练数据无噪声，那么给定假设h时，与h一致的D的概率为1，不一致的概率为0。
so，P(h|D) 的情况应为：
h与D不一致时：

h与D一致时：
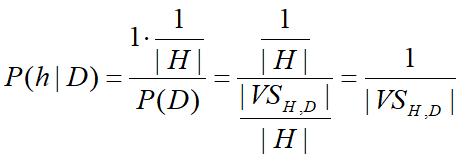
在这里插入图片描述
注： VS是关于D的变型空间（即与D一致的假设集）；后验概率就是变型空间里所有假设的均匀分布的结果。

推导出P(D):

极大似然估计 Maximum Likelihood Estimation，MLE

使P(D|h)最大的假设被称为极大似然假设。

在这里插入图片描述

贝叶斯推理举例

这个例子很像学概率论时的数学题吼。
针对化验检测是否生病的情况：

已知：
P(disease)=0.008, P(well)=0.992
P(+|disease)=0.98, P(-|disease)=0.02
P(+|well)=0.03, P(-|well)=0.97
化验诊断效果如何？
P(+|disease)P(disease)=0.0078
P(+|well)P(well)=0.0298
P(disease|+)=0.0078/(0.0078+0.0298)=0.21
P(well|+)=0.79

贝叶斯推理的结果很大程度上依赖于先验概率，另外不是完全接受或拒绝假设，只是在观察到较多的数据后增大或减小了假设的可能性。

朴素贝叶斯分类器

根据贝叶斯公式来看
P(D|h)是所有属性上的联合概率，难以从有限的训练样本直接估计而得。
贝叶斯方法的新实例分类目标是在给定描述实例的属性值<a1,…,an>下，得到最可能的目标值V

估计P(vj)很容易，计算每个目标值vj出现在训练数据中的频率；但是P(a1…an|vj)往往很小，很不好计算；且训练的时候出现概率很低，极有可能测试的时候概率为0——数据稀疏问题（除非有一个非常大的训练数据集，否则无法获得可靠的估计）。
因此，朴素贝叶斯分类器采用了属性条件独立性假设：对于已知类别，假设所有属性相互独立；即假设每个属性独立对分类结果发生影响。
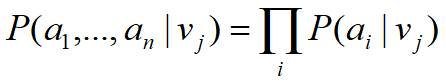
朴素贝叶斯分类器的表达式：

注：因为P(a1,a2,…,an)对于所有类别来说都是相同的。
接下来，拆解一下朴素贝叶斯分类器的表达式：
1、 P(vj)

2、 P(ai|vj)
（1）连续属性：

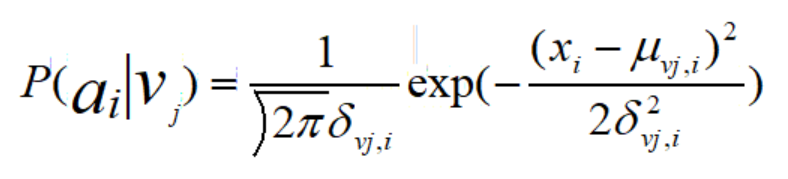
（2）离散属性：

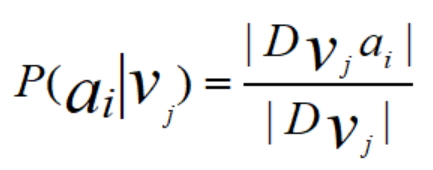
3、注意：可能某个属性值在数据集中从未出现过，为了避免其的概率值为0，可以采用“平滑”方式。
常用拉普拉斯修正：N表示D中可能出现的类别数，Ni是指第 i 个属性可能的取值数。

朴素贝叶斯分类器评价

从训练数据中估计不同P(ai|vj)项的数量比要估计P(a1,…,an|vj)项所需的量小得多
朴素贝叶斯分类器的训练过程就是基于训练集D来估计先验概率P(vj) & 每个属性的条件概率P(ai|vj)
朴素贝叶斯分类器与其他已介绍的学习方法的一个区别：没有明确地搜索可能假设空间的过程（假设的形成不需要搜索，只是简单地计算训练样例中不同数据组合的出现频率）