杭电第六场

Yes, Prime Minister

题意
给我们一个数字，这个数字在一个连续的区间内，这个区间内所有的数字之和是一个质数，要求我们求出这样的最短的区间；
题解
其实对于这道题我们会发现，其实它是一定有一个区间，区间内所有数之和是一个质数，（证明等会儿讲）
首先，怎样长度的区间才会出现区间和是一个质数呢（先考虑正整数）
其实只有当长度为一和为二的时候才会出现，当长度大于二的时候是一定不会出现质数的，这个东西我们可以打表看一下，从n开始
长度为三的时候是3n+3，四的时候是4n+6，五的时候是5n+10，六的时候是6n+15，都是有公因子的；
当它为负数的时候，我们就可以先把它变成正数，然后按照这个递推下去；
但是当长度为一和二的时候都不是质数的时候呢，没有了吗，其实不是的，我们可以先把它归零，然后递推下去
因为这个区间可以两边扩展，所以我们是可以讲它向两边扩展，直到找到满足条件的数
所以我们可以看出，每一个数都是有一个区间满足区间之和是一个质数的；

//#define _ 0
//return ~~(0^_^0)~~
#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>
using namespace std;
#define int long long
const int N = 3e7+100;
int primes[N], cnt=0;     // primes[]存储所有素数
bool st[N],f[N];         // st[x]存储x是否被筛掉

void get_primes(int n)
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) primes[cnt++] = i;
        for (int j = 0; primes[j] <= n / i; j++)
        {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}
void solve() {
	int n;
	cin >> n;
    if (n == 0) {
        cout << 3 << endl;
    }
    else if (n > 0) {
        if (f[n])cout << 1 << endl;
        else if (f[n + n + 1] || f[n + n - 1])cout << 2 << endl;
        else {
            int ans = 2 * n + 1;
            n++;
            while (!f[n + n + 1]&&!f[n]) {
                n++;
                ans += 2;
            }
            if (f[n])ans += 1;
            else ans += 2;
            cout << ans << endl;
        }
    }
    else {
        int ans = 2 * abs(n) + 1;
        n = abs(n) + 1;
        if (f[n]) {
            cout << (ans + 1) << endl;
        }
        else if (f[n + 1 + n])cout << (ans + 2) << endl;
        else {
            while (!f[n + n + 1] && !f[n]) {
                n++;
                ans += 2;
            }
            if (f[n])ans += 1;
            else ans += 2;
            cout << ans << endl;
        }
    }
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int T;
    get_primes(N);
    for (int i = 0; i < cnt; i++) {
        f[primes[i]] = 1;
    }
	cin >> T;
	while (T--)solve();
}

Median

题意
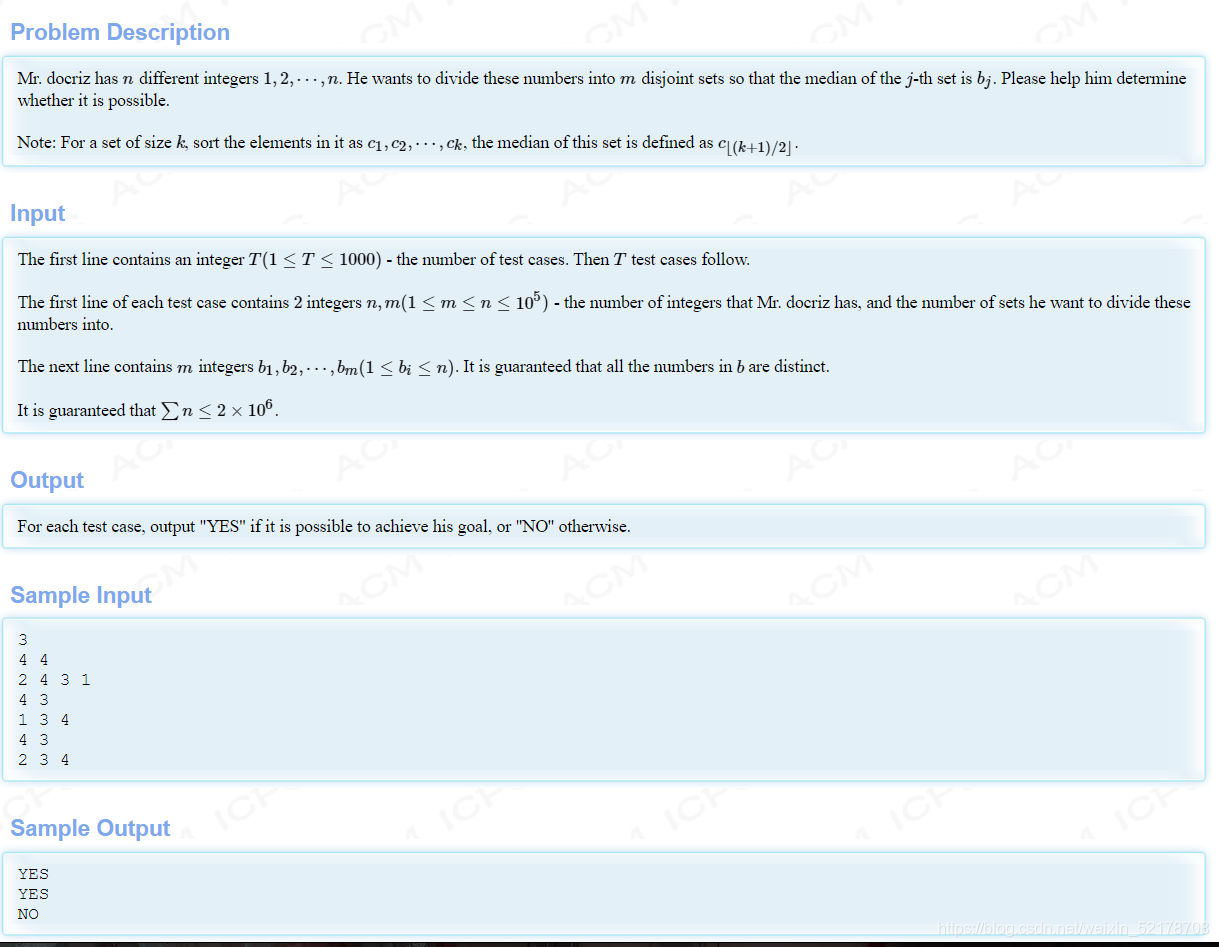
一个长度为n的数组，其中有m个数，构造m个区间，每一个区间的中位数都是给定的数
题解
所以我们可以在数轴上讲m以此标出来，我们会发现，每一段若不连续都会构成一个区间，可以发现，不在同一个区间的两个点是可以相互抵消的
所以，当没有区间大于其他区间之和时，就会全部抵消或者是剩一个，这个时候我们是一定可以构造的；
但是，当出现区间大于其他区间之和时，我们就要全力讲这个区间化小，最后剩下的数就是(2*max-sum),我们可以发现，当区间长度为二时，所得到的区间中位数是前一个数，所以如果有多余的，我们可以将多余的分别于小于等于区间最小值的进行匹配，也就是说，当剩下的数量小于等于集合(值小于等于区间最小值）中的数的个数时也是可以构造出的，但是大于的时候就不行了

#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>
using namespace std;
#define int long long
#define _ 0

void solve() {
	int n, m;
	cin >> n >> m;
	vector<int>a(m + 1);
	int maxn = 0, maxt = 0, sum = 0;
	for (int i = 1; i <= m; i++)cin >> a[i];
	sort(a.begin(), a.end());
	for (int i = 1; i <= m; i++) {
		int tmp = a[i] - a[i - 1] - 1;
		if (tmp > maxn) {
			maxn = tmp;
			maxt = i;
		}
		sum += tmp;
	}
	if (a[m] != n) {
		int tmp = n - a[m] - 1;
		sum += tmp;
		if (tmp > maxn) {
			maxn = tmp;
			maxt = m;
		}
	}
	if ((2 * maxn - sum) <= (maxt - 1) || sum == 0) cout << "YES" << endl;
	else cout << "NO" << endl;
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int T;
	cin >> T;
	while (T--)solve();
	return ~~(0 ^ _ ^ 0);
}