杭电第五场

VC Is All You Need

//#define _ 0
//return ~~(0^_^0)~~
#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>

using namespace std;
#define ll long long 
void solve() {
	long long n, m;
	cin >> n >> m;
	if (n >= m + 2)cout << "No" << endl;
	else cout << "Yes" << endl;
}

signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int t;
	cin >> t;
	while (t--)solve();
}

Cut tree

按照题意模拟即可

//#define _ 0
//return ~~(0^_^0)~~
#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>

using namespace std;
#define ll long long
const int N = 1000010;
struct segment {
	int a[3];
}t[N<<2];
int n, cnt, x;
void build(int x, int l, int r) {
	if (l == r)return;
	if (r == l + 1) {
		build(t[x].a[0] = ++cnt, l, l);
		build(t[x].a[1] = ++cnt, r, r);
		return;
	}
	int len = (r - l) / 3 + 1;
	int a = l + len - 1, b = a + r >> 1;
	build(t[x].a[0] = ++cnt, l, a);
	build(t[x].a[1] = ++cnt, a + 1, b);
	build(t[x].a[2] = ++cnt, b + 1, r);
}
void solve() {
	cnt = 1;
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> x;
	build(1, 1, n);
	cout << cnt << endl;
}

signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int T;
	cin >> T;
	while (T--)solve();
}

Banzhuan

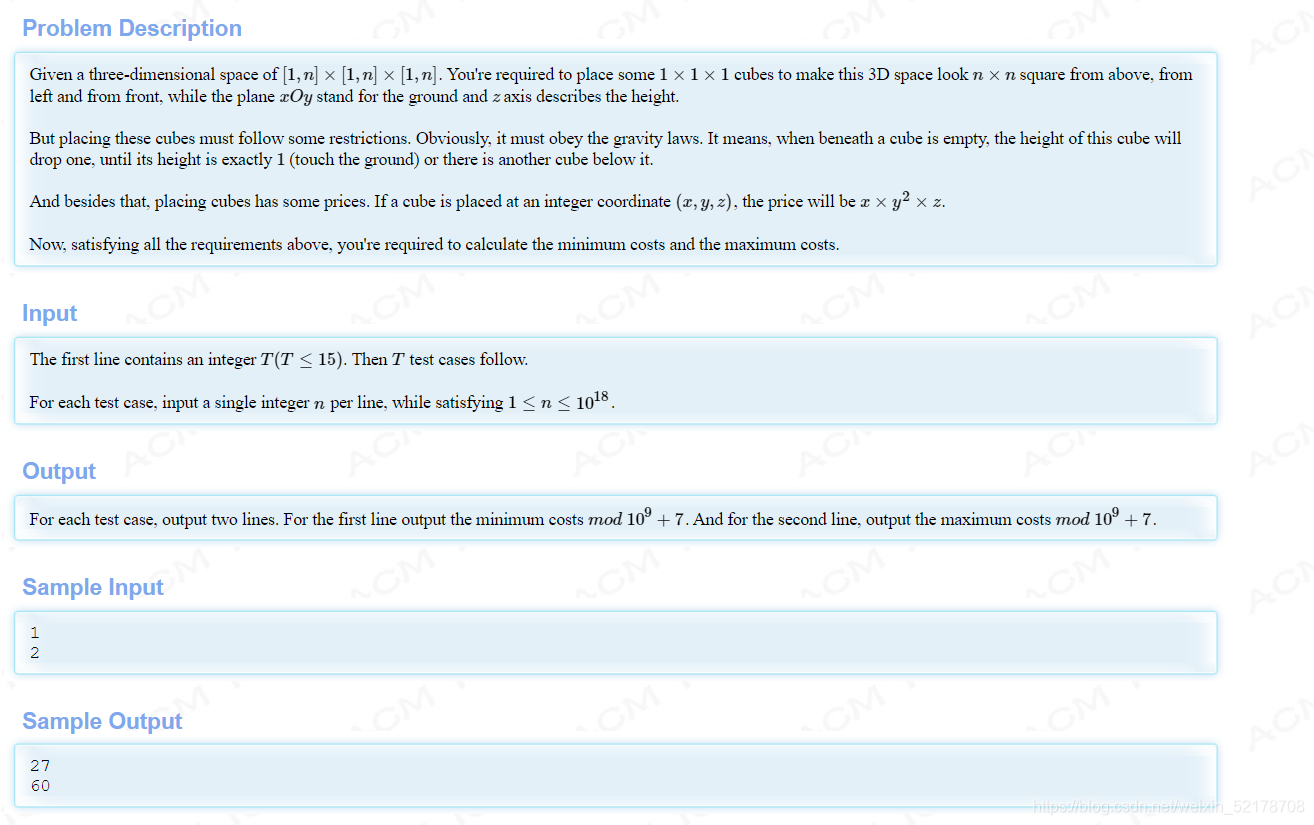
题意
题目的意思是给一个nnn的立方体要我们在这个立方体中放上砖块，使它的正视图，左视图，俯视图都是一个nn的矩阵，并且在规定每一个砖块的贡献是所在位置的（xy²z）的情况下，需要注意的是，每一个砖块所计算的贡献是在最开始放的位置，不是它最后因为重力落下稳定的位置
题解
题目中最有意思的一点就是在计算贡献的时候，计算的是子开始放的位置，所以我们在计算最大值的时候就应该将砖块全部放在最高处
这样的话就都是算的最高处的贡献。
那么有困难的就是最小值怎么计算呢，由于题目规定的要求俯视图也是一个nn的正方形，为了最小，我们就应该将最下面一层全部铺上
那么铺满第一层的花费就应该是**（1+2+3+…+n)(1²+2²+3²+…+n²)1;*
那么对于不是第一层的我们应该怎样计算呢？
首先我们想到的能使正视图和左视图都是nn的正方形的方法就应该是将一整条对角线上的铺满，但是如果是正对角线的话，x和y接近，由初中知识可以知道，当x接近y时，得到的答案一定比x于y相差大的时候大，比如在第n行第n列上，正对角线的贡献应该是n³,而负对角线上的应该是**1*n²**所以我们可以发现，比主对角线更优的是副对角线，那么有没有更优的呢，这个时候，我们可以发现，所有的对角线上的那一个点也可以由最边上的那两个代替

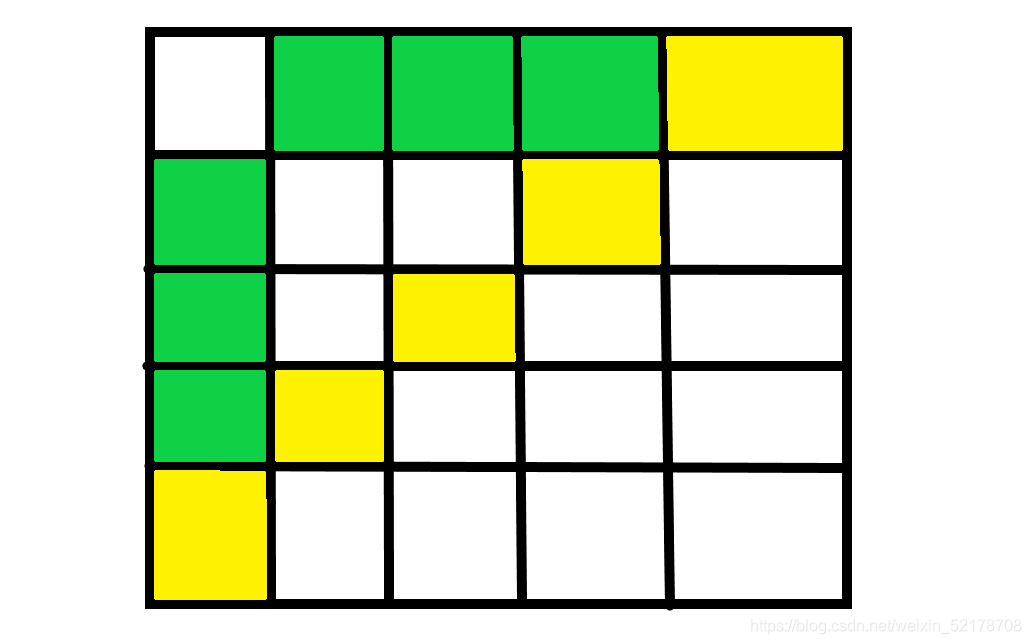
由图我们可以发现，所有黄色的部分我们都可以用绿色的部分来代替，那么怎么证明这样是最优的呢
首先我们不用考虑最边上的两个部分，其次对于剩下的来说应该是
（2(n-1)²）+…+(2²(n-1));
而绿色部分应该是
2²+3²+…(n-1)²+2+3+…(n-1)
两者相减应该是
(n-1)²+2(n-2)²+…+(n-2)2²-(n-1)-(n-2)-…-2
当n>2时都是大于零的
所以绿色的填色方法应该是最优

//#define _ 0
//return ~~(0^_^0)~~
#include<vector>
#include<string>
#include<iostream>
#include<iomanip>
#include<algorithm>
#include<cmath>
#include<map>
using namespace std;
#define int long long
const int mod = 1e9 + 7;
int qmi(int a, int b) {
        int res = 1;
        while (b) {
            if (b & 1)res = (res * a) % mod;
            b >>= 1;
            a = (a * a) % mod;
        }
        return res;
    }
void solve() {
        int n; cin >> n;
        n = n % mod;
        int n1 = (n * (n + 1) % mod * ((2 * n % mod + 1) % mod)) % mod * qmi(6, mod - 2) % mod;
        int n2 = n * (n + 1) % mod * qmi(2, mod - 2) % mod;
        int n3 = n * n % mod;
        int ma = n1 * n2 % mod * n3 % mod;
        int n4 = (n - 1 + mod) % mod * (2 + n) % mod * qmi(2, mod - 2) % mod;
        int n5 = (n * (n + 1) % mod * ((2 * n % mod + 1) % mod) % mod * qmi(6, mod - 2) % mod - 1 + mod) % mod;
        int n6 = (n - 1 + mod) % mod * (2 + n) % mod * qmi(2, mod - 2) % mod;
        int n7 = n1 * n2 % mod;
        int mi = n7 + (n4 + n5) % mod * n6 % mod;
        cout << mi % mod << endl << ma % mod << endl;
}
signed main() {
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	int T;
	cin >> T;
	while (T--)solve();
}