牛客暑期多校第一场

最新推荐文章于 2024-08-01 20:36:34 发布

原创最新推荐文章于 2024-08-01 20:36:34 发布 · 119 阅读

0 ·

CC 4.0 BY-SA版权

牛客专栏收录该内容

6 篇文章

订阅专栏

这篇博客探讨了几何问题在编程竞赛中的应用，包括球体与梯形的碰撞判断，以及如何计算球体被卡住的高度。此外，还讨论了如何在字符矩阵中寻找特定长度的连续零字符串，以及在100-200之间的3友好数的规律。文章还涉及了博弈论，分析了Alice和Bob在取石子游戏中的最优策略，以及在数组元素交换中最大化绝对差值的方法。

牛客多校第一场（罚坐）

B-Ball Dropping

A standard sphere ball is falling in the air, and the center of the sphere is exactly on the centerline of an empty isosceles trapezoidal. The trapezoid is hanging horizontally under the sphere.
Please determine whether the ball will get stuck in the trapezoid or drop past the trapezoid.
输入

The input contains four integers r, a, b, h(1 \le r,a,b,h \le 1000, a

b)r,a,b,h(1≤r,a,b,h≤1000,a>b), indicating the radius of the ball, the top base, the bottom base, and the height of the isosceles
trapezoid.

It is guaranteed that 2r != b , 2r < a , 2r < h.

输出

Output ‘Drop’ if the sphere ball will drop past the empty trapezoid,
otherwise output ‘Stuck’. If the answer is ‘Stuck’, please also
calculate the stuck position(the height between the center of the
sphere and the midpoint of the bottom base). Your answer is considered
correct if its absolute or relative error does not exceed 0.000001

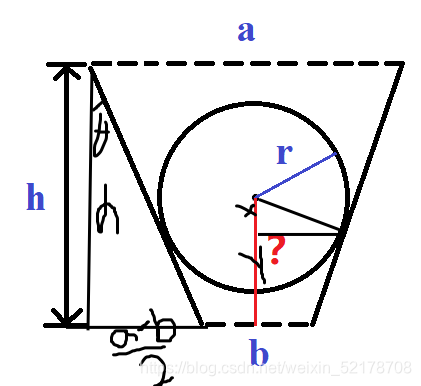
在这里插入图片描述
由图中可知
可以将所求边换成x+y， x=r * sinc，y=h*(2rcosc-b)/(a-b);
其中，sinc=h/sqrt(hh+(a+b)(a+b)/4);
cosc=((a+b)/2)/sqrt(hh+(a+b)(a+b)/4);
由此就可以计算出来x+y的值即为我们所求的值
最后按精度输出即可

    #include<iostream>
#include<algorithm>
#include<iomanip>
using namespace std;
int main(){
    double r,a,b,h;
    cin>>r>>a>>b>>h;
    if(2*r<=b){
        cout<<"Drop"<<endl;
    }
    else {
        cout<<"Stuck"<<endl;
        double c=(a-b)/2;
    double si=c/sqrt(c*c+h*h);
    double cs=h/sqrt(c*c+h*h);
    double sum=r*si+h*(2*r*cs-b)/(a-b);
    cout<<fixed<<setprecision(10)<<sum<<endl;
    }
    
}

Determine the Photo Position

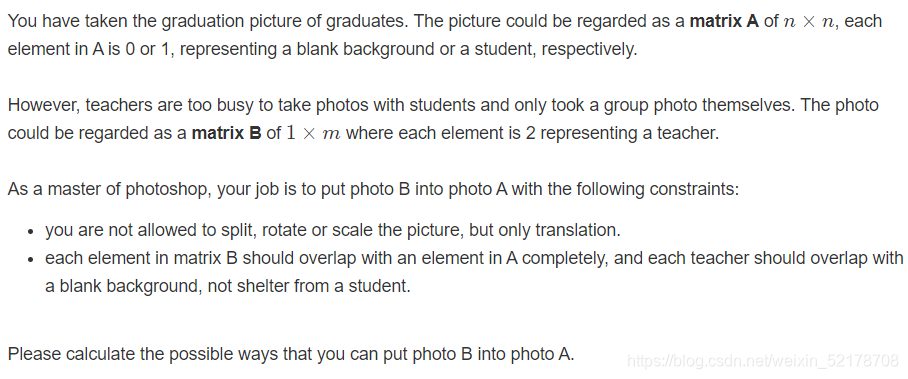
在这里插入图片描述

题目的意思是给一个n*n的字符矩阵，将长度为m的老师覆盖在为字符矩阵中为零的地方，并且要求老师不能覆盖同学
我们只需要找到有多少个长度为m的连续为零的字符串（只能横着放）逐个加起来输出最后的结果。

#include<iostream>
#include<vector>
#include<string>
using namespace std;
int main() {
    int n, l;
    cin >> n >> l;
    vector<string>s(n);
    for (int i = 0; i < n; i++)cin >> s[i];
    string str;
    cin >> str;
    long long sum = 0;
    for (int i = 0; i < n; i++) {
        int flag = 0;
        for (int j = 0; j < n; j++) {
            if (s[i][j] == '0') {
                flag++;
            }
            else {
                flag = 0;
            }
             if(flag>=l)sum++;
        }
    }
    cout << sum << endl;
}

Find 3-friendly Integers

在这里插入图片描述
做着道题的时候感觉自己和傻子一样，将100-200中的所有数都列了出来发现全部都是3友好数
具体思考是以为在逐渐递增的时候满足条件的数会越来越涵盖整个区间，而且只会增不会减，
所以想这道题的时候就在思考多少以后是全部满足条件的，最后发现在100以后是全部满足的而且
前一百个数中只有76个是满足的那么对于大于100的数就非常好计算了至于要用x-24就可以求出
在一百以内的数可以通过离线算或者是直接暴力的方法得到，给我们一个区间求区间内部的所有值
实际上我们可以转换为1到又端点中满足的数的个数减去1到左端点 - 1满足的个数。
原题链接
https://ac.nowcoder.com/acm/contest/11166/F

#include<iostream>
#include<vector>
using namespace std;
long long ste(long long x){
    if(x>=100)return x-24;
    long long sum=0;
    for(int i=1; i<=x; i++) {
            if(i%3==0)  sum++;
            else if(i/10!=0&&((i%10)%3==0||(i/10)%3==0||((i%10)+(i/10))%3==0)) sum++;
        }
    return sum;
}
int main(){
    int t;
    cin>>t;
    
    while(t--){
        long long l,r;
        cin>>l>>r;
        cout<<ste(r)-ste(l-1)<<endl;
    }
}

Alice and Bob

请添加图片描述
题意：
Alice和Bob进行一个游戏，在两堆石头分别为n，m中，在一堆中选取k个石子，在另一堆中选取sk个石子，不能进行这个操作的人输；
因为他们足够聪明，所以他们会尽量找到自己的必胜态，即目标点能不能一步到达。于是我们遍历所有的点，能一步到达0，0或者不能一步到达！（k，ks）就是Alice胜，否则是Bob胜；
原题链接
https://ac.nowcoder.com/acm/contest/11166/A

#include<vector>
#include<iostream>
using namespace std;
bool a[5010][5010];
 
void check(){
    for(int i=0; i<=5000; i++){
        for(int j=0; j<=5000; j++){
            if(a[i][j]==0){
                for(int k=1; k+i<=5000; k++){
                    for(int s=0; s*k+j<=5000; s++){
                        a[k+i][s*k+j] = true;
                    }
                }
                for(int k=1; k+j<=5000; k++){
                    for(int s=0; s*k+i<=5000; s++){
                        a[s*k+i][k+j] = true;
                    }
                }
            }
        }
    }
}
int main() {
    int t;
	check();
    cin >> t;
    while (t--) {
        int m, n;
        cin >> m >> n;
        if (a[m][n])cout << "Alice" << endl;
        else cout << "Bob" << endl;
    }
}

Game of Swapping Numbers

请添加图片描述

题意
本题实际上将是将两个数组对应的位置，其中较大的数赋为正号，较小的数赋为负号，交换A数组中的元素<=k次，得到绝对值相差最大的那一组交换，我们可以先计算出目前的绝对值之和，通过交换使其增加，其实本质上，是我们“减多了“，现在我们将赋正的元素放进一组，将赋负的元素放入一组，我们多减的，实际上就”小数组中最大的元素比大数组中最小的数字”的差，我们要获得最大的差的话，就是要加上这部分减多了的元素。
原题链接
https://ac.nowcoder.com/acm/contest/11166/G

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
	int n, k;
	cin >> n >> k;
	vector<int>a(n);
	vector<int>b(n);
	for (int i = 0; i < n; i++)cin >> a[i];
	for (int i = 0; i < n; i++)cin >> b[i];
	if (n == 2) {
		if (k % 2)swap(a[1], a[0]);
		cout << abs(a[0] - b[0]) + abs(a[1] - b[1]);
		return 0;
	}
	vector<int>ma(n);
	vector<int>mi(n);
	long long sum = 0;
	for (int i = 0; i < n; i++) {
		sum += abs(a[i] - b[i]);
		ma[i] = max(a[i], b[i]);
		mi[i] = min(a[i], b[i]);
	}
	sort(ma.begin(), ma.end());
	sort(mi.begin(), mi.end());
	for (int i = 0; i < min(n, k); i++) {
		if(mi[n-i-1]>ma[i])sum += 2*(mi[n-1-i]-ma[i]);
	}
	cout << sum << endl;
}