了解优先级队列（堆）

堆

堆的定义

把所有元素按照完全二叉树的顺序存储方式存储。
堆，堆在逻辑上是一个完全二叉树，实质上是一个顺序表。

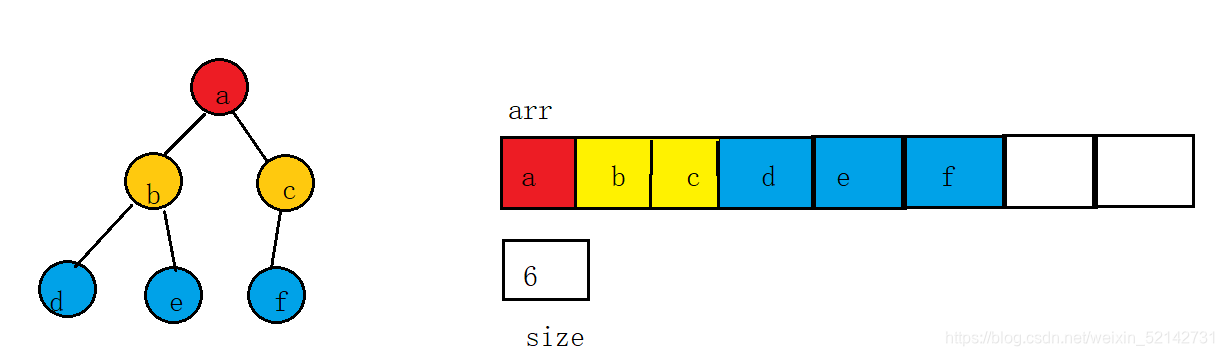
将元素放入数组中，可以根据二叉树的性质将其还原：
假设数组下标为i,
如果i为0，代表根节点
其双亲节点为 (i -1 ) / 2

大小堆

将根节点最大的堆叫大堆，根节点最小的堆叫小堆

• 堆中的某个结点值，总是不大于或者不小于其父节点的值
• 堆总是一颗完全二叉树

根据有序数组，我们可以推出它是堆，但是根据堆不可以推出它有序。

堆的创建

向下调整

前提：是完全二叉树，并且只有一个位置破坏了堆的性质，其余位置满足太条件。
例如：
上图中，只有27不满足，我们需要将更节点向下调整。

思路：index表示需要调整的位置，

1. 判断index是否为叶子结点，如果是本次调整结束
2. 取index中两个孩子最小元素
3. 如果比最小元素小，调整结束，否则交换位置
4. 将index置位最小元素下标，在此判断是否需要向下调整。

代码实现：

    public static void heapify(int[] array, int size, int index) {
        while (true) {
            int leftIndex = 2 * index + 1;
            if (leftIndex >= size) {
                return;
            }
            int minIndex = leftIndex;
            int rightIndex = leftIndex + 1;
            if (rightIndex < size && array[rightIndex] < array[leftIndex]) {
                minIndex = rightIndex;
            }
            if (array[minIndex] >= array[index]) {
                return;
            }
            int t = array[index];
            array[index] = array[minIndex];
            array[minIndex] = t;

            index = minIndex;
        }
    }

建堆

给定一个数字，给定有效数据个数，我们将其变成一个堆。
思路：
我们找到倒数第一个非叶子节点，然后从其位置向头结点一直向下调整，如图：

代码实现：

    public static void createHeap(int[] array, int size) {
        //最后一个结点为size-1，，最后一个非叶子结点为（size-1-1）/2
        int last = (size - 2) / 2;
        for (int i = last; i >= 0; i--) {
            //向下取整
            heapify(array, size, i);
        }
    }

优先级队列

Java 中给我们提供了PriorityQueue的优先级队列（小堆），

函数名	功能
Boolean add()	插入
E remove()	删除
E element	查看堆顶元素

PriorityQueue是小堆，但是我们想让他返回其最大的元素，那么我们需要自己定义比较器：

import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;

public class PriorityQueueDemo {
    static class IntegerComparator implements Comparator<Integer> {
        //返回较大的
        @Override
        public int compare(Integer o1, Integer o2) {
            return -o1.compareTo(o2);
        }
    }

    public static void main(String[] args) {
        Comparator<Integer> comparator = new IntegerComparator();
        System.out.println(comparator.compare(8, 2));   // < 0
        
        Queue<Integer> queue = new PriorityQueue<>(comparator);

        queue.add(9);
        queue.add(5);
        queue.add(2);
        queue.add(7);

        System.out.println(queue.element());
    }
}

模拟实现优先级队列

插入： 尾插，然后向上调整。
删除：头尾交换，向下调整。
查看：直接看第一个元素。

public class MyPriorityQueue {
    //不考虑扩容
    private String[] array = new String[1000];
    private int size = 0;

    public void add(String e) {
        //尾插，然后向上调整
        array[size++] = e;
        shiftUP(size - 1);

    }

    private void shiftUP(int index) {
        while (true) {
            if (index == 0) {
                return;
            }
            int parentIndex = (index - 1) / 2;
            int cmp = array[parentIndex].compareTo(array[index]);
            if (cmp <= 0) {
                return;
            }
            String t = array[index];
            array[index] = array[parentIndex];
            array[parentIndex] = t;

            index = parentIndex;
        }
    }

    public String remove() {
        //将首元素拿出来，并将最后一个元素放在队首，然后向下调整。
        String s = array[0];
        array[0] = array[size - 1];
        size--;
        shiftDown(0);
        return s;
    }

    private void shiftDown(int index) {
        int cmp;
        while (2 * index + 1 < size) {
            int minIndex = 2 * index + 1;
            if (minIndex + 1 < size) {
                cmp = array[minIndex + 1].compareTo(array[minIndex]);
                if (cmp < 0) {
                    minIndex++;
                }
            }
            cmp = array[index].compareTo(array[minIndex]);
            if (cmp <= 0) {
                return;
            }
            String t = array[index];
            array[index] = array[minIndex];
            array[minIndex] = t;
            index = minIndex;

        }
    }

    public String element() {
        return array[0];
    }
}

TOPK问题

关于topK问题，我们需要记住
找前k个最大的，建k个大小的小堆
找前k个最小的，建k个大小的大堆