初识二叉树

树形结构

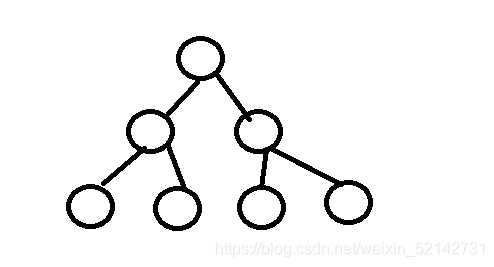
树是一种非线性的数据结构，它由n(n>=0)个有限结点组成。树形结构像一颗倒挂的树。

概念

1、结点：树由结点组成，根节点没有前驱结点，除了根节点，其余每个结点有且仅有一个前驱，可以有0个或多个后继。
N个结点有n-1条边。
2、结点的度：一个节点含有的子树的个数称为结点的度；
3、树的度：一棵树中，最大结点的度称为树的度。
4、叶子结点：度为0的结点称为叶节点。（没有后继的结点）
4、树的深度：树中，结点最大层次；如上图：树高度为4

二叉树

二叉树：
每个结点最多有两棵子树，且二叉树中不存在度大于2的结点。
二叉树是有序树 子树有左右之分。

二叉树的基本形态

空树、只有根节点的二叉树、只有左子树、只有有子树、左右子树都存在

两种二叉树

满二叉树

满二叉树结点总数是 2^K-1(k为层数)
第n层的结点数为 2^n-1
如果一个二叉树，每层结点树都达到最大值，则这个数为满二叉树；
如图：

完全二叉树

完全二叉树是由满二叉树而引出的。对于深度为k的，有n个结点的二叉树，当且仅当其没一个节点都与深度为k的满二叉树中编号从1至n的结点对应则是完全二叉树。
满二叉树是一种特殊的完全二叉树
如图：

二叉树的性质

1、根节点的层数为1，那么一个非空二叉树第i层，最多有2^i-1 个结点
2、根节点的二叉树深度为1，那么深度为k的二叉树最大节点数为2^k-1
3、如果叶节点的个数为n0，度为2的非叶节点的个数为n2，则 n0 = n2 + 1；
4、对于n个结点的完全二叉树，深度 k = log ₂（n+1）向上取整

假设一颗完全二叉树，共2000个结点，则该二叉树中有多少个叶子结点，多少非叶子节点，多少结点只有左孩子， 多少结点只有右孩子。

二叉树的遍历

二叉树的遍历主要分为深度优先和广度优先。
深度优先的遍历分为：前序遍历、中序遍历、后序遍历

前序遍历

又称为先序遍历，访问顺序为——访问根节点->根的左子树->根的右子树

中序遍历

访问顺序为——根的左子树->访问根节点->根的右子树

后序遍历

访问顺序为——根的左子树->根的右子树->访问根节点

对于前中后序遍历，我们可以理解为对根节点的处理顺序，根节点在前处理就是前序遍历…

我们还可以这样理解：
当遍历这课二叉树，我们会经过一个结点3次，当第一次经过就处理就是前序遍历，第二次经过就是中序遍历，第三次就是后序遍历。

前中后序遍历的练习：