LeetCode每日一题（10）——三维形体投影面积（保姆级）

1.题目

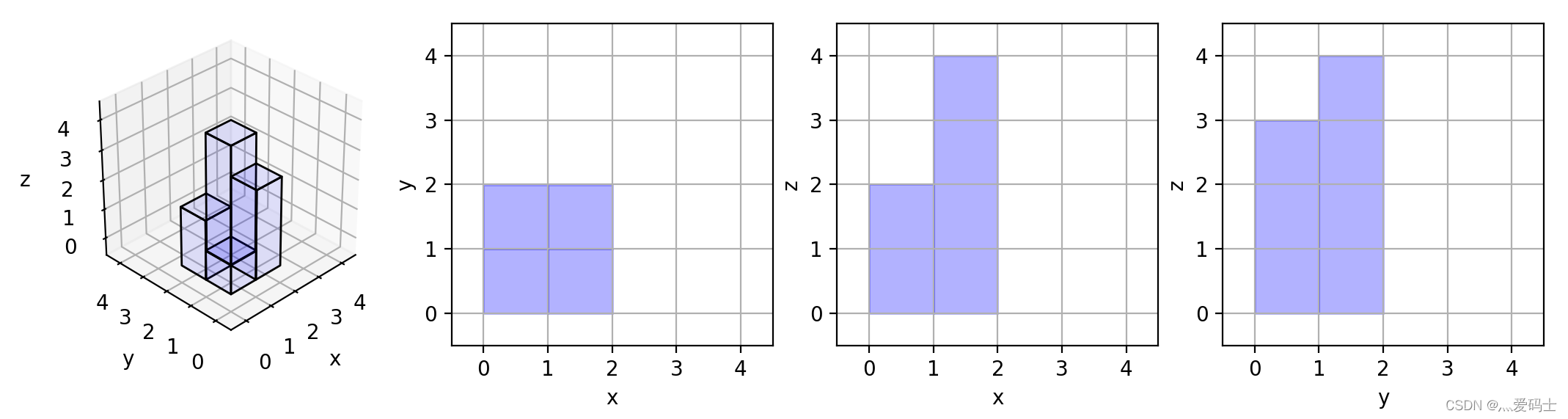
在 n x n 的网格 grid 中，我们放置了一些与 x，y，z 三轴对齐的 1 x 1 x 1 立方体。

每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。

现在，我们查看这些立方体在 xy 、yz 和 zx 平面上的投影。

投影 就像影子，将 三维 形体映射到一个 二维 平面上。从顶部、前面和侧面看立方体时，我们会看到“影子”。

返回 所有三个投影的总面积 。

2.示例

示例 1：

输入：[[1,2],[3,4]]
输出：17
解释：这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 2:

输入：grid = [[2]] 输出：5

示例 3：

输入：[[1,0],[0,2]] 输出：8

提示：

n == grid.length == grid[i].length
1 <= n <= 50
0 <= grid[i][j] <= 50

3.思路

理解题目

首先要理解题目所描述的内容是什么，结合示例我做下简单的解释，自己已经理解题目说的什么意思可以直接去看代码。
题目说给你一个立体图形，让你求他的正视图，左视图，俯视图面积的和。
关于这个立体图形的组成，由一些边长是1的小正方体堆成，放在一个方形区域内。
正方形区域是由一个二维数组组成的，这个二维数组的行数和列数一样，二维数组有几个数字，就有几个位置可以放小正方形，所以小正方形放的范围一定在一个大正方形的范围里。当然小正方形上面可以摞上更多的小正方形。
每一个数组中的数字的位置上放的小正方形的数量=这个数字
示例1的图很清楚，
示例2的意思是在一个1*1的数组上放2个小正方形，正视图2+左视图2+俯视图1=5
示例三的意思是在（0，0）放1个，在（2，2）放两个，正视图3+左视图3+俯视图2=8

解题思路

对于正视图和左视图，算面积都该用每一列的最大高度去算。
用双重for循环遍历数组，统计出左视图和正视图的每一列最高是多少，每一列的面积相加，最后加上俯视图面积即可。
俯视图最简单，数组的哪个位置放了方块，不管几个都只能看到一个，所以有几个数字不为0，俯视图的面积就是几。
求左视图的和正视图的请自行结合代码理解

4.代码

func projectionArea(grid [][]int) int {

	//总面积
	var area int
	//左视图一列的最大高度
	var maxLeft int
	//正视图每一列的最大高度
	var maxFront []int

	//遍历二维数组
	for k1, v1 := range grid{
		for k2, v2 := range v1{
			if grid[k1][k2] > maxLeft {
				maxLeft = v2
			}

			//找到正视图每一列的最大高度
			if k1 == 0 {
				maxFront = append(maxFront, v2)
			}
			if grid[k1][k2] > maxFront[k2] {
				maxFront[k2] = grid[k1][k2]
			}

			//加上俯视图面积
			if v2 != 0 {
				area = area + 1 * 1
				log.Println("附视图面积+1")
			}
		}

		//加上左视图面积
		area = area + maxLeft * 1
		log.Printf("左视图面积+%v", maxLeft)
		maxLeft = 0
	}

	//加上正视图面积
	for _, h := range maxFront {
		area = area + h * 1
		log.Printf("正视图面积+%v", h)
	}
	return area
}