求解单源最短路径问题

LackWood

已于 2023-03-08 17:25:01 修改

阅读量454

点赞数

分类专栏：数据结构文章标签：算法宽度优先图论

于 2023-03-07 20:24:02 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_51780040/article/details/129388931

版权

数据结构专栏收录该内容

4 篇文章

订阅专栏

求解单源最短路径问题

一、图的广度优先遍历BFS

概念

图的广度优先遍历类似于树的层序遍历，基本的思想是首先访问起始顶点 $v_0$ ，接着访问 $v_0$ 未被访问过的邻接顶点 $v_1$ 、 $v_2$ 、…、 $v_i$ ，之后对 $v_1$ 、 $v_2$ 、…、 $v_i$ 重复对 $v_0$ 的操作，直至遍历完图中的所有顶点。
当然，如果这个图是非连通的，那么从 $v_0$ 出发，就只能访问 $v_0$ 所在的连通分量中的全部顶点，至于图中其余未被访问的顶点，只能从中重新选择一个起始顶点，重复之前的操作，直至所有的顶点都被访问。
需要注意的是，在访问的过程中，我们需要一个辅助队列，每访问一个顶点，我们都需要将对应顶点的未被访问过的邻接顶点入队。
而且和树的层序遍历不同的是，图中的每一个顶点可能和图中其他任意顶点邻接，所以在遍历的过程中，我们就要防止已经访问过的顶点，再次以其他顶点的邻接顶点的身份被访问。我们需要增加一个布尔类型的数组来达到这个目的，每个顶点对应数组中的一个元素，值为true，表示已经被访问过，否则就是未被访问。

例子
如图：

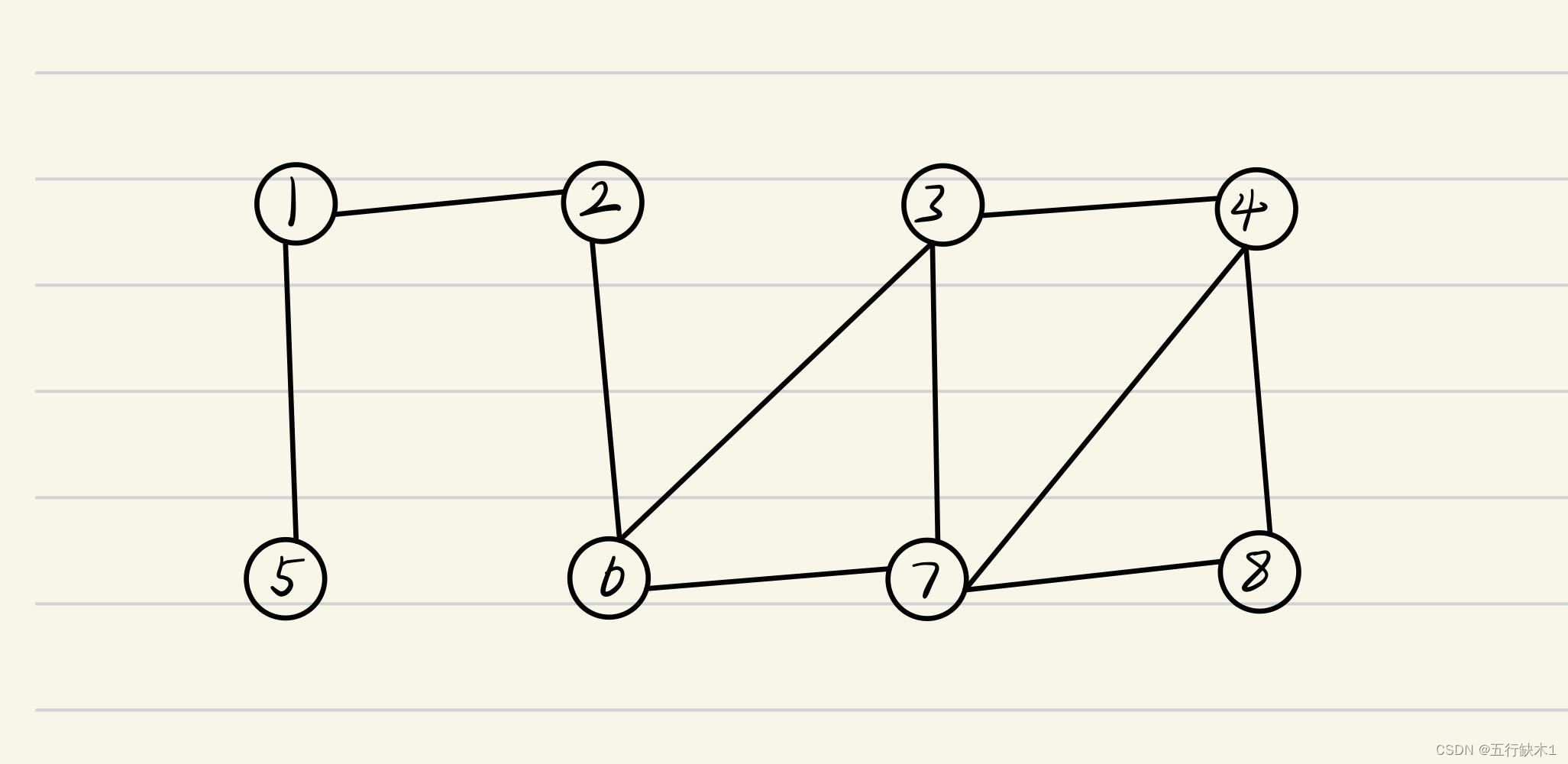
假设起始顶点是 $v_1$ ，我们先访问 $v_1$ ，之后访问 $v_1$ 的邻接顶点 $v_2$ 、 $v_5$ ，然后访问 $v_2$ 的邻接顶点 $v_6$ ，再然后访问 $v_6$ 的邻接顶点 $v_3$ 、 $v_7$ ，接着是 $v_3$ 的邻接顶点 $v_4$ ，以及 $v_7$ 的邻接顶点 $v_8$ 。
最终的遍历序列就是 $v_1$ $v_2$ $v_5$ $v_6$ $v_3$ $v_7$ $v_4$ $v_8$ 。
代码

#include<iostream>
using namespace std;

#define MaxVertexNum 10                      //顶点的数目为8
//定义图
struct MGraph {
	char Vex[MaxVertexNum];                 //顶点表
	int Edge[MaxVertexNum][MaxVertexNum];   //邻接矩阵
	int vexnum, arcnum;                     //当前定点数和弧数
};

//访问标记数组
bool visited[MaxVertexNum];

#pragma region  图的初始化操作

//常用图
void InitMGraph2(MGraph& G)
{
	G.arcnum = 10;
	G.vexnum = 8;
	for (int i = 0; i < 8; i++)
	{
		G.Vex[i] = i + 1 + 48;
	}
	G.Edge[0][4] = G.Edge[4][0] = 1;
	G.Edge[0][1] = G.Edge[1][0] = 1;
	G.Edge[1][5] = G.Edge[5][1] = 1;
	G.Edge[5][2] = G.Edge[2][5] = 1;
	G.Edge[5][6] = G.Edge[6][5] = 1;
	G.Edge[2][6] = G.Edge[6][2] = 1;
	G.Edge[2][3] = G.Edge[3][2] = 1;
	G.Edge[6][3] = G.Edge[3][6] = 1;
	G.Edge[6][7] = G.Edge[7][6] = 1;
	G.Edge[3][7] = G.Edge[7][3] = 1;
}


#pragma endregion

//图的基本操作：寻找某一个节点的第一个邻居结点
int FirstNeighbor(MGraph G, int v)
{
	//遍历第v行
	for (int i = 0; i < G.vexnum; i++)
	{
		//有邻接顶点
		if (G.Edge[v - 1][i] != 0)
		{
			return i + 1;
		}
	}
	//没有邻接顶点
	return -1;
}

//图的基本操作：返回除指定邻居节点的下一个邻接结点
int NextNeighbor(MGraph G, int v, int firstNeighbor)
{
	for (int i = firstNeighbor; i < G.vexnum; i++)
	{
		//找到了下一个邻接结点
		if (G.Edge[v - 1][i] != 0)
			return i + 1;
	}
	//没有下一个邻接结点了
	return -1;
}

//定义全局变量图：
MGraph G;

//访问结点
void visit(int w)
{
	cout << G.Vex[w - 1] << endl;
}


//辅助队列
//定义队列
struct SqQueue {
	int data[MaxVertexNum];   //使用静态数组存储队列
	int front, rear;     //队头指针，队尾指针
};

//初始化队列1，队头指针指向表头元素，队尾指针指向表尾元素的下一位
void InitQueue1(SqQueue& S)
{
	//确定队头指针和队尾指针的指向
	S.front = S.rear = 0;
}

//判断队列是否为空，能这么判断队列为空，是因为对头元素的前一个位置不能存储元素
bool Empty1(SqQueue& S)
{
	//对头指针和队尾指针指向同一个位置
	if (S.front == S.rear)
		return true;
	else
		return false;
}

//判断队列是否已经满了
bool isFull1(SqQueue& S)
{
	//条件是 队尾指针指向对头指针的前一个位置
	if (S.rear + 1 == S.front)
		return true;
	else
		return false;
}

//入队操作
bool EnQueue1(SqQueue& S,int e)
{
	//判断队列是否已经满了
	if (isFull1(S))
		return false;
	//元素写入，指针加1
	S.data[S.rear] = e;
	S.rear++;
	return true;
}

//出队操作
bool OutQueue1(SqQueue& S, int &x)
{
	//判断队列是否已经空了
	if (Empty1(S))
		return false;
	x = S.data[S.front];
	S.front++;
	return true;
}


#pragma region  广度优先遍历

//定义全部变量队列
SqQueue S;

//BFS算法
void BFS(MGraph G, int v)
{
	visit(v);             //访问当前结点
	visited[v] = true;    //标记已经访问过
	EnQueue1(S, v);       //入队
	while (!Empty1(S))
	{
		OutQueue1(S, v);  //顶点v出队
		for (int w = FirstNeighbor(G, v); w > 0; w = NextNeighbor(G, v, w))
		{
			if (!visited[w])
			{
				visit(w);
				visited[w] = true;
				EnQueue1(S, w);
			}
		}
	}
}

void BESTraverse(MGraph G)
{
	//初始化visited数组
	for (int i = 1; i <= G.vexnum; i++)
	{
		visited[i] = false;
	}
	//初始化队列
	InitQueue1(S);
	for (int i = 1; i <= G.vexnum; i++)
	{
		if (!visited[i])
		{
			BFS(G, i);
		}
	}
}


#pragma endregion

void test()
{
	//初始化图
	//InitMGraph1(G);
	InitMGraph2(G);

	//广度优先遍历结果
	cout << "--------------------" << endl;
	BESTraverse(G);
}

int main()
{
	test();

	system("pause");
	return 0;
}

时间复杂度和空间复杂度

	邻接表	解释	邻接矩阵	解释
时间复杂度	O(\|V\| + \|E\|)	采用邻接表存储方式，每个定点均需访问一次，时间复杂度未O(\|V\|)，在搜索任意一个顶点的邻接点时，每条边至少访问一次，时间复杂度未O(\|E\|)，所以总的总的时间复杂度就是O(\|V\| + \|E\|)	O( $V\|^2$ )	采用邻接矩阵存储时，查找每个顶点的邻接点所需的时间都是O(\|V\|)，所以总的时间复杂度就是O( $V\|^2$ )
空间复杂度	O(\|V\|)	需要使用一个辅助队列，每个节点都需要入队一次，最坏的情况下，时间复杂度未O(\|V\|)	O(\|V\|)	同邻接表

二、BFS算法求解非带权图的单源最短路径

概念

所谓的非带权单源最短路径，就是指边不带权值，或者是边的权值都相等的情况下，求其中一个顶点（源点）到其他顶点的最短路径。
我们的思路如下：在广度优先遍历中，我们首先访问起始顶点 $v_0$ ，之后是 $v_0$ 的邻接顶点 $v_2$ 、 $v_5$ ，显然 $v_2$ 、 $v_5$ 到 $v_0$ 的距离是1，即1条边的距离；之后访问顶点 $v_2$ 的未被访问过的邻接顶点 $v_6$ ，也很容易判断， $v_6$ 到 $v_0$ 的距离是2，以此类推，每一个顶点到 $v_0$ 的距离，都是其前面一个顶点（例如 $v_6$ 前面的顶点是 $v_2$ ）到 $v_0$ 的距离再加1。

代码

我们继续采用上面的例子，对BFS算法做一些小的改动。之前在BFS算法中，我们遍历到每一个顶点时，进行的操作是在控制台打印这个顶点，而现在我们要进行的操作是计算这个顶点到起始顶点的距离：d[w] = d[u] + 1;，w和u的关系上面已经说过。

//求解非带权图的单源最短路径问题
int d[MaxVertexNum];      //记录最短路径长度
int path[MaxVertexNum];  //记录路径
void BFS_MIN_Distance(MGraph G, int u)
{
	//初始化最短路径长度
	for (int i = 1; i < G.vexnum; i++)
	{
		d[i] = INFINITY;
		path[i] = -1;
	}

	visited[u] = true;    //标记已经被访问过
	d[u] = 0;             //出发点到本身的路径长度是0
	EnQueue1(S1, u);       //入队
	while (!Empty1(S1))    //BFS算法主要过程
	{
		OutQueue1(S1, u);  //出队
		for (int w = FirstNeighbor(G, u); w > 0; w = NextNeighbor(G, u, w))
		{
			if (!visited[w])
			{
				visited[w] = true;
				d[w] = d[u] + 1;     //w到起始点的路径长度在前驱节点的基础上 + 1
				path[w] = u;         //w的前驱节点是u
				EnQueue1(S1, w);
			}
		}
	}
}

代码中的path数组，是用来记录每一个顶点的前驱顶点，例如：path[w] = u。

三、Dijkstra算法求解单源最短路径问题

在Dijkstra算法中，我们将图中的所有顶点分为两部分，一部分是已经找到到达起始顶点的最短路径，这部分顶点构成一个集合，记作S，另一部分是还没有找到，这部分顶点同样构成一个集合，记作Q。显然，顶点集V = S + Q。

除此之外，我们还需要借助两个辅助数组：
dist[]：这个数组的长度为有|V|，分别对应 $v_0$ ，…, $v_n$ 这n个顶点，数组中的值dist[i]的含义是顶点 $v_i$ 到达起始顶点 $v_0$ 的最短路径的长度。
path[]：这个数组的长度为有|V|，分别对应 $v_0$ ，…, $v_n$ 这n个顶点，数组中值path[i]的含义是顶点 $v_i$ 到达起始顶点 $v_0$ 的最短路径中，顶点 $v_i$ 的前驱节点在顶点表中的数组下。

在求解的过程中，dist[]和path[]是动态更新的，其实我们一开始也并不知道顶点 $v_i$ 到达起始顶点 $v_0$ 的最短路径是那一条，但是我们会通过算法的执行，让这两个数组中存储的信息变成我们想要的结果。
过程如下：

初始化
我们遍历邻接矩阵，查看图中的顶点和起始顶点之间是否存在边，如果存在，我们在dist[]数组对应的位置上存入对应变得权值，path[]数组中对应位置的值即为起始顶点在数组中的下标；如果不存在，dist[]数组对应的位置的值设为无穷，path[]数组中对应位置的值为-1，表示没有到达起始顶点的路径。目前顶点集S中只有起始顶点 $v_0$ ，顶点集Q中包含 $v_1$ 到 $v_n$ 。
算法流程

我们遍历dist[]数组，从中找到除起始顶点 $v_0$ 以外的其他顶点对应的值中，最小的那个值dist[k]，将对应的顶点 $v_k$ 加入到顶点集S中，dist[k]就是顶点 $v_k$ 到达起始顶点的最短路径的长度 $v_0$ 。
之后我们需要做一个比较，我们需要得到集合Q中的顶点到达 $v_k$ 的距离（在邻接矩阵arcs[][]中可以得到），之后再加上dist[k]，即dist[k] + arcs[k][q]（q属于Q）；之后将dist[k] + arcs[k][q]与dist[q]做对比，如果前者大于后者，不做任何操作，反之，将dist[k] + arcs[k][q]赋值给dist[q]，path[q] = k。
重复1~2，我们发现，每重复一次，都可以将Q中的一个顶点划分到S中，所以最终需要执行n - 1次，才能够找到所有的顶点到达起始顶点 $v_0$ 的最短路径。

时间复杂度	解释	空间复杂度	解释
O( $V\|^2$ )	无论是采用邻接表方式存储，还是采用邻接矩阵的方式进行存储，时间复杂度都是 O( $V\|^2$ )。先说邻接矩阵，我们每一次循环只能为一个顶点找到最短路径，所以总共要循环\|V\| - 1次，而再每一次循环中，我们需要对dist[]数组进行遍历，找到最小的值，这个时间花费为O(\|V\|)，我们还要对dist[]的值进行修改，修改的时候需要遍历邻接矩阵中的某一行，这个时间花销也是O(\|V\|)，总体来算，就是(\|V\| - 1) * (\|V\| + \|V\|)，也就是O( $V\|^2$ ) 。而采用邻接表的方式存储，可以减少修改dist[]数组花费的时间，但是再dist[]数组中选择最小分量的时间不变，因此时间复杂度仍然是O( $V\|^2$ )	O(\|V\|)	这里我们只考虑了算法执行过程中需要消费的空间，而并没有考虑到存储图需要花费的空间，执行算法的过程中我们需要使用两个辅助空间dist[]和path[]，空间花销都是O(\|V\|)