哈夫曼树的建立以及哈夫曼编码的编译以及解码

哈夫曼树的建立以及哈夫曼编码的编译以及解码

数据结构作业—哈夫曼树
此程序的目的是从一个text文本中读取字符，然后依据哈夫曼树的原理，将其中的字母进行编码成二进制字符串，然后输入一个二进制字符串可以将其还原为字母的字符串

text文本

 CHENNINGWILLIAM      //全部为大写字母

输入的二进制字符串

0100010110111001

输出样例

/*
----------------------------------------
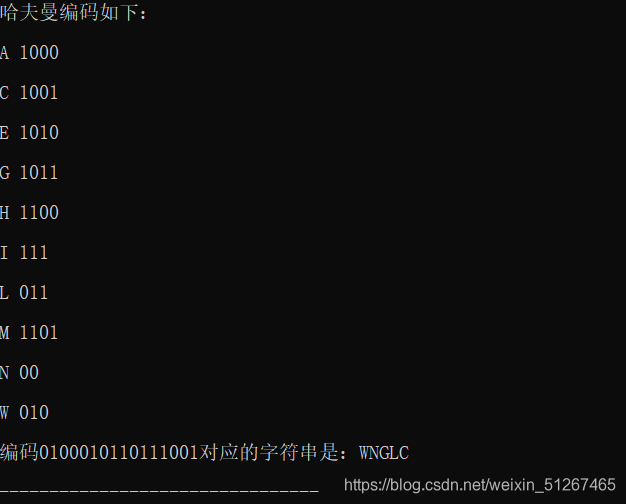
structname : 哈夫曼编码 
author : william
----------------------------------------
*/

#include<iostream>
#include<stdlib.h>
#include<string.h>
#define MAXSIZE 150
#define N 10
using namespace std;

char Str[MAXSIZE];
int statisticsData[128] = {0};
int Index;//下标 
char ch[50];

typedef struct HTNode{ 
  int weight; //结点的权值
  int parent,lchild,rchild; 
}HTNode,*HuffmanTree;

typedef char * HuffmanCode[N+1];

void read_file();
void statistics();
void Select(HuffmanTree HT, int len, int &s1, int &s2);
void CreatHuffmanTree(HuffmanTree &HT,int n);
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode &HC);
void DecodingHuffmanCode(HuffmanTree HT, char *ch, char testDecodingStr[], int len, char *result);

int main()
{
	cout<<"----------------------------------------"<<endl
        <<"structname : 哈夫曼编码"<<endl
        <<"author : william"<<endl
        <<"----------------------------------------"<<endl;
    read_file();
    cout<<"文件中的数据为："<<Str;
    putchar('\n');
    statistics();
	
	HuffmanTree HT;
    CreatHuffmanTree(HT,N);
    cout << "哈夫曼树建立完毕"<<endl<<endl;
    
	HuffmanCode HC;
	CreatHuffmanCode(HT,HC);
  
   //打印哈夫曼编码表
    cout<<"哈夫曼编码如下："<<endl;
	for(int i = 1; i <= N; i++)
	{
	    putchar('\n');
		printf("%c %s\n",ch[i],HC[i]);
	}
	
	char testStr[50] = "0100010110111001";
	int testStrLen = 16;
	putchar('\n');
	printf("编码%s对应的字符串是：", testStr);
	char result[30];//存储解码以后的字符串
	DecodingHuffmanCode(HT, ch, testStr, testStrLen, result);//解码（译码），通过一段给定的编码翻译成对应的字符串
	printf("%s\n", result);
    return 0;
}

void read_file()
{
    FILE *fp;   
    char ch;//用于临时储存 
    
	fp = fopen("test.txt","r");
    while(fscanf(fp,"%c",&ch) != EOF)
    {   	
    	Str[Index] = ch;//将文件中的数据存储到数组中 
    	Index++;
    }
    fclose(fp);
} 

void statistics()
{
	for(int i = 0;i<Index;i++)
	{
		statisticsData[Str[i]] += 1;
	}
	cout<<"如下为统计结果:"<<endl; 	
	for(int i = 65;i<91;i++)
	{
		printf("%c %d;",i,statisticsData[i]);
	}
	putchar('\n');
}

void Select(HuffmanTree HT, int len, int &s1, int &s2)
{
    int i, min1 = 9999, min2 = 9999; //先赋予最大值
    for (i = 1; i <= len; i++)
    {
        if (HT[i].weight < min1 && HT[i].parent == 0)
        {
            min1 = HT[i].weight;
            s1 = i;
        }
    }
    int temp = HT[s1].weight; //将原值存放起来，然后先赋予最大值，防止s1被重复选择
    HT[s1].weight = 9999;
    for (i = 1; i <= len; i++)
    {
        if (HT[i].weight < min2 && HT[i].parent == 0)
        {
            min2 = HT[i].weight;
            s2 = i;
        }
    }
    HT[s1].weight = temp; //恢复原来的值
}

void CreatHuffmanTree(HuffmanTree &HT,int n) 
{//构造哈夫曼树 HT
    int s1,s2;//用于返回最小权值节点的位置坐标 
    if(n <= 1) 
	{
	  return;
    }
    int m = 2*n-1; 
    HT = new HTNode[m+1];  //0 号单元未用，所以需要动态分配 m+1 个单元， HT[m]表示根结点
    for(int i = 1;i <= m;++i)  //将1~m号单元中的双亲、左孩子，右孩子的下标都初始化为0
    {              
        HT[i].parent = 0;
        HT[i].lchild = 0;
        HT[i].rchild = 0;
   } 
   int count = 65;
   
   for(int i = 1;i <= n;++i) //输人前 n 个单元中叶子结点的权值
   {
   	  	while(statisticsData[count] == 0)
   	  	{
          count++;
        }
		HT[i].weight = statisticsData[count];
		ch[i] = count;
		count++;
   }
   /*－ －－－－ －－－－－ －初始化工作结束， 下面开始创建哈夫曼树－ － － － －－－－－－ */ 
   for (int i = n+1; i <= m; ++i) 
   {//通过 n-1 次的选择、删除 、 合并来创建哈夫曼树
    Select(HT,i-1,s1,s2); //在 HT[k]中选择两个其双亲域为0 且权值最小的结点，并返回它们在 HT 中的序号 sl和 s2
    HT[s1].parent = i;
    HT[s2].parent = i; //得到新结点 i, 从森林中删除sl, s2, 将sl和s2 的双亲域由 0改为i.
    HT[i].lchild = s1;
	HT[i].rchild = s2; //s1, s2分别作为i的左右孩子
    HT[i].weight = HT[s1].weight+HT[s2].weight; //权值为左右孩子权值之和
   }
}

//为每个字符求解哈夫曼编码，从叶子到根逆向求解每个字符的哈夫曼编码
void CreatHuffmanCode(HuffmanTree HT, HuffmanCode &HC)
{
	char tmp[N];
	tmp[N-1] = '\0';//编码的结束符
	int start, c, f;
	for(int i = 1; i <= N; i++)
	{//对于第i个待编码字符即第i个带权值的叶子节点
		start = N-1;//编码生成以后，start将指向编码的起始位置
		c = i;
		f = HT[i].parent;
 
		while(f)
		{//f!=0,即f不是根节点的父节点
			if(HT[f].lchild == c)
			{
				tmp[--start] = '0';
			}
			else
			{//HT[f].rchild == c,注意:由于哈夫曼树中只存在叶子节点和度为2的节点，所以除开叶子节点，节点一定有左右2个分支
				tmp[--start] = '1';
			}
			c = f;
			f = HT[f].parent;
		}
		HC[i] = (char *)malloc((N-start)*sizeof(char));//每次tmp的后n-start个位置有编码存在
		strcpy(HC[i], &tmp[start]);//将tmp的后n-start个元素分给H[i]指向的的字符串
	}
}

//解码过程：从哈夫曼树的根节点出发，按字符'0'或'1'确定找其左孩子或右孩子，直至找到叶子节点即可，便求得该字串相应的字符
void DecodingHuffmanCode(HuffmanTree HT, char *ch, char testDecodingStr[], int len, char *result)
{
	int p = 2*N-1;//HT的最后一个节点是根节点，前n个节点是叶子节点
	int i = 0;//指示测试串中的第i个字符
	//char result[30];//存储解码以后的字符串
	int j = 0;//指示结果串中的第j个字符
	while(i<len)
	{
		if(testDecodingStr[i] == '0')
		{
			p = HT[p].lchild;
		}
		if(testDecodingStr[i] == '1')
		{
			p = HT[p].rchild;
		}
 
		if(p <= N)
		{//p<=N则表明p为叶子节点,因为在构造哈夫曼树HT时，HT的m个节点中前n个节点为叶子节点
			result[j] = ch[p];
			j++;
			p = 2*N-1;//p重新指向根节点
		}
		i++;
	}
	result[j] = '\0';//结果串的结束符	
}

作业完毕。