决策树(1)---理论

决策树

基本概念

一种带有判决规则的树，可以根据树中的判决规则来预测未知样本的类别和值。
满足以下几个特征：

1. 叶节点对应决策的结果
2. 内部节点对应一个属性的判断
3. 根节点包含全部训练样本
4. 从根节点到每个叶节点的路径对应一条决策规则

所谓规则简单理解就是的if……then。决策树就是由一些小的分类规则组成的一套规则系统。通过这一套规则系统，我们通过输入要求的属性值，可以给出一个决策结果。

举个栗子:(用于理解随便编的)

一个判断顾客是否会购买商品的决策树：
现在基于三个属性对于顾客是否购买做出决策：年龄、是否学生、信用。构建一颗决策树如下：

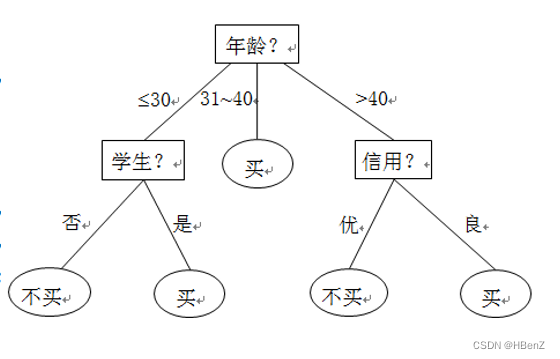
可以看到 这颗树中：
所有的叶节点对应一个决策结果(买/不买)
每一个内部节点都是一个属性判断
每一个根节点到叶节点作为一个规则：对于最左边的决策：首先年龄《=30 --> 是否学生–>是–>不会购买。
同时在树上的内部节点是可能是不符合逻辑的。

那么根据数据来构造出一颗树最重要的是，就是通过算法解决一个问题：
确定属性节点的先后（先进行年龄属性的分类），随后通过属性值下的类别可以进行基类划分

常用算法

首先，可以较好理解的是，一连串的属性中，先进行分类的应该是与决策结果相关性最大的。
比如对于好坏西瓜的判断中我认为”味道“的属性应该是先进行决策的，然后才是有没有籽(因人而异)。
各种算法中改变的就是对于各种属性值对决策结果的”相关性大小“的判别方法。

较为常见的决策树算法有ID3(以信息增益为属性选择)、C4.5(以信息增益率为属性选择)、CART(使用基尼系数作为属性选择)

信息熵(公式推导)

  信息熵用于描述信息的不稳定性，可以理解为信息量的大小。首先，对于一条信息它出现的可能性越小，那么这条信息中的信息量就应该越大。比如： 每天能听到的一些物品的正常价格信息和偶尔听到关于这件物品的打折信息相比，前者所包含的信息量就“小于”后者。因此信息量的大小随着发生概率而递减，且最小为0.
  其次概率与信息量之间的关系应该满足：
  两事件x,y相互独立时

1. 两事件同时发生的信息量的大小等于两事件的信息量大小之和：
   $$E(x,y)=E(x)+E(y)$$

2. 两事件同时发生的概率遵循(因为两事件相互独立)：
   $$p(x,y)=p(x)\ast p(y)$$

3. 任意事件发生概率应该有$p\le 1$,同时对应的信息量有$E\ge 0$

根据1、2可以发现概率的乘积与量的累加相关。就是满足对数关系：
$$\log (p_x)+\log (p_y)=\log (p_x\ast p_y)$$

又因为3所以：
$$E(x)=-\log (p_x)$$

这是单件事情的信息量，那么对于一件信源X={x1,x2,⋯ ,xn}X=\lbrace x_1,x_2,\cdots ,x_n\rbraceX={x1​,x2​,⋯,xn​}的事情来说总信息量就是：
  总信息量=每件事出现的概率*每件事的信息量大小
$$H\left(X\right)=-\sum _{i=1}^{n}p\left(x_i\right)\log (p(x_i))$$

ID3算法

信息增益
上面说到ID3算法使用信息增益作为属性选择依据，明白了信息熵是什么，信息增益也就好懂了。
就是通过指定属性进行分类后的信息量大小与初始的信息量大小的差值。
比如：对于一个信息D(西瓜的好坏)的信息熵为：
$$info(D)=-\sum _{i=1}^{n}p\left(x_i\right){\log }_2(p(x_i))$$
其中X={‘好’,‘坏’}，然后通过给定数据中的概率进行计算(log以2为底是为了方便计算机运算，取多少都行)
对其中的某个属性A(瓜的颜色)来对D进行拟分类分为${}^{\prime }{绿}^{\prime }(D_1)，‘黑绿’(D_2)，‘白’(D_3)$。
那么分类后的信息熵就是所有类别的信息熵之和表示为：
$$inf{o}_A(D)=\sum _{i=1}^{n}info(D_i)$$
那么A属性分类对最终决策的增益量就是：
$$Gain(A)=info(D)-inf{o}_A(D)$$
那么最终算法就是：

//ID3算法伪代码描述
1.计算当前数据中所有属性的信息增益
2.选择信息增益最大属性作为划分，通过该属性值对样本数据进行类别划分
3.如果子样本中只包含决策属性(比如好瓜还是坏瓜)，则为叶子节点，
反之继续递归计算分类。	

优点：理论清晰易懂，方法简单
缺点：一大堆，自己搜吧，这个算法现在使用较少。