C++实现AVL Tree（平衡二叉树）的构建与增删

本文链接：https://blog.youkuaiyun.com/weixin_51049319/article/details/128807651

本文介绍AVLTree平衡二叉树的基本概念及其在插入和删除操作中的平衡调整策略。详细展示了四种不平衡情况（LL、RR、LR、RL）对应的旋转调整方法，并提供了完整的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

C++实现AVL Tree（平衡二叉树）的构建与增删查

AVL Tree 的简介：
AVL Tree平衡的调整：
AVL Tree 的插入
AVL Tree的删除
代码实现
参考与引用

AVL Tree 的简介：

AVL Tree的目的是降低二叉搜索树的成本，避免树的高度增长的过快，因此规定AVL Tree在插入或者删除的时候，任意节点的左右子树的高度差的绝对值小于2。在这里定义平衡因子，它代表着左子树与右子树的高度差，取值为-1，0，1。

AVL Tree平衡的调整：

原因：

在简介中，提到过AVL Tree的任意节点的左右子树的高度差的绝对值小于2，而在插入或删除的时候，这种平衡难免会被打破，这时就要对最小的不平衡的子树做调整，来满足这个大前提。

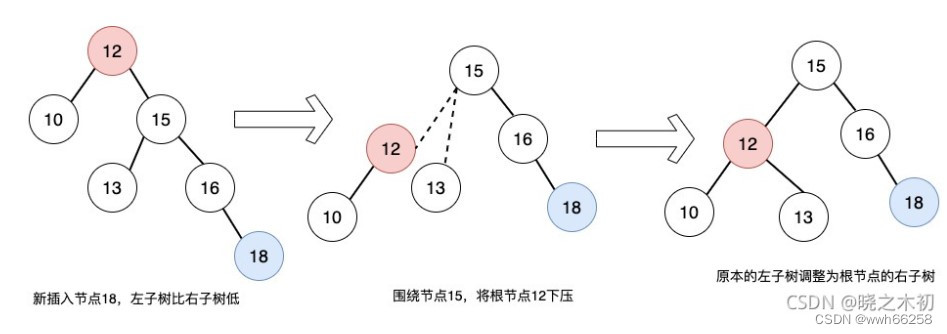
LL——插入的节点在节点的左节点的左节点

此时，左子树高度过大，需要右旋来维持平衡
在这里插入图片描述

TreeNode* AVL::right_rotate(TreeNode* node){
    TreeNode* newnode = node->left;
    node->left = newnode->right;
    newnode->right = node;
    node->height = max(getheight(node->left),getheight(node->right))+1;
    newnode->height = max(getheight(newnode->left),getheight(newnode->right))+1;
    return newnode;
}

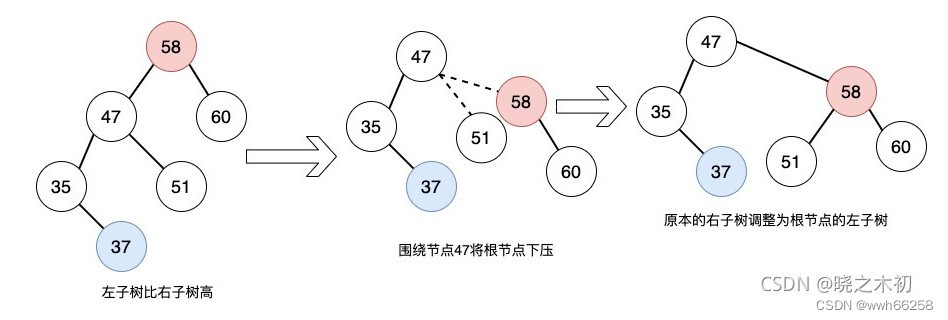
RR——插入的节点在节点的右节点的右节点

此时，左子树的高度过大，需要左旋来平衡
在这里插入图片描述

TreeNode* AVL::left_rotate(TreeNode* node){
    TreeNode* newnode = node->right;
    node->right = newnode->left;
    newnode->left = node;
    node->height = max(getheight(node->left),getheight(node->right))+1;
    newnode->height = max(getheight(newnode->left),getheight(newnode->right))+1;
    return newnode;
}

LR——插入的节点在节点的左节点的右节点

以左儿子为根节点进行左旋，再按原始的根节点右旋
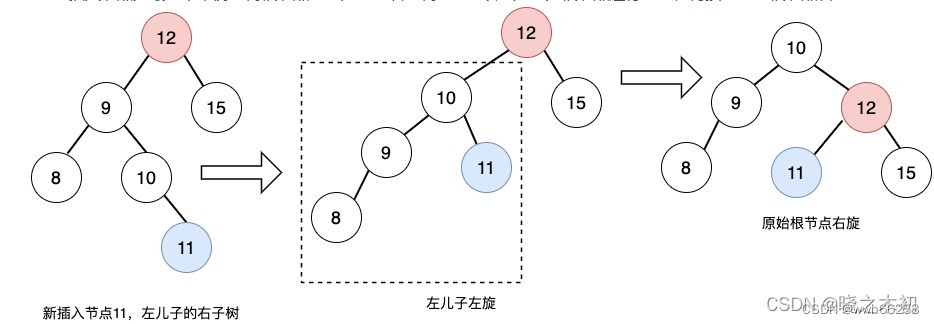
在这里插入图片描述

TreeNode* AVL::left_right_rotate(TreeNode* node){
    node->left = left_rotate(node->left);
    return right_rotate(node);
}

RL——插入的节点在节点的右节点的左节点

以右儿子为根节点进行右旋，再按原始的根节点左旋
在这里插入图片描述

TreeNode* AVL::right_left_rotate(TreeNode* node){
    node->right = right_rotate(node->right);
    return left_rotate(node);
}

AVL Tree 的插入

TreeNode* AVL::node_insert(TreeNode* node, int val){
    if(node == nullptr)return new TreeNode(val,1);
    if(node->val>val){
        node->left = node_insert(node->left,val);
        //左子树插入只会左边不平衡
        if(getheight(node->left)-getheight(node->right)>1){
            if(node->left->val > val){
                node = right_rotate(node);
            }else{
                node = left_right_rotate(node);
            }
        }
    }else if(node->val<val){
        node->right = node_insert(node->right,val);
        //右子树只会右边不平衡
        if(getheight(node->right)-getheight(node->left)>1){
            if(node->right->val>val){
                node = right_left_rotate(node);
            }else{
                node = left_rotate(node);
            }
        }
    }
    node->height = max(getheight(node->left),getheight(node->right))+1;
    return node;
}

AVL Tree的删除

相比于上文 C++实现BST（二叉搜索树）的构建与增删查中给出的删除方法，这里采用了递归的写法，也是参考别人的写法完成的，很受启发。在删除之后引起的不平衡可以理解为等效在另一个子树的增加。通过此方式来完成平衡

TreeNode* AVL::node_delete(TreeNode* node,int val){
    if(!node)return node;
    if(node->val > val){
        node->left = node_delete(node->left,val);
    }else if(node->val < val){
        node->right = node_delete(node->right,val);
    }else{
        if(!node->left&&!node->right){
            node=nullptr;
        }else if(node->right){
            TreeNode* pre = node->right;
            while(pre->left){
                pre=pre->left;
            }
            node->val = pre->val;
            node->right = node_delete(node->right,pre->val);
        }else{
            TreeNode* pre = node->left;
            while(pre->right){
                pre=pre->right;
            }
            node->val = pre->val;
            node->left = node_delete(node->left,pre->val);
        }
    }
    if(!node)return node;
    if(getheight(node->right)-getheight(node->left) > 1){
        //删除发生在左子树，模拟插入发生在右子树
        if(getheight(node->right->right)>getheight(node->right->left)){
            node = right_rotate(node);
        }else{
            node = left_right_rotate(node);
        }
    }
    else if(getheight(node->left)-getheight(node->right) > 1){
        //删除发生在右子树，模拟插入发生在左子树
        if(getheight(node->left->left) > getheight(node->left->right)){
            node = right_left_rotate(node);
        }else{
            node = left_rotate(node);
        }
    }
    node->height = max(getheight(node->left),getheight(node->right))+1;
    return node;
}

代码实现

#include<bits/stdc++.h>
using namespace std;

struct TreeNode {
    int val;
    int height;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x, int y) : val(x), height(y),left(nullptr), right(nullptr){}
    TreeNode(int x, int y, TreeNode *left, TreeNode *right) : val(x), height(y), left(left), right(right){}

};

class AVL{

private:
    TreeNode* root;

    int getheight(TreeNode* node){ return node==nullptr?0:node->height; }

    TreeNode* left_rotate(TreeNode* node);//RR的情况
    TreeNode* right_rotate(TreeNode* node);//LL的情况
    TreeNode* left_right_rotate(TreeNode* node);//LR的情况
    TreeNode* right_left_rotate(TreeNode* node);//RL的情况

    TreeNode* node_insert(TreeNode* node, int val);
    TreeNode* node_delete(TreeNode* node, int val);

    void HierarchicalOrderVisit(TreeNode* node);

public:
    void create(int* nums,int size){
        root=NULL;
        for(int i =0;i<size;i++){
            root = node_insert(root, nums[i]);
        }
    }
    void HierarchicalOrder(){

        HierarchicalOrderVisit(root);
    }
    void Delete(int val){
        root = node_delete(root,val);
    }
};

void AVL::HierarchicalOrderVisit(TreeNode* node){
    queue<TreeNode*> que;
    que.push(node);
    while(!que.empty())
    {
        int size = que.size();
        while(size--){
            TreeNode* nextnode = que.front();
            cout<<nextnode->val<<" ";
            if(nextnode->left)que.push(nextnode->left);
            if(nextnode->right)que.push(nextnode->right);
            que.pop();
        }
        cout<<endl;
    }
}

TreeNode* AVL::left_rotate(TreeNode* node){

    TreeNode* newnode = node->right;
    node->right = newnode->left;
    newnode->left = node;

    node->height = max(getheight(node->left),getheight(node->right))+1;
    newnode->height = max(getheight(newnode->left),getheight(newnode->right))+1;

    return newnode;

}

TreeNode* AVL::right_rotate(TreeNode* node){
    TreeNode* newnode = node->left;
    node->left = newnode->right;
    newnode->right = node;

    node->height = max(getheight(node->left),getheight(node->right))+1;
    newnode->height = max(getheight(newnode->left),getheight(newnode->right))+1;

    return newnode;
}

TreeNode* AVL::left_right_rotate(TreeNode* node){
    node->left = left_rotate(node->left);
    return right_rotate(node);
}

TreeNode* AVL::right_left_rotate(TreeNode* node){
    node->right = right_rotate(node->right);
    return left_rotate(node);
}

TreeNode* AVL::node_insert(TreeNode* node, int val){
    if(node == nullptr)return new TreeNode(val,1);
    if(node->val>val){
        node->left = node_insert(node->left,val);
        //左子树插入只会左边不平衡
        if(getheight(node->left)-getheight(node->right)>1){
            if(node->left->val > val){
                node = right_rotate(node);
            }else{
                node = left_right_rotate(node);
            }
        }
    }else if(node->val<val){
        node->right = node_insert(node->right,val);
        //右子树只会右边不平衡
        if(getheight(node->right)-getheight(node->left)>1){
            if(node->right->val>val){
                node = right_left_rotate(node);
            }else{
                node = left_rotate(node);
            }
        }
    }
    node->height = max(getheight(node->left),getheight(node->right))+1;
    return node;
}

TreeNode* AVL::node_delete(TreeNode* node,int val){
    if(!node)return node;
    if(node->val > val){
        node->left = node_delete(node->left,val);
    }else if(node->val < val){
        node->right = node_delete(node->right,val);
    }else{
        if(!node->left&&!node->right){
            node=nullptr;
        }else if(node->right){
            TreeNode* pre = node->right;
            while(pre->left){
                pre=pre->left;
            }
            node->val = pre->val;
            node->right = node_delete(node->right,pre->val);
        }else{
            TreeNode* pre = node->left;
            while(pre->right){
                pre=pre->right;
            }
            node->val = pre->val;
            node->left = node_delete(node->left,pre->val);
        }
    }

    if(!node)return node;

    if(getheight(node->right)-getheight(node->left) > 1){
        //删除发生在左子树，模拟插入发生在右子树
        if(getheight(node->right->right)>getheight(node->right->left)){
            node = right_rotate(node);
        }else{
            node = left_right_rotate(node);
        }
    }

    else if(getheight(node->left)-getheight(node->right) > 1){
        //删除发生在右子树，模拟插入发生在左子树
        if(getheight(node->left->left) > getheight(node->left->right)){
            node = right_left_rotate(node);
        }else{
            node = left_rotate(node);
        }
    }

    node->height = max(getheight(node->left),getheight(node->right))+1;

    return node;

}

int main(){
    AVL test;
    int nums[8] = {15,23,19,11,25,22,18,16};
    test.create(nums,8);
    test.HierarchicalOrder();
    /*
            19
        15      23
    11     18 22    25
		16

*/
    test.Delete(16);
    test.HierarchicalOrder();
}

参考与引用

平衡二叉树（AVL）