数据结构之堆栈（java编程实现）

数据结构之堆栈（java编程实现）

首先我们了解堆栈的基本概念和特点：
堆栈是一组相同数据类型的组合，所有的操作均在堆栈顶端进行，具有“后进先出”的特性。
所谓后进先出（Last in First out）的概念，其实就如同餐盘由桌面往上一个一个叠放，但是取用时由最上面先拿。堆栈特性如下：
①只能从堆栈的顶端存取数据
②数据的存取符合“First in Last out”原则
堆栈的基本操作有以下五种：
①creat：创建一个空堆栈
②push：把数据压入堆栈顶端，并且得到新堆栈
③pop：从堆栈顶端弹出数据，并且得到新堆栈
④isEmpty：判断堆栈是否为空堆栈，是则返回true，不是则返回false
⑤full：判断堆栈是否已满，是则返回true，不是则返回false
一、用数组实现堆栈
用数组来实现堆栈好处是算法很简单，但是坏处是数组的大小是固定的而堆栈的大小是会变化的，容易造成浪费
算法如下：

//类方法：empty
//判断堆栈是否为空堆栈，如果是返回true，不是则返回false
public boolean empty(){
	if(top==-1)
		return true;
	else
		return false;
}
//类方法：push
//将指定的数据压入堆栈
public boolean push(int data){
	if(top>=stack.length-1){
		System.out.println("堆栈已经满了，无法再压入");
		return false;
	}else{
		stack[++top]=data;
		return true;
	}
}
//类方法：pop
//从堆栈顶端弹出数据
public int pop(){
	if(empty()){//判断堆栈是否为空，如果是则返回-1值
		return -1;
	}else{
		return stack[top--];//先将数据弹出后，再将堆栈指针往下移动
	}
}

基本操作我们都了解了，接下来我们用一个范例来实现用数组描述堆栈：
【范例数组设计堆栈】
请使用数组结构来设计一个堆栈程序，并使用循环来控制准备压入或弹出元素，并仿真堆栈的各种操作，其中必须包括压入（push）与弹出（pop）函数，最后还要输出堆栈内所有元素

package 数组实现堆栈;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

class StackByArray{//以数组模拟堆栈的类声明
	private int[] stack;//在类中声明数组
	private int top;//指向堆栈顶端的索引
	//StackByArray类构造函数
	public StackByArray(int stack_size) {
		stack=new int[stack_size];//建立函数
		top=-1;
	}
	//类方法：push
	//将指定的数据压入堆栈
	public boolean push(int data) {
		if(top>=stack.length-1) {//判断堆栈顶端的指针是否大于数组大小
			System.out.println("堆栈已满，无法再压入");
			return false;
		}else {
			stack[++top]=data;//将数据压入堆栈
			return true;
		}
	}
	//类方法，empty
	//判断堆栈是否为空堆栈，是则返回true，不是则返回false
	public boolean empty() {
		if(top==-1)return true;
		else return false;
	}
	//类方法：pop
	//从堆栈弹出数据
	public int pop() {
		if(empty()) {//判断堆栈是否为空的，如果是则返回-1值
			return -1;
		}else {
			return stack[top--];//先将数据弹出后，再将堆栈指针往下移动
		}
	}
}
//基类的声明
public class 数组堆栈 {
	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader buf;
		int value;
		StackByArray stack=new StackByArray(10);
		buf=new BufferedReader(new InputStreamReader(System.in));
		System.out.println("请按序输入10个数据");
		for(int i=0;i<11;i++) {
			value=Integer.parseInt(buf.readLine());
			stack.push(value);
		}
		System.out.println("===================================");
		while(!stack.empty()) {//将堆栈数据陆续从顶端弹出
			System.out.println("堆栈弹出的顺序为："+stack.pop());
		}
	}
}

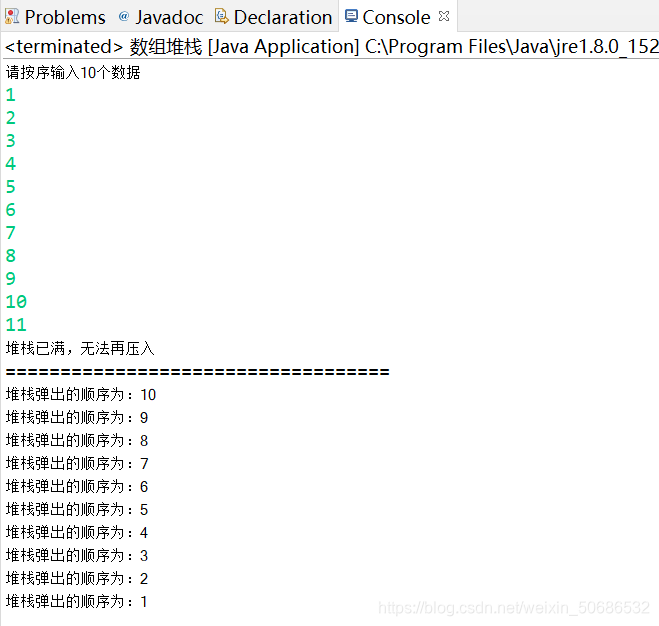
这里我设置了容量为10的堆栈，尝试给它输入11个数据，结果输入最后一个数据时会显示堆栈已经满了。第十一个数据没有存入堆栈。运行结果如下：

【范例数组堆栈二】
用数组仿真扑克排洗牌以及发牌的过程。请用随机数来生成扑克牌后压入堆栈，放满52张牌后开始发牌，使用堆栈的弹出功能来给四个人发牌

package 数组实现堆栈;
//堆栈应用--洗牌与发牌过程
//	0~12梅花
//	13~25方块
//	26~38红桃
//	39~51黑桃
public class 洗扑克牌 {
	static int top=-1;
	public static void main(String[] args) {
		int card[]=new int[52];
		int stack[]=new int[52];
		int i,j,k=0,test;
		char ascVal='0';//初始化
		int style;
		for(i=0;i<52;i++) {
			card[i]=i;
		}
		System.out.println("[洗牌中....请稍后！]");
		while(k<30) {
			for(i=0;i<51;i++) {
				for(j=i+1;j<52;j++) {
					if(((int)(Math.random()*5))==2) {
						test=card[i];//洗牌
						card[i]=card[j];
						card[j]=test;
					}
				}
			}
			k++;
		}
		i=0;
		while(i!=52) {//当i等于52时不再增加,此时top=51
			push(stack,52,card[i]);
			i++;
		}
		System.out.println("[逆时针发牌]");
		System.out.println("[显示各家的牌]\n 东家\t 北家\t 西家\t 南家\t");
		System.out.println("================================================");
		while(top>=0) {
			style=stack[top]/13;
			switch(style){
				case 0://梅花
					ascVal='C';
					break;
				case 1://方块
					ascVal='D';
					break;
				case 2://红桃
					ascVal='H';
					break;
				case 3://黑桃
					ascVal='S';
					break;
			}
			System.out.print("["+ascVal+(stack[top]%13+1)+"]");//输出花色和牌号
			System.out.print("\t");
			if(top%4==0)//每四轮换一行
				System.out.println();
			top--;
		}
	}
	public static void push(int stack[],int MAX,int val) {
		if(top>=MAX-1) {
			System.out.println("[堆栈已经满了]");
		}else {
			top++;
			stack[top]=val;
		}
	}
	//pop函数没有使用
//	public static int pop(int stack[]) {
//		if(top<0){
//			System.out.println("[堆栈已经空了]");
//			return -1;	
//			}
//		return stack[top--];
//	}
}

运行结果如下：

二、用链表实现堆栈
虽然用数组来制作堆栈算法比较简单，但是在制作变动的堆栈的时候数组容易造成大量的浪费。而链表的长度也是随时可以变动的，所以用链表来实现堆栈不会造成空间的浪费。只是算法比较复杂。
链表制作堆栈的相关算法如下：

class Node{//链表节点的声明
	int data;
	Node next;
	public Node(int data){
		this.data=data;
		this.next=null;
	}
}
//类方法：isEmpty
public boolean isEmpty(){
	return front==null;
}
//类方法：insert
public void insert(int data){
	Node newNode=new Node(data);
	if(this.isEmpty){
		front=newNode;
		rear=newNode;
	}else{
		rear.next=newNode;
		rear=newNode;
	}
}
//类方法：pop()
//从堆栈顶端弹出数据
public void pop(){
	Node newNode;
	if(this.isEmpty){
		System.out.println("===当前堆栈为空堆栈===");
		return;
	}else{
		while(newNode.next!=rear)
			newNode=newNode.next;
		newNode.next=rear.next;
		rear=newNode;
	}
}

基本的push和pop算法我们给出了，接下来我们通过一个具体的例题来体验链表制作堆栈的过程。
【范例链表制作堆栈】
请用链表来实现堆栈，并使用循环来控制元素的压入和弹出堆栈，并在最后输出堆栈内的所有元素

package 链表堆栈;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

class Node{
	int data;
	Node next;
	public Node(int data) {
		this.data=data;
		this.next=null;
	}
}
class StackByLink {
	public Node front;//指向链表底部的指针
	public Node rear;//指向链表顶端的指针
	//类方法：isEmpty()
	//判断堆栈如果为空，则front==null
	public boolean isEmpty() {
		return front==null;
	}
	//类方法：output_of_Stack()
	//打印出堆栈中的内容
	public void output_of_Stack() {
		Node current=front;
		while(current!=null) {
			System.out.print("["+current.data+"]");
			current=current.next;
		}
		System.out.println();
	}
	//类方法：insert()
	//把指定的数据压入堆栈
	public void insert(int data) {
		Node newNode=new Node(data);
		if(this.isEmpty()) {//当链表为空，首节点指向末尾节点
			front=newNode;
			rear=newNode;
		}else {
			rear.next=newNode;
			rear=newNode;
		}
	}
	//类方法：pop()
	//从链表顶部弹出指针
	public void pop() {
		Node newNode;
		if(this.isEmpty()) {
			System.out.print("===当前堆栈为空堆栈===\n");
			return;
		}
		newNode=front;
		if(newNode==rear) {
			front=null;
			rear=null;
			System.out.print("===当前堆栈为空堆栈===\n");
		}else {
			while(newNode.next!=rear) {
				newNode=newNode.next;
			}
			newNode.next=rear.next;
			rear=newNode;
		}
	}
}
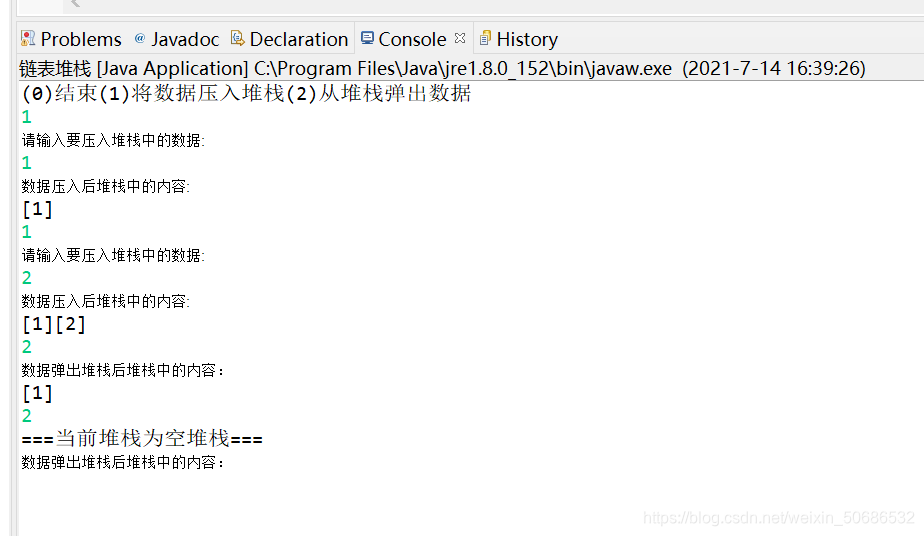
public class 链表堆栈 {
	public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader buf=new BufferedReader(new InputStreamReader(System.in));
		StackByLink stack_by_Linkedlist=new StackByLink();
		int choice=0;
		System.out.println("(0)结束(1)将数据压入堆栈(2)从堆栈弹出数据");
		while(true) {
			choice=Integer.parseInt(buf.readLine());
			if(choice==2) {
				stack_by_Linkedlist.pop();
				System.out.println("数据弹出堆栈后堆栈中的内容：");
				stack_by_Linkedlist.output_of_Stack();
			}else if(choice==1) {
				System.out.println("请输入要压入堆栈中的数据:");
				stack_by_Linkedlist.insert(Integer.parseInt(buf.readLine()));
				System.out.println("数据压入后堆栈中的内容:");
				stack_by_Linkedlist.output_of_Stack();
				
			}else if(choice==0) {
				break;
			}else {
				System.out.println("错误");
			}
		}
	}
}

【汉诺塔问题解法】
汉诺塔问题的描述：假设有A、B、C三个木桩和n个大小均不相同的盒子（Disc），从小到大编号为1，2，3，…,n，编号越大直径越大。开始的时候，n个盘子都套在A木桩上，现在希望能找到可以将A木桩上的盘子借着B木桩当中间桥梁，全部移动到C木桩上次数最少的方法。
规则说明：
（1）直径较小的盘子永远只能置于直径较大的盘子上
（2）盘子可以任意地从任何一个木桩移动到其他木桩上
（3）每一次只能移动一个盘子，而且只能从最上面的盘子开始移动。
编程策略选择：应该可以发现汉诺塔问题非常适合以递归方式与堆栈来解决。因为她满足了递归的两大特性：一是有反复执行的过程；二是有停止的出口。
步骤一：将n-1个盘子，从木桩1移动到木桩2
步骤二：将第n个最大盘子，从木桩1移动到木桩3
步骤三：将第n-1个盘子，从木桩2移动到木桩3
算法如下：

package 汉诺塔问题;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class 汉诺塔问题 {
	static int i=0;
	public static void main(String[] args) throws IOException {
		int j;
		String str;
		BufferedReader keyin=new BufferedReader(new InputStreamReader(System.in));
		System.out.print("请输入盘子的数量:");
		str=keyin.readLine();
		j=Integer.parseInt(str);
		hanoi(j,1,2,3);	
		System.out.println("盘子移动"+i+"次");
	}
	public static void hanoi(int n,int p1,int p2,int p3) {
		i++;
		if(n==1) {
			System.out.println("盘子从"+p1+"移动到"+p3);//
		
		}else {
			hanoi(n-1,p1,p3,p2);
			System.out.println("盘子从"+p1+"移动到"+p3);
			hanoi(n-1,p2,p1,p3);
		}
	}
}

测试运行结果如下：

补充：从数学上，有n个盘子汉诺塔问题就需要移动2的n次方减1次。
【老鼠走迷宫】
堆栈的应用还有一个相当有趣的问题，就是实验心里学中有名的“老鼠走迷宫”问题。老鼠走迷宫问题称述是：假设把一只大老鼠放在一个没有盖子的大米公告盒子的入口处，盒子中有许多墙使得大部分路程都被挡住而无法前进。老鼠可以按照尝试错误的方法找到出口。不过，这只老鼠必须具备走错路就会退回来并把走错的路记下，避免下次走重复的路，就这样知道找到出口为止。简单来说，老鼠行进时，必须符合以下三个原则：
（1）一次只能走一格
（2）遇到墙无法前进走时，则退回一步找找看是否有其他路可走
（3）走过的路不会走第二次
在写走迷宫之前，我们先做一个迷宫的墙。用一个二维数组MAZE[row][col]实现，
MAZE[i][j]=1表示[i][j]处有墙，无法通过
MAZE[i][j]=0表示[i][j]处无墙，可以通过
MAZE[1][1]是入口，MAZE[m][n]是出口

小老鼠可以选择的方向共有四个，分别为东、西、南、北。但并非每个位置都有四个方向可以选择，关键看MAZE的值是否为0.
我们可以使用链表来记录走过的位置，并且将走过的位置对应的数组元素内容标记为2，然后将这个位置从放入堆栈再进行下一次的选择。如果走到死胡同并且还没抵达终点，那么就退出上一个位置，并退回去知道回到上一个岔路后再选择其他的路。由于每次新加入的位置必定回在堆栈的顶端，因此堆栈顶端指针所指的方格编号便是当前搜索迷宫出口的老鼠所在的位置。如此重复这些动作直到走到出口为止。
上面的搜索迷宫过程可以用Java算法描述：

if(上一格可走)
{
	把方格编号压入堆栈;
	往上走;
	判断是否为出口;
}else if(下一个方格可走){
	把方格编号压入堆栈;
	往下走;
	判断是否为出口;
}else if(左一格可走){
	把方格编号压入堆栈;
	往左走;
	判断是否为出口;
}else if(右一格可走){
	把方格编号压入堆栈;
	往右走;
	判断是否为出口;
}else{
	从堆栈中删除一方格编号;
	从堆栈中弹出一方格编号;
	往回走;
}

上面的算法是每次进行移动时所执行的操作，其主要时判断当前所在位置的上下左右是否有可以前进的方格。若找到可前进的方格，便将方格的编号压入到记录移动路径的堆栈中，并往该方格移动，而当四周没有可走的方格时，也就是当前所在的方格无法走出迷宫，则必须他退回到前一格重新再来检查是否有其他可走的路径。所以在上面的算法中的最后一个判断中会将当前所在位置的方格编号从堆栈中删除，之后再弹出的编号就是没被封堵之前的一个方格编号，然后重新进行判断。
实例代码如下:
创建TrceRecord记录路线

package 走迷宫;
//先创建一个记录路线的堆栈
class Node{
	int x;
	int y;
	Node next;
	public Node(int x,int y) {
		this.x=x;
		this.y=y;
		this.next=null;
	}
}
public class TraceRecord {
	public Node first;
	public Node last;
	public boolean isEmpty() {
		return first==null;
	}
	public void insert(int x,int y) {
		Node newNode=new Node(x,y);
		if(this.isEmpty()) {
			first=newNode;
			last=newNode;
		}else {
			last.next=newNode;
			last=newNode;
		}
	}
	public void delete() {
		Node newNode;
		if(this.isEmpty()) {
			System.out.print("[队列已经空了]\n");
			return;
		}
		newNode=first;
		while(newNode.next!=last) {
			newNode=newNode.next;
		}
		newNode.next=last.next;
		last=newNode;
	}
}

在数组地图上开始走迷宫

package 走迷宫;
public class 开始走迷宫 {
	public static int ExitX=8;//定义出口x坐标在第八行
	public static int ExitY=10;//定义出口y坐标在第10列
	public static int[][] MAZE= {{1,1,1,1,1,1,1,1,1,1,1,1},
								 {1,0,0,0,1,1,1,1,1,1,1,1},
								 {1,1,1,0,1,1,0,0,0,0,1,1},
								 {1,1,1,0,1,1,0,1,1,0,1,1},
								 {1,1,1,0,0,0,0,1,1,0,1,1},
								 {1,1,1,0,1,1,0,1,1,0,1,1},
								 {1,1,1,0,1,1,0,1,1,0,1,1},
								 {1,1,1,1,1,1,0,1,1,0,1,1},
								 {1,1,0,0,0,0,0,0,1,0,0,1},
								 {1,1,1,1,1,1,1,1,1,1,1,1}};
	public static void main(String[] args) {
		int i,j,x,y;
		TraceRecord path=new TraceRecord();
		x=1;y=1;
		System.out.print("[迷宫的路径（0标记的部分）]\n");
		for(i=0;i<10;i++) {
			for(j=0;j<12;j++) {
				System.out.print(MAZE[i][j]+"\t");
			}
			System.out.print("\n");
		}
		while(x<=ExitX&&y<=ExitY) {
			MAZE[x][y]=2;
			if(MAZE[x-1][y]==0) {//上走
				x-=1;
				path.insert(x, y);
			}else if(MAZE[x+1][y]==0){//下走
				x+=1;
				path.insert(x, y);
			}else if(MAZE[x][y-1]==0) {//左走
				y-=1;
				path.insert(x, y);
			}else if(MAZE[x][y+1]==0) {//右走
				y+=1;
				path.insert(x, y);
			}else {
				if(chkExit(x,y,ExitX,ExitY)==1) {//判断是否找到出口
					break;
				}else {
					MAZE[x][y]=2;
					path.delete();
					x=path.last.x;
					y=path.last.y;
				}
			}
		}
		System.out.println("[小老鼠走过的路径（2）标记部分]\n");
		for(i=0;i<10;i++) {
			for(j=0;j<12;j++) {
				System.out.print(MAZE[i][j]+"\t");
			}
			System.out.println();
		}
		
	}
	public static int chkExit(int x,int y,int ex,int ey) {
		if(x==ex&&y==ey) {
			return 1;
		}
		return 0;
	}
}

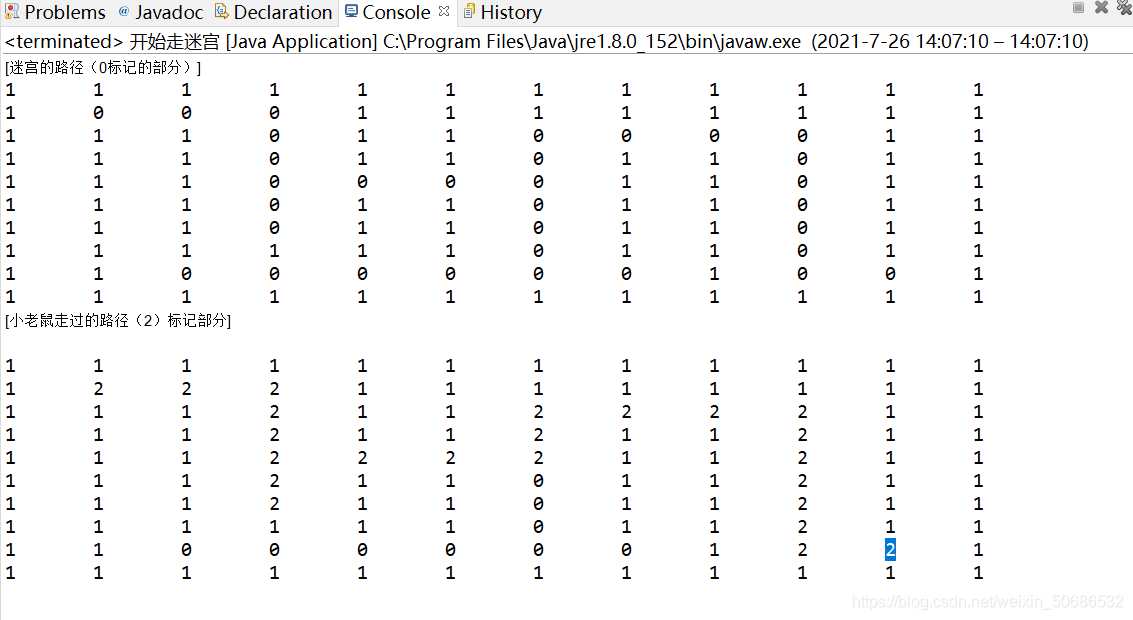
运行结果如下：

8-皇后问题
8-皇后问题也是一种常用的堆栈实例。在国际象棋中的皇后在没有限定一步走几格的前提下，对棋盘中的其他棋子直吃、横吃和对角斜吃（左斜吃或右斜吃都可以）。现在要放入多个皇后到棋盘上，相互之间还不能互相吃到对方。后放入的新皇后后，放入前必须考虑所放位置的直线方向，横线方向是否已经被放置了旧皇后，否则就会被先放入的旧皇后吃掉。
运用上面的规则，我们可以将其应用在44的棋盘中，就称为4-皇后问题。应用在88的棋盘，就称为8-皇后问题。应用在N*N的棋盘，就称为N皇后问题。要解决N-皇后问题（我们以8-皇后为例），首先在棋盘中放入一个新皇后，且这个位置不会被先前放置的皇后吃掉，就将这个新皇后的位置压入堆栈。
但是，如果当放置新皇后的该行（或该列）的8个位置，都没有办法放置新皇后（亦即放入任何一个位置，就会被先前放置的旧皇后吃掉）。此时，就必须从堆栈中弹出前一个皇后的位置，并在该行（或该列）中重新查找到另一个新的位置来放，再将该位置压入堆栈中，而这种方法就是一种回溯算法的应用。
N-皇后问题的解答，就是结合堆栈和回溯两种数据结构，以逐行（或逐列）查找新皇后合适的位置（如果找不到，则回溯到前一行查找前一个皇后的另一个位置，以此类推）的方式，来查找N皇后问题的其中一组解答。
【范例8-皇后问题】

package 八皇后问题;

import java.io.IOException;

public class 八皇后问题 {
	static int TRUE=1,FALSE=0,EIGHT=8;
	static int[] queen=new int[EIGHT];//存放8个皇后之列位置
	static int number=0;//计算共有几组解的总数
	//构造函数
	八皇后问题(){
		number=0;
	}
	//按Enter键函数
	public static void PressEnter() {
		char tChar;
		System.out.print("\n\n");
		System.out.println("...按下Enter键继续....");
		try {
			tChar=(char)System.in.read();
		}catch(IOException e) {};
	}
	//确定皇后存放的位置
	public static void decide_position(int value) {
		int i=0;
		while(i<EIGHT) {
			//是否受到攻击的判断
			if(attack(i,value)!=1) {
				queen[value]=i;
				if(value==7)
					print_table();
				else
					decide_position(value+1);
			}
			i++;
		}
	}
	//测试在（row，col）位置上的皇后是否遭到攻击
	//若遭受攻击则返回值为1，否则返回0
	public static int attack(int row,int col) {
		int i=0,atk=FALSE;
		int offset_row=0,offset_col=0;
		while((atk!=1)&&i<col) {
			offset_col=Math.abs(i-col);
			offset_row=Math.abs(queen[i]-row);
			//判断两个皇后是否在同一行或者同一对角线上
			if((queen[i]==row)||(offset_row==offset_col)) {
				atk=TRUE;
				
			}
			i++;
		}
		return atk;
	}
	//输出需要的结果
	public static void print_table() {
		int x=0,y=0;
		number+=1;
		System.out.println();
		System.out.print("8-皇后问题的第"+number+"组解\n\t");
		for(x=0;x<EIGHT;x++) {
			for(y=0;y<EIGHT;y++) {
				if(x==queen[y]) {
					System.out.print("<*>");
				}else {
					System.out.print("<->");
				}
			}
		System.out.print("\n\t");}
		PressEnter();
	}
	public static void main(String[] args) {
		八皇后问题 bhhwt=new 八皇后问题();
		bhhwt.decide_position(0);
	}
}

运行结果如下：