2019年蓝桥杯省赛 C++ A组

A.平方和

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+5;
ll sum=0;
bool check(int x){
	while(x){
		int t=x%10;
		if(t==2||t==0||t==1||t==9) return true;
		x/=10;
	}
	return false;
}
int main(){
	for(int i=1;i<=2019;i++){
		if(check(i)) sum+=i*i;
	}
	cout<<sum;
} 

---

B.数列求值

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=3e7+5,mod=1e4;
int f[N];
int main(){
	f[1]=f[2]=f[3]=1;
	for(int i=4;i<=20190324;i++){
		f[i]=(f[i-1]+f[i-2]+f[i-3])%mod;
	}
	cout<<f[20190324];
} 

---

C.最大降雨量

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=3e7+5,mod=1e4;
int res;
int main(){
	int n=49;
	//每周用三个最小的，三个最大的 
	//后三周 
	for(int i=1;i<=3;i++){
		n-=4;
	}
	//第三周 
	n-=3; 
	cout<<n;
} 

---

D.迷宫

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
typedef pair<PII,string> PIS;
const int N=55;
int res;
bool vis[N][N];
int dx[]={1,0,0,-1},dy[]={0,-1,1,0};
char c[]={'D','L','R','U'};
int n=30,m=50;
char g[N][N];
int main(){
	freopen("maze.txt","r",stdin);
	for(int i=1;i<=n;i++){
		cin>>g[i]+1;
	}
	queue<PIS> q;
	q.push({{1,1},""});
	vis[1][1]=true;
	while(!q.empty()){
		PIS t=q.front();q.pop();
		int x=t.first.first,y=t.first.second;
		string path=t.second;
		if(x==n&&y==m){
			cout<<path;
			break;
		}
		for(int i=0;i<4;i++){
			int nx=x+dx[i],ny=y+dy[i];
			if(nx<1||ny<1||nx>n||ny>m) continue;
			if(g[nx][ny]=='1') continue;
			if(vis[nx][ny]) continue;
			vis[nx][ny]=true;
			q.push({{nx,ny},path+c[i]});
		}
	}
	//cout<<"DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR";
} 

---

E.RSA解密

---

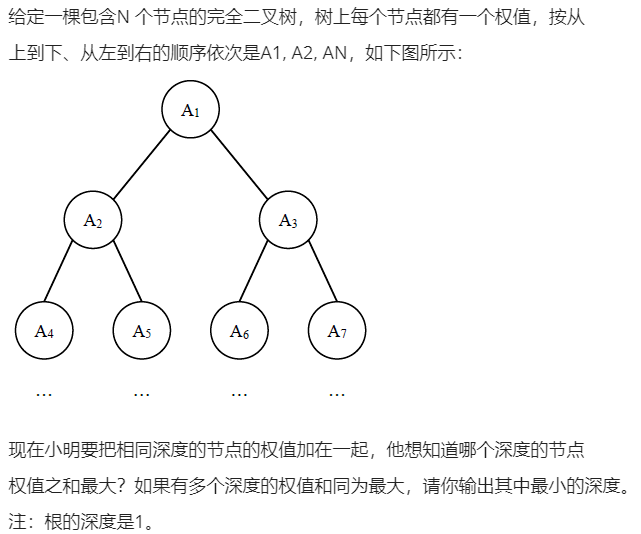
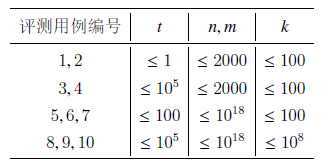
F.完全二叉树的权值（二叉树）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+5;
int res;
ll maxn=-1e18;
int main(){
    int n;cin>>n;
    int d=1;
    for(int i=1,h=1;i<=n;h++,d*=2){
        ll sum=0;
        int cnt=d;
        while(cnt--&&i<=n){
            int x;cin>>x;
            sum+=x;
            i++; 
        }
        if(sum>maxn){
            maxn=sum;
            res=h;
        }
    }
    cout<<res;
} 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+5;
int res;
ll maxn=-1e18;
ll w[N];
int main(){
	int n;cin>>n;
	for(int i=1;i<=n;i++){
		cin>>w[i];
		w[i]+=w[i-1];
	}
	int l=1,r=1,d=1;
	while(r<=n){
		if(w[r]-w[l-1]>maxn){
			maxn=w[r]-w[l-1];
			res=d;
		}
		l=2*l,r=2*r+1;
		d++;
	}
	if(l<=n){
		if(w[n]-w[l-1]>maxn){
			maxn=w[n]-w[l-1];
			res=d;
		}
	}
	cout<<res;
} 

---

G.外卖店优先级（模拟）

        注意：对于一个订单的操作顺序，要先减去间隔时间带来的优先级衰减，然后判断是否要剔除，再加上订单的优先级收益，最后判断是否要加入

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+5;
struct node{
	int t,id;
	bool operator<(const node& a) const{
		return t<a.t;
	}
}w[N];
int n,m,T;
bool vis[N];//在缓存
int cnt[N];//优先级
int last[N];//上次被访问时间 
int main(){
	cin>>n>>m>>T;
	for(int i=1;i<=m;i++){
		int t,id;cin>>t>>id;
		w[i]={t,id};
	}
	sort(w+1,w+m+1);
	for(int i=1;i<=m;i++){
		int t=w[i].t,id=w[i].id;
		if(t!=last[id]) cnt[id]-=(t-last[id]-1);
		cnt[id]=max(cnt[id],0);
		//先判断是否要移除，然后再加 
		if(vis[id]&&cnt[id]<=3) vis[id]=false;
		cnt[id]+=2;
		if(!vis[id]&&cnt[id]>5) vis[id]=true;
		last[id]=t;
	}
	int res=0;
	for(int i=1;i<=n;i++){
		if(T!=last[i]) cnt[i]-=(T-last[i]);
		cnt[i]=max(cnt[i],0);
		if(vis[i]&&cnt[i]<=3) vis[i]=false;
		if(vis[i]) res++;
	}
	cout<<res;
} 

---

H.修改数组 （线段树 / 并查集）

线段树解法：对于w[i]，查w[i]~M区间维护的最小值即可 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=1e5+5,M=1e6+N;
int n;
int w[N];
struct node{
	int l,r;
	int minn;
}tr[M<<2];
void pushup(int u){
	tr[u].minn=min(tr[u<<1].minn,tr[u<<1|1].minn);
}
void build(int u,int l,int r){
	if(l==r){
		tr[u]={l,r,l};
	}else{
		tr[u]={l,r};
		int mid=l+r>>1;
		build(u<<1,l,mid);
		build(u<<1|1,mid+1,r);
		pushup(u);
	}
}
int query(int u,int l,int r){
	if(tr[u].l>=l&&tr[u].r<=r) return tr[u].minn;
	int mid=tr[u].l+tr[u].r>>1;
	int res=0x3f3f3f3f;
	if(l<=mid) res=min(res,query(u<<1,l,r));
	if(r>mid) res=min(res,query(u<<1|1,l,r));
	return res;
}
void modify(int u,int x,int c){
	if(tr[u].l==tr[u].r&&tr[u].l==x){
		tr[u].minn=c;
		return;
	}
	int mid=tr[u].l+tr[u].r>>1;
	if(x<=mid) modify(u<<1,x,c);
	if(x>mid) modify(u<<1|1,x,c);
	pushup(u);
}
int main(){
	cin>>n;
	build(1,1,M-5);
	for(int i=1;i<=n;i++){
		cin>>w[i];
		int res=query(1,w[i],M-5);
		w[i]=res;
		modify(1,res,0x3f3f3f3f);
	}
	for(int i=1;i<=n;i++){
		cout<<w[i];
		if(i!=n) cout<<" ";
	}
} 

并查集解法：p[x]指向的是  如果下一次遇到x  应该修改成的数，在find的过程中，其实就是找到第一个没有出现过的数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+5;
int p[N];
int w[N];
int find(int x){
	if(p[x]!=x) p[x]=find(p[x]);
	return p[x];
} 
int main(){
	int n;cin>>n;
	for(int i=1;i<=n;i++) cin>>w[i];
	for(int i=1;i<=N;i++) p[i]=i;
	for(int i=1;i<=n;i++) {
		int x=find(w[i]);
		cout<<x;
		p[x]=x+1;//p[x]指向的就是x应该修改成的数
		if(i!=n) cout<<" ";
	}
} 

---

I.糖果（搜索 / 状压DP）

普通搜索解法： N<=100，不能直接根据选/不选某包糖果进行搜索，但是M<=20，可以尝试根据口味进行搜索（理论上会超时一部分）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=105,M=25;
int n,m,k;
vector<int> vc[M];//vc[i] 拥有糖果i的 包裹集合 
int bag[N];//包裹i拥有的糖果状态 
int res=0x3f3f3f3f;
//第u个口味，已经拿了cnt包 目前有的糖果情况为g 
void dfs(int u,int cnt,int g){
	if(cnt>=res) return;
	if(u==m+1){
		res=cnt;
		return;
	}
	if(g>>u&1){
		dfs(u+1,cnt,g);
		return;
	}
	for(int i=0;i<vc[u].size();i++){
		int t=vc[u][i];
		dfs(u+1,cnt+1,g|bag[t]);
	}
}
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=k;j++){
			int x;cin>>x;
			vc[x].push_back(i);
			if(bag[i]>>x&1) continue;
			bag[i]+=1<<x;
		}
	}
	dfs(1,0,0);
	if(res==0x3f3f3f3f) res=-1;
	cout<<res;
} 

IDA*解法：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=105,M=1<<20;
vector<int> vc[N];//vc[i] 包含i这个口味的所有状态 
int n,m,k;
int lg2[M];
//IDA* 
int lowbit(int x)
{
	return x&-x;
}
int h(int st)//估价函数 
{
	int res=0;//当前状态st还需要取的包裹数量 
	for(int i=(1<<m)-1-st;i;i-=lowbit(i))
	{ 
		int c=lg2[lowbit(i)];
		res++;
		for(int j=0;j<vc[c].size();j++)
		{
			int g=vc[c][j];
			i&=~g;//将状态g里的1 对应i里的1清空 
		}
	} 
	return res; 
} 
bool dfs(int depth,int st)
{
	//搜索完n层（取了n个包裹） 或者  当前需要取的包裹个数大于剩余可取个数 
	if(!depth||h(st)>depth)
	{
		if(st==(1<<m)-1)//所有的口味都得到 
			return true;
		return false;
	}
	int t=-1;
	//枚举此状态下，所有未得到的口味中，选择最少的那种方案 
	for(int i=(1<<m)-1-st;i;i-=lowbit(i))
	{ 
		int c=lg2[lowbit(i)];//包裹编号
		if(t==-1||vc[t].size()>vc[c].size())
			t=c; 
	} 
	for(int i=0;i<vc[t].size();i++)
	{//枚举对于这种口味的所有选择 
		int g=vc[t][i];//选择的状态 
		if(dfs(depth-1,st|g))//寻找下一层 
			return true;
	}
	return false;
}
int main()
{
	cin>>n>>m>>k;
	for(int i=0;i<m;i++) lg2[1<<i]=i; 
	for(int i=1;i<=n;i++)
	{
		int st=0;
		for(int j=0;j<k;j++)
		{
			int x;cin>>x;
			st|=1<<x-1;//状态中0~m-1位 表示 第1~m个口味 
		}
		for(int j=0;j<m;j++)
			if(st>>j&1) 
				vc[j].push_back(st);
	}
	int depth=0;//这里的迭代深度代表的就是选择包裹个数 
	while(depth<=m&&!dfs(depth,0))
		depth++;
	if(depth>m) cout<<-1;
	else cout<<depth;
		
}

状压DP解法：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=105,M=25;
int n,m,k;
int bag[N];
int f[1<<21];//f[i][j] 前i个选，选的糖果状态为j的最小个数 
int main(){
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=k;j++){
			int x;cin>>x;
			bag[i]|=1<<x-1;
		}
	}
	memset(f,0x3f,sizeof f);
	f[0]=0;
	for(int i=1;i<=n;i++){
		for(int j=0;j<1<<m;j++){
			f[j|bag[i]]=min(f[j|bag[i]],f[j]+1);
		}
	} 
	if(f[(1<<m)-1]==0x3f3f3f3f) cout<<-1<<endl;
    else cout<<f[(1<<m)-1]<<endl;
} 

---

J.组合数问题（Lucas定理）