华为面试题及答案——机器学习(二)

21. 如何评价分类模型的优劣?

（1）模型性能指标

1. 准确率（Accuracy）：

   • 定义：正确分类的样本数与总样本数之比。
   • 适用：当各类样本的数量相对均衡时。

2. 精确率（Precision）：

   • 定义：预测为正类的样本中实际为正类的比例。
   • 适用：当关注假阳性错误的成本较高时（例如垃圾邮件检测）。

3. 召回率（Recall）：

   • 定义：实际为正类的样本中被正确预测为正类的比例。
   • 适用：当关注假阴性错误的成本较高时（例如疾病检测）。

4. F1得分（F1 Score）：

   • 定义：精确率和召回率的调和平均数。
   • 适用：当需要平衡精确率和召回率时。

5. ROC曲线（Receiver Operating Characteristic Curve）和AUC（Area Under the Curve）：

   • 定义：ROC曲线是以假阳性率为横轴、真正率为纵轴绘制的曲线，AUC是该曲线下的面积。
   • 适用：用于评估模型在不同阈值下的表现。

6. PR曲线（Precision-Recall Curve）和AUC-PR：

   • 定义：PR曲线是以召回率为横轴、精确率为纵轴绘制的曲线，AUC-PR是该曲线下的面积。
   • 适用：特别适合于类别不平衡的情况。

（2）其他考虑因素

1. 模型复杂度：

   • 简单模型（如线性模型）易于理解和解释，但可能无法捕捉复杂的模式。
   • 复杂模型（如深度神经网络）能够捕捉复杂模式，但可能难以解释和调试。

2. 训练时间和推理时间：

   • 训练时间：模型从数据中学习的时间。复杂模型通常需要更长的训练时间。
   • 推理时间：模型进行预测的时间。在实时应用中，较短的推理时间是优点。

3. 模型的可解释性：

   • 可解释性：模型结果的透明度和理解度。在某些领域，如医疗和金融，可解释性是非常重要的。

4. 鲁棒性和稳定性：

   • 鲁棒性：模型应对噪声和异常值的能力。
   • 稳定性：模型在不同的数据集或样本上的一致性表现。

（3）综合评价

1. 交叉验证：

   • 使用交叉验证（如k折交叉验证）可以更可靠地评估模型性能，减少过拟合的影响。

2. 混淆矩阵：

   • 通过混淆矩阵（Confusion Matrix）可以详细了解模型的分类错误类型，包括真阳性、真阴性、假阳性和假阴性。

3. 业务目标和应用场景：

   • 根据具体的业务目标和应用场景选择合适的评价指标和模型。例如，在医疗诊断中，召回率可能比准确率更重要。

（4）实际应用中的权衡

在实际应用中，通常需要在不同的评价指标之间进行权衡。例如：

• 在类别不平衡的情况下，更倾向于使用F1得分、AUC-PR等指标。
• 对于需要实时预测的应用，更关注模型的推理时间。
• 在高度监管的领域（如金融或医疗），模型的可解释性可能比纯粹的性能指标更重要。

22.如何评价回归模型的优劣 ?

• 均方误差（Mean Squared Error, MSE）：

  • 定义：预测值与实际值之间的平方差的平均值。
  • 公式：

            

• • 适用：当对较大的误差较为敏感时。

• 均方根误差（Root Mean Squared Error, RMSE）：

  • 定义：MSE的平方根。
  • 公式：
  • 
  • 适用：与MSE类似，但与原数据单位一致，更易于解释。

• 平均绝对误差（Mean Absolute Error, MAE）：

  • 定义：预测值与实际值之间绝对差的平均值。
  • 公式：

               

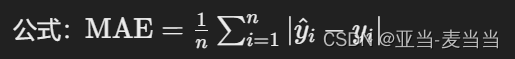
• • 适用：当对所有误差同等看待时。

• 决定系数（R² Score）：

  • 定义：衡量模型解释数据变异的能力，取值范围为0到1。
  • 公式：

       

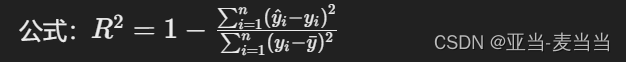
• 适用：反映模型的整体解释能力，但不适用于非线性关系或异方差性的情况。

• 调整决定系数（Adjusted R²）：

  • 定义：对R²进行调整，以惩罚使用过多的特征。
  • 适用：当模型有较多特征时，防止过拟合。

23.有哪些处理样本不均衡问题的处理方法 ?

（1）数据层面的处理方法

1. 欠采样（Under-sampling）：

   • 方法：从多数类中随机选择一部分样本，使其数量与少数类样本相等或接近。
   • 优点：简单易行，可以有效平衡数据集。
   • 缺点：可能丢失有用的信息，导致模型性能下降。

2. 过采样（Over-sampling）：

   • 方法：通过重复少数类样本或生成新的少数类样本，使其数量增加到与多数类样本相等或接近。
   • 常用技术：
     • 随机过采样：简单地重复少数类样本。
     • SMOTE（Synthetic Minority Over-sampling Technique）：通过插值生成新的少数类样本。
     • ADASYN（Adaptive Synthetic Sampling）：改进的SMOTE，根据少数类样本的分布自适应生成新样本。
   • 优点：增加少数类样本，丰富数据集。
   • 缺点：可能导致过拟合，尤其是随机过采样。

3. 组合采样（Combined Sampling）：

   • 方法：结合过采样和欠采样，既减少多数类样本又增加少数类样本。
   • 优点：可以在不丢失太多信息的情况下平衡数据集。
   • 缺点：需要选择合适的过采样和欠采样比例。

（2）算法层面的处理方法

1. 调整分类阈值：

   • 方法：通过调整分类器的决策阈值，使得模型更倾向于预测少数类。
   • 优点：简单易行，不需要更改数据。
   • 缺点：需要手动调整和选择最佳阈值。

2. 代价敏感学习（Cost-sensitive Learning）：

   • 方法：在训练过程中对少数类样本赋予更高的权重，或者在损失函数中对不同类别设置不同的代价。
   • 优点：直接在模型训练过程中处理不平衡问题。
   • 缺点：需要确定合适的代价权重。

3. 集成方法（Ensemble Methods）：

   • Bagging和Boosting：可以通过对样本进行重采样（如Bagging）或调整样本权重（如Boosting）来处理不平衡问题。
   • Balanced Random Forest：在随机森林中，通过欠采样多数类或过采样少数类来平衡每棵决策树的训练集。
   • EasyEnsemble和BalanceCascade：分别通过多次欠采样和级联欠采样来构建集成模型。
   • 优点：可以通过多次采样和集成模型提高整体性能。
   • 缺点：计算开销较大。

24. 为什么会发生过拟合和欠拟合，怎么解决模型的过拟合和欠拟合的问题 ?

过拟合和欠拟合是机器学习模型在训练和预测过程中常见的问题。理解它们的原因和解决方法对于构建高效和鲁棒的模型至关重要。

（1）过拟合和欠拟合的原因

过拟合（Overfitting）

原因：

1. 模型复杂度高：模型有太多的参数或复杂度太高，能够记住训练数据中的噪声和异常值。
2. 训练数据不足：训练数据量不足以支撑复杂模型，模型会倾向于记住而不是泛化。
3. 训练时间过长：模型训练时间过长，过度拟合训练数据。
4. 特征选择不当：包括了太多无关或冗余的特征，使模型在训练数据上表现很好，但在新数据上表现不佳。

欠拟合（Underfitting）

原因：

1. 模型复杂度低：模型太简单，不能捕捉数据中的潜在模式。
2. 特征不足：缺乏足够的或适当的特征来描述数据的结构。
3. 训练时间不足：模型训练时间不够，未能充分学习数据的模式。
4. 错误的模型假设：模型的假设（如线性假设）不符合数据的实际分布。

（2）解决过拟合和欠拟合的方法

解决过拟合的方法

1. 正则化（Regularization）：

   • L1正则化（Lasso）和L2正则化（Ridge）：在损失函数中加入正则项，惩罚大幅度的参数。
   • 弹性网络（Elastic Net）：结合L1和L2正则化的优点。

2. 交叉验证（Cross-validation）：

   • 使用k折交叉验证来选择最优模型参数，防止模型过拟合。

3. 剪枝（Pruning）（适用于决策树）：

   • 移除或修剪掉决策树中的冗余节点，以减少模型复杂度。

4. 早停（Early Stopping）：

   • 在验证误差开始增大时停止训练，防止模型在训练数据上过拟合。

5. 数据增强（Data Augmentation）：

   • 通过数据增强技术（如旋转、缩放、裁剪等）生成更多的训练样本，特别适用于图像数据。

6. 减少特征数量：

   • 通过特征选择或降维技术（如PCA）减少特征数量，减少模型复杂度。

7. 增加训练数据：

   • 获取更多的训练数据，以使模型能够更好地泛化。

解决欠拟合的方法

1. 增加模型复杂度：

   • 使用更复杂的模型（如从线性回归转到多项式回归或深度神经网络）。

2. 增加特征：

   • 添加更多相关特征或使用特征工程提取更有用的特征。

3. 训练更长时间：

   • 允许模型训练更长时间，以充分学习数据中的模式。

4. 减少正则化力度：

   • 减少正则化参数，以允许模型学习更多的数据细节。

5. 选择合适的模型：

   • 根据数据的性质选择更合适的模型。例如，对于非线性数据，选择非线性模型（如支持向量机、神经网络等）。

6. 调整模型参数：

   • 通过超参数调优（如网格搜索、随机搜索）找到最佳模型参数。

25. 解释一下什么是偏差和方差和泛化误差

偏差（Bias）

偏差是指模型预测值与真实值之间的系统性误差。偏差反映了模型在训练数据上的拟合能力，即模型对数据中模式的捕捉能力。高偏差通常意味着模型过于简单，不能很好地捕捉数据的复杂关系。

• 低偏差：模型能够较好地拟合训练数据，捕捉数据中的模式。
• 高偏差：模型对数据中的模式捕捉不足，通常表现为欠拟合。

方差（Variance）

方差是指模型预测结果随训练数据变化而变化的程度。方差反映了模型对训练数据中的细节和噪声的敏感程度。高方差通常意味着模型过于复杂，过度拟合训练数据中的噪声和异常值。

• 低方差：模型对训练数据中的噪声不敏感，预测结果稳定。
• 高方差：模型对训练数据中的细节和噪声过于敏感，通常表现为过拟合。

泛化误差（Generalization Error）

泛化误差是指模型在新数据（未见过的数据）上的预测误差。它反映了模型的泛化能力，即模型从训练数据中学习到的模式在新数据上的表现。泛化误差由以下两个部分组成：

1. 偏差：模型对真实模式的捕捉能力。如果模型过于简单（高偏差），泛化误差会较高。
2. 方差：模型对训练数据的敏感程度。如果模型过于复杂（高方差），泛化误差也会较高。

26. 聚类模型有哪些 ?

1. K-means 聚类

• 原理：将数据分为K个簇，每个簇由一个中心点（质心）表示，通过迭代优化使得每个数据点到其最近质心的距离之和最小。
• 优点：简单、计算效率高。
• 缺点：需要预先指定簇数K，对初始质心敏感，适合球状分布的数据。

2. 层次聚类（Hierarchical Clustering）

• 原理：通过构建层次树状结构（树状图）来聚类数据，分为凝聚层次聚类（自底向上）和分裂层次聚类（自顶向下）。
• 优点：不需要预先指定簇数，可以生成层次结构。
• 缺点：计算复杂度高，尤其是对大数据集。

3. DBSCAN（Density-Based Spatial Clustering of Applications with Noise）

• 原理：基于密度的聚类方法，通过找到高密度区域来形成簇，能自动识别噪声点。
• 优点：能发现任意形状的簇，自动识别噪声，不需要预先指定簇数。
• 缺点：对参数选择敏感（如最小样本数和邻域半径），对数据集的密度变化敏感。

4. 均值漂移（Mean Shift）

• 原理：通过平移点到高密度区域的均值点来形成簇，直到所有点收敛到密度峰值。
• 优点：不需要预先指定簇数，能够发现任意形状的簇。
• 缺点：计算复杂度高，尤其是对大数据集。

5. 高斯混合模型（Gaussian Mixture Model, GMM）

• 原理：假设数据是由多个高斯分布组成的，通过期望最大化（EM）算法来估计参数，进而进行聚类。
• 优点：能够处理协方差不同的簇，适用于高斯分布的数据。
• 缺点：需要预先指定簇数，对初始参数选择敏感。

6. 光谱聚类（Spectral Clustering）

• 原理：利用数据的相似度矩阵，通过谱分解得到数据的低维表示，再使用K-means等方法进行聚类。
• 优点：能够处理复杂形状的簇，适用于高维数据。
• 缺点：计算复杂度高，尤其是相似度矩阵的构建和谱分解过程。

7. OPTICS（Ordering Points To Identify the Clustering Structure）

• 原理：类似于DBSCAN，但能够发现不同密度的簇，通过生成可视化的聚类顺序图来识别簇。
• 优点：能够处理不同密度的簇，不需要预先指定簇数。
• 缺点：计算复杂度高，对参数选择敏感。

8. BIRCH（Balanced Iterative Reducing and Clustering using Hierarchies）

• 原理：通过构建树状结构（CF树）来逐步聚类大数据集，适合处理大规模数据。
• 优点：适合大规模数据，能够动态更新。
• 缺点：对簇的形状和大小有一定的假设，可能需要后处理步骤。

9. 领域自适应传播（Affinity Propagation）

• 原理：通过发送消息在数据点之间进行簇中心的选择，不需要预先指定簇数。
• 优点：不需要预先指定簇数，能够发现簇中心。
• 缺点：计算复杂度高，对参数选择敏感。

10. 随机森林聚类（Random Forest Clustering）

• 原理：利用随机森林生成数据的相似度矩阵，再通过聚类算法进行聚类。
• 优点：适用于高维数据，能够处理复杂的簇结构。
• 缺点：计算复杂度高，需要生成相似度矩阵。

27. k-means聚类的k如何确定 ?

• 肘部法（Elbow Method）：

  • 计算不同 KKK 值下的总簇内平方和（Within-cluster Sum of Squares, WCSS）。
  • 画出 KKK 值和 WCSS 的图，当图中 WCSS 随 KKK 的增加开始呈现平缓下降时，拐点（“肘部”）对应的 KKK 值即为最佳 KKK 值。

• 轮廓系数（Silhouette Score）：

  • 轮廓系数结合了簇内紧密度和簇间分离度。
  • 计算不同 KKK 值下的轮廓系数，选择轮廓系数最高的 KKK 值。

• 加权平均信息准则（AIC, BIC）：

  • 使用高斯混合模型（GMM）进行聚类，并计算不同 KKK 值下的 AIC 或 BIC。
  • 选择 AIC 或 BIC 最小的 KKK 值。

• 跨验证法（Cross-validation）：

  • 使用交叉验证技术，通过划分训练集和验证集，计算不同 KKK 值下的聚类性能，选择验证集上表现最好的 KKK 值。

• 专家知识：

  • 基于对数据的先验知识，选择可能合理的 KKK 值。

28.k-means聚类的优缺点 ?

优点：

1. 简单易行：算法实现简单，易于理解和实现。
2. 计算效率高：适合处理大规模数据集，时间复杂度为 O(n⋅k⋅t)O(n \cdot k \cdot t)O(n⋅k⋅t)（其中 nnn 是样本数量，kkk 是簇数，ttt 是迭代次数）。
3. 收敛速度快：在多数情况下，算法能够快速收敛到一个局部最优解。

缺点：

1. 需要预先指定 KKK 值：必须事先指定簇数 KKK，不总是容易确定最佳 KKK 值。
2. 对初始值敏感：初始质心的选择会影响最终聚类结果，可能导致局部最优。
3. 适用于球形簇：假设簇是球形且大小相似，对于复杂形状的簇效果较差。
4. 易受异常值影响：异常值可以显著影响质心的位置，从而影响聚类结果。
5. 适用于均匀分布数据：对于密度不均的数据效果不好。

29.k-means聚类和层次聚类的差异 ?

方法和步骤：

1. K-means 聚类：

   • 初始化：选择 KKK 个初始质心。
   • 迭代：分配每个样本到最近的质心，更新质心位置，直到收敛。
   • 适用场景：适合大规模数据，数据点数量较多时效果较好。

2. 层次聚类：

   • 凝聚层次聚类（自底向上）：每个样本开始时是一个单独的簇，逐步合并最近的簇，直到只剩下一个簇或达到预定的簇数。
   • 分裂层次聚类（自顶向下）：所有样本开始时是一个簇，逐步分裂成更小的簇，直到每个样本是一个单独的簇或达到预定的簇数。
   • 适用场景：适合小规模数据，能生成层次树状结构，有助于理解数据结构。

优缺点：

1. K-means 聚类：

   • 优点：计算效率高，适合大规模数据。
   • 缺点：需要预先指定 KKK 值，对初始质心和异常值敏感。

2. 层次聚类：

   • 优点：不需要预先指定簇数，生成层次结构，易于解释。
   • 缺点：计算复杂度高，尤其是对大数据集，合并或分裂步骤不易调整。

计算复杂度：

1. K-means 聚类：时间复杂度为 O(n⋅k⋅t)O(n \cdot k \cdot t)O(n⋅k⋅t)，适合大规模数据。
2. 层次聚类：时间复杂度通常为 O(n3)O(n^3)O(n3)，不适合大规模数据。

适用数据类型：

1. K-means 聚类：适合均匀分布的球形簇，不适合复杂形状的簇。
2. 层次聚类：适合任意形状的簇，可以生成层次结构，但计算效率较低。

30.k-means聚类如何更好地规避初始点的选择对模型造成的误差 ?

K-means 聚类对初始质心的选择非常敏感，导致不同的初始点可能产生不同的聚类结果。为规避这种问题，可以采用以下方法：

1. K-means++ 初始化：

   • 方法：K-means++ 通过一种聪明的初始化策略选择初始质心，以增加不同质心之间的距离，减少不良初始点带来的影响。
   • 步骤：首先随机选择一个质心，然后根据距离选择剩余的质心，使得新质心尽量远离已选择的质心。

2. 多次运行取最优：

   • 方法：多次运行 K-means 聚类算法，每次用不同的随机初始质心，最后选择总误差最小的结果。
   • 优点：增加了找到全局最优解的机会。

3. 层次聚类的结果作为初始质心：

   • 方法：先用层次聚类方法聚类，然后用聚类结果中的中心点作为 K-means 的初始质心。
   • 优点：层次聚类可以提供较好的初始点。

4. 密度聚类的结果作为初始质心：

   • 方法：先用密度聚类方法（如 DBSCAN）找到密度高的区域，然后用这些区域的中心点作为 K-means 的初始质心。
   • 优点：密度聚类能够识别出数据集中的高密度区域作为初始点，有助于提高 K-means 的效果。

31. k-means 聚类 和DBSCAN 模型的差异和优缺点

K-means 聚类：

• 优点：
  • 计算效率高，适合大规模数据。
  • 简单易行，容易实现和理解。
• 缺点：
  • 需要预先指定簇数 KKK。
  • 对初始质心敏感，容易陷入局部最优。
  • 适合球形且大小相似的簇，不适合复杂形状的簇。
  • 对异常值敏感。

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）：

• 优点：
  • 能够发现任意形状的簇。
  • 不需要预先指定簇数。
  • 能自动识别噪声点（异常值）。
  • 适合处理密度不均的数据。
• 缺点：
  • 对参数（如最小样本数和邻域半径）敏感，参数选择不当可能导致聚类效果差。
  • 计算复杂度较高，特别是在大规模数据集上。

32. PCA 是什么 ?

        PCA（Principal Component Analysis，主成分分析）是一种降维技术，用于将高维数据转换为低维数据，同时尽可能保留数据的主要特征。PCA 通过线性变换将数据投影到新的坐标系上，这些新坐标系的轴称为主成分，按方差大小排序。前几个主成分包含了数据中最多的信息量。

33. 如何确定PCA保留几个主成分 ?

• 累计方差解释率：

  • 计算每个主成分的方差解释率，累加方差解释率，直到达到预定阈值（如 95% 或 99%）。
  • 方法：选择累计解释率达到阈值所需的最少主成分数。

• 碎石图（Scree Plot）：

  • 画出主成分的方差解释率与主成分数的图，寻找“肘部”位置。
  • 方法：选择在图中解释率曲线开始平缓的点之前的主成分数。

• 实际应用需要：

  • 根据具体应用场景和需要的特征数，选择合适的主成分数。

34.PCA一般在什么场景下使用 ?

• 降维：
  • 高维数据降维为低维数据，以减少计算复杂度和存储空间。
• 特征提取：
  • 提取主要特征，保留数据的主要信息，提高后续机器学习模型的性能。
• 数据可视化：
  • 将高维数据转换为二维或三维数据，以便于可视化和理解数据结构。
• 噪声去除：
  • 去除数据中的噪声，保留主要信息，提高数据质量。

35. LDA(Linear Discriminant Analysis) 和PCA的差异?

PCA（主成分分析）：

• 目标：通过最大化数据在主成分上的方差，实现无监督的降维。
• 应用场景：用于无标签数据的降维，强调数据的全局方差。
• 方法：通过特征值分解协方差矩阵，找到最大方差方向的主成分。
• 适用性：主要用于数据降维和特征提取，不考虑类别标签。

LDA（线性判别分析）：

• 目标：通过最大化类间方差与类内方差之比，实现有监督的降维和分类。
• 应用场景：用于有标签数据的降维，强调类别之间的可分性。
• 方法：通过特征值分解类内散度矩阵和类间散度矩阵的比值，找到最能区分不同类别的方向。
• 适用性：主要用于分类任务的数据降维和特征提取，考虑类别标签。

主要区别：

• 是否有监督：PCA 是无监督方法，LDA 是有监督方法。
• 目标不同：PCA 最大化方差，LDA 最大化类间方差与类内方差之比。
• 用途不同：PCA 主要用于降维和特征提取，LDA 主要用于分类任务的数据降维。