数据结构单链表——一元多项式求和（C语言版）

这里测试用例有很多的坑
我是一点点改出来的：

1. 输入的多项式正负全抵消，输出是一个0，而不是多个0
2. 输入的多项式其中一个为-1，-1，即为空
3. 输入的多项式两个都为-1，-1时，结果为0

我的思路是在A链表的基础上进行修改：
1.当A和B的系数相等，就直接修改A的数值

 if (pA->zhishu == pB->zhishu)
 {
     pA->xishu += pB->xishu;
     preA = pA;
     pA = pA->next;
     pB = pB->next;
 }

2.当A的系数大于B的系数，就让A的指针往后移

 else if (pA->zhishu > pB->zhishu)
 {
     preA = pA;
     pA = pA->next;
 }

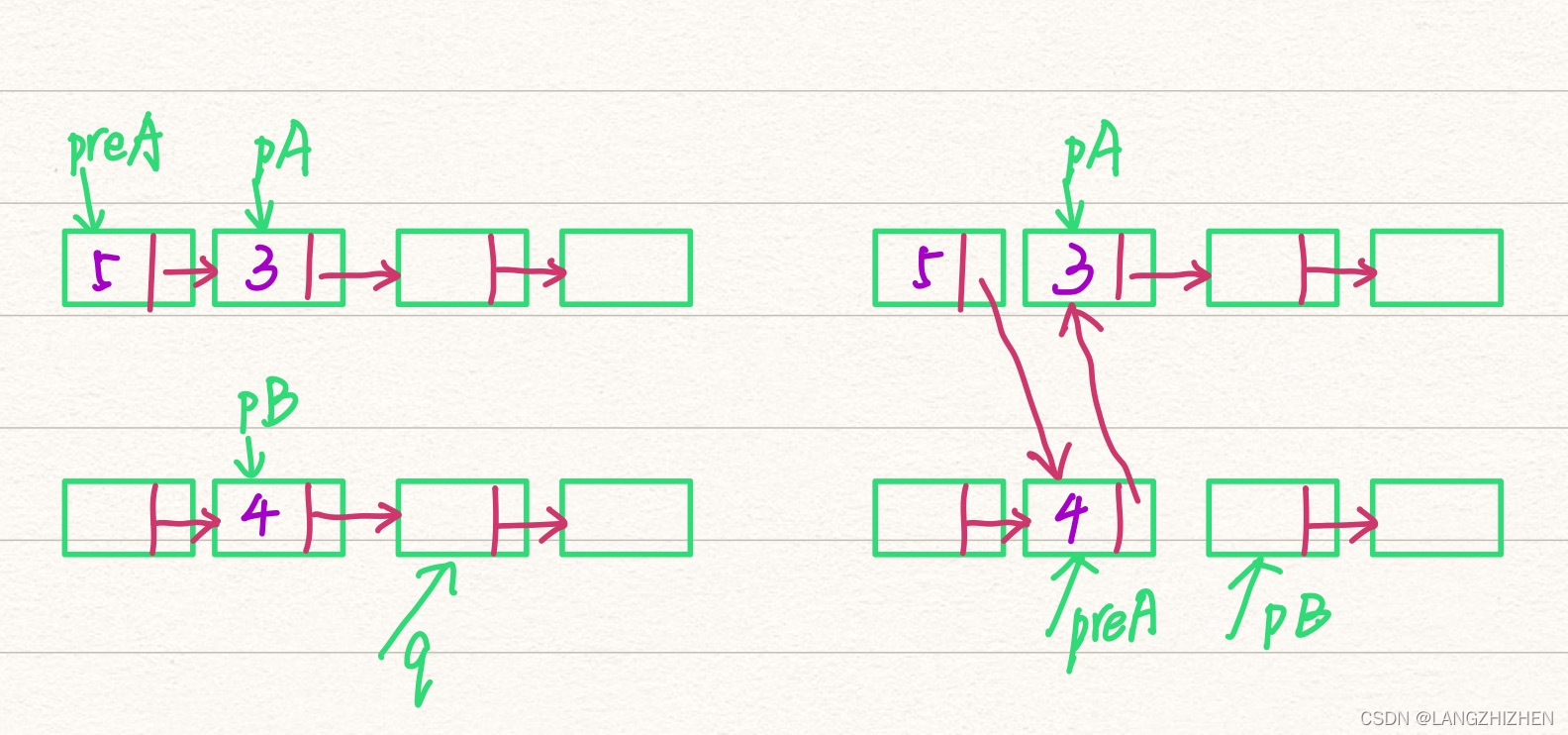
3.当A的系数小于B的系数，此时B节点应该插在A节点前面，所以我们需要设置一个保存A的前驱节点的指针preA

else
{
    LNode *q = pB->next;
    preA->next = pB;
    preA = pB;
    pB->next = pA;
    pB = q;
}

同时因为pB->next = pA这条语句会使原pB丢失连接，所以我们需要一个指针q来保存pB->next的连接。如图所示：

直接上代码：

#include <stdio.h>
#include <stdlib.h>
typedef struct LNode
{
    int xishu;
    int zhishu;
    LNode *next;
} LNode, *LinkedList;
void PolySum(LinkedList &A, LinkedList B)
{
    LNode *pA = A->next;
    LNode *preA = A;
    LNode *pB = B->next;
    while (pA != nullptr && pB != nullptr)
    {
        if (pA->zhishu == pB->zhishu)
        {
            pA->xishu += pB->xishu;
            preA = pA;
            pA = pA->next;
            pB = pB->next;
        }
        else if (pA->zhishu > pB->zhishu)
        {
            preA = pA;
            pA = pA->next;
        }
        else
        {
            LNode *q = pB->next;
            preA->next = pB;
            preA = pB;
            pB->next = pA;
            pB = q;
        }
    }
    while (pB != nullptr)
    {
        preA->next = pB;
        preA = pB;
        pB = pB->next;
    }
}
void print(LinkedList L)
{
    LNode *p = L->next;
    bool flag = false;
    while (p)
    {
        if (p->xishu == 0)
        {
            p = p->next;
            continue;
        }
        printf("%d %d ", p->xishu, p->zhishu);
        flag = true;
        p = p->next;
    }
    if (!flag)
        printf("0\n");
}
void InitList(LinkedList &L, int index[], int len)
{
    L = (LinkedList)malloc(sizeof(LNode));
    L->next = nullptr;
    LNode *p;
    LNode *q = L;
    for (int i = 0; i < len; i += 2)
    {
        p = (LNode *)malloc(sizeof(LNode));
        p->xishu = index[i];
        p->zhishu = index[i + 1];
        p->next = nullptr;
        q->next = p;
        q = p;
    }
}
/**
 * 输入：2 7 3 5 12 1 6 0 -1 -1
 *       7 5 9 4 3 0 -1 -1
 * 输出：2 7 10 5 9 4 12 1 9 0
 *
 * */
int main()
{
    int i1 = 0, i2 = 0;
    int item = 0;
    int index1[200000];
    int index2[200000];
    while (item != -1)
    {
        scanf("%d", &item);
        index1[i1++] = item;
    }
    scanf("%d", &item);
    item = 0;
    while (item != -1)
    {
        scanf("%d", &item);
        index2[i2++] = item;
    }
    LinkedList L1;
    LinkedList L2;
    InitList(L1, index1, i1 - 1);
    InitList(L2, index2, i2 - 1);
    PolySum(L1, L2);
    print(L1);
}