位运算总结

运算符

位运算就是对整数在内存中的二进制位进行操作

操作数以二进制补码形式按位参与运算，且操作数只能是整型或字符型，不能是实型

不同长度的数据进行位运算时,如a&b,a–long,b–Int

• 右端对齐
• b是正数，则左侧16位补0
• b是负数，则左侧16位补1
• b是无符号整数，则左侧补0

与&–全1才1	或|–有1就1	异或^–相同为0	移位
0&0=0	0|0=0	0^0=0	左移一位==乘2（右边位补0）
0&1=0	0|1=1	0^1=1	正数右移一位==除2
1&1=1	1|1=1	1^1=0	负数>>1==除2 负数>>>1就变成正数
对某些位清0	对某些位置1	a^ a=0，a^ 0=a

取反

(-1)₁₀=(1111 1111)₂

~(-1)=(0000 0000)₂=(0)₁₀

~(127)=(1000 0000)₂=(-128)₁₀

右移

右移运算>>：右移后左边位补原最左位值(正数补0，负数补1)

右移运算>>>：右移后左边位补 0

取一个数的指定位

1&0=0

1&1=1

所以和1进行&运算，就可以得到这个位对应的数

如a=1010 1101，要取其低4位，则

a & 0000 1111

== 0000 1101

位翻转

1^0=1

1^1=0

所以和1进行异或，可以实现位翻转，如

a 1010 1101

^ 0000 1111

= 1010 0010

实现加法

二进制的运算规则

• 0+0=0
• 0+1=1
• 1+1=0，进位

比对运算符，可知只有异或的结果与之相同，但异或没有实现进位

而两者相与的结果就显示了要进位的位置，故a&b后左移一位，再和a^b相加，就是两个整数之和

实现代码为：

int add(int a,int b)
{
    int k1=a^b;
    int k2=a&b;
    k2=k2<<1;
    
    if(k2==0)   //无需进位
        return k1;
    else       //需进位
        return add(k1,k2);
}

由于int大小为32位，而k位的二进制相加，最多k次进位，所以最高执行32次

时间复杂度O(1)

实现乘除法、幂

int a = 2;
a >> 1;   //---> 1    右移÷2
a << 1;   //---> 4    左移*2
 
a>>k;     //a÷2^k
a<<k;     //a*2^k

1<<0=1;
1<<30=2^30;
1<<31=-2^31;

判断奇偶

二进制的表示中，奇数的最低位是1，偶数的最低位是0，而1的二进制是0000 0001，所以和1进行&运算，结果为1，就是奇数

//判断是否是奇数
bool is_odd(int n)
 {
 	return (n & 1 == 1);
    //等价于n%2==1
 }

交换两个数

异或是不同则1，同则0，所以a^a=0

又0^a=a

所以异或同一个数偶数次，则本身的值不变，如

• a^ B^ B=a
• x^ Y^ Y^ Y^Y=x

那么利用这个原理，可以实现两个数交换

要令a=b，则a=b^ a ^ a

要令b=a，则b=a^ b ^ b

故交换两个数的实现代码为：

void swap(int& a,int& b)
{
    a=a^b;
    b=a^b;
    a=a^b;
}

统计二进制中1的个数

解法一

假设n的二进制有k位，k≥0，则最直接的方法就是一位一位的检查是否为1，然后计数

又位运算&中，全1才1，也就是说，通过&，可以检查是否为1

要保证每次检查时，都只是检查第K位是不是1，那就得利用2的幂了

2的幂的二进制如下：

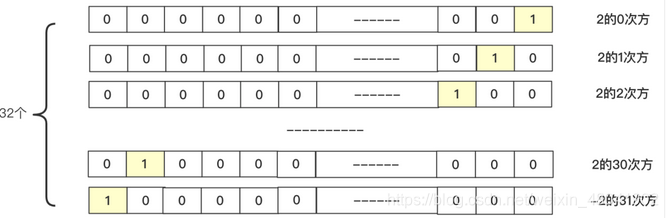
由图可知，把n的二进制中第k位与2^k进行与运算，如果结果不为0，说明第k位是1

且2^k=2^k-1<<1

实现代码为：

int number_of_1(int n)
{
    int count=0;
    for(int i=0;i<32;i++)
    {
        if((n&(1<<i))!=0)
            count++;
    }
    return count;
}

时间复杂度O(1)

解法二

如果n≠0，则n-1是（n）₂中最低位的1变成0，后面全为1，前面不变

如

n	0111	1011
n-1	0110	1010

假设（n）₂中最低位的1是第K位，则n-1的0-（k-1）位是n的0-（k-1）位取反

又a&a=a，所以n & (n-1) 相当于把n最后一个1变成0，如

n 101011000

n-1 101010111

& 101010000

不断进行此操作，直到&的结果为0，则&的次数就是1的个数

实现代码为：

int number_of_1(int n)
{
    int count=0;
    while(n!=0)
    {
        n=n&(n-1);
        count++;
    }
    count++;
}

时间复杂度O(1)

lowbit运算

定义一个函数f=lowbit(x)，这个函数的值是x的二进制表达式中最低位的1所对应的值

实现方法

• x&(x^(x-1))
• x&-x

参考：

https://mp.weixin.qq.com/s/JIUG2PIwNK_ebzCTeeyYlQ