梯度下降法几个注意点

1. 梯度下降法中是同时更新的θ0和θ1：
   同时更新θ0和θ1与不同时更新的区别如下：
   同时更新是最自然的方法。
   如图所示，如果同时更新与不同时更新两者是有区别的，同时更新时，两者都是在初始值得到的J的基础上进行更新；当不同时更新时，先在初始值θ0和θ1的基础上更新了θ0，再更新θ1时，此时是在新的θ0的基础上计算了J更新的θ1。
   θ0和θ1不同时变化如图左，θ0和θ1同时变化如图右
   
2. 梯度下降法中更新公式的导数项含义：
   如下图所示，假设只有一个参数θ1，若此时的θ1在J的最小值的右边（如下图中的上面的图），则若更新θ1，需要减去一个正数；若此时的θ1在J的最小值的左边（如下图中的下面的图），则若更新θ1，需要减去一个负数，而导数的表达式正好同时满足这两个条件。
   
3. 更新规则中的学习率α：
   学习率α过小或过大的影响如下图：
4. 在接近局部最优解时，更新的步长会逐渐变小：
   当接近全局最优解时，更新的步长会逐渐变小，这是因为当距离最优解越近时，导数项会逐渐变小，因此，也不需要随着时间改变α。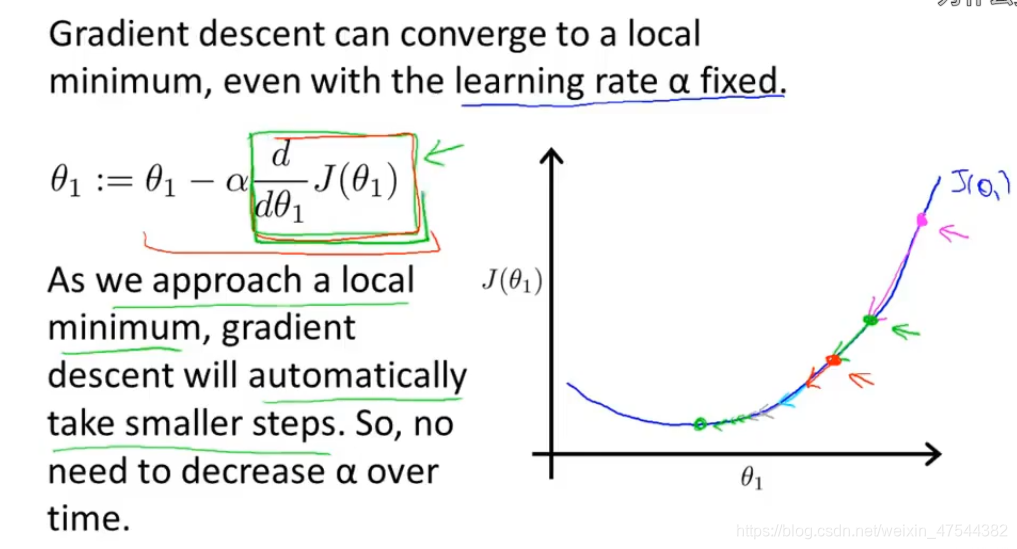
   注：图片来源于吴恩达老师讲解的机器学习视频。