题目描述:
环形公交路线上有 n 个站,按次序从 0 到 n - 1 进行编号。我们已知每一对相邻公交站之间的距离,distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
示例1:
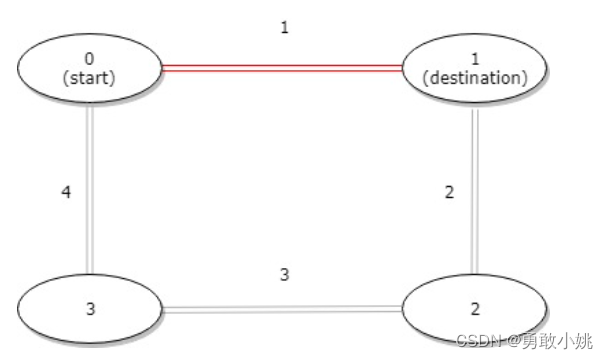
输入:distance = [1,2,3,4], start = 0, destination = 1
输出:1
解释:公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。
示例2:
输入:distance = [1,2,3,4], start = 0, destination = 2
输出:3
解释:公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。
解法一:迭代
思路:
Step1:用sum统计总的距离长度
Step2:用len统计由起始公交站到终点公交站之间的距离。假设len为顺时针的走法,那么sum-len的值即为逆时针的走法。
Step3:计算得到最小值即可。
代码:
class Solution {
public int distanceBetweenBusStops(int[] distance, int start, int destination) {
//统计距离总长
int sum = 0;
for(int n : distance){
sum += n;
}
//保证start比destination小
int len = 0;
if(start > destination){
int temp = start;
start = destination;
destination = temp;
}
//找到从start到destination之间的距离,假设这个len就是顺时针走的,那么sum-len后的距离就是逆时针走的,然后求最小值即可
for(int i=start; i < destination; i++){
len += distance[i];
}
return Math.min(len, sum-len);
}
}
解法二:
思路:
思路与解法一大同小异,不再赘述。
代码:
class Solution {
public int distanceBetweenBusStops(int[] distance, int start, int destination) {
int total = 0, s = 0, min = Math.min(start, destination), max = Math.max(start, destination);
for (int i = 0; i < distance.length; i++) {
total += distance[i];
if (min <= i && i < max) {
s += distance[i];
}
}
return Math.min(s, total - s);
}
}








 这篇博客介绍了如何解决环形公交路线上寻找最短路径的问题。提供了两种解法,分别是迭代和优化的方法,通过计算总距离和特定路径距离来确定乘客从起点到终点的最短行驶距离。
这篇博客介绍了如何解决环形公交路线上寻找最短路径的问题。提供了两种解法,分别是迭代和优化的方法,通过计算总距离和特定路径距离来确定乘客从起点到终点的最短行驶距离。

















 235
235

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








