REFT:基于强化微调的推理

概述

将FT和RL结合，使用RL负反馈提高微调效果。

SFT过程在训练数据上迭代了几个周期。所提出的ReFT从SFT预热并在相同数据上进行RL训练。

介绍

最先进的解决数学问题的方法采用了监督微调 （SFT）来使用思维链（CoT）注释训练模型。

通常，训练数据中的每个问题都有一个CoT注 释，即一条正确的推理路径，这在SFT中被利 用。我们观察到，这可能导致SFT模型的泛化能 力相对较弱。对于同一个问题，往往存在多个 有效的CoT注释，这强调了需要一种更强大的微调 方法。为了解决这个问题，我们提出了一种简 单但有效的方法，称为强化微调（Reinforced Fine-Tuning, ReFT）。

 SFT与ReFT在存在CoT替代方案时的比较

 

通过使用在线强化学习（RL）算法，特别是本论文中采用的近端策 略优化（PPO），模型 得以实现。以此方式，ReFT能够采样多条正确 的推理路径或CoT注释，并从中学习。

由于训练数据包含真实答案，因此在训练PPO 时，可以从这些数据中自然地推导出黄金奖 励。因此，不需要一个单独训练的奖励模型。 相比之下，RLHF必须 利用从人类标注数据中学习到的奖励模型。

在预热阶段，ReFT通过监督学习达到一定的准 确度。在强化学习阶段，ReFT通过采样各种 CoT推理路径进一步增强其能力。这样，ReFT 比SFT获得更丰富的监督信号。这种方法使得 ReFT在数学问题解决中大大提高了泛化能力。值 得注意的是，ReFT在使用相同训练题目的情况 下，优于SFT，且不依赖于额外的或增强的训练 题目。实际上，ReFT与这种数据工程并不冲 突，可以与之无缝结合。

主要贡献

• 提出了一种新颖的微调方法，即强化微 调（ReFT），该方法利用强化学习来解决数学 问题。与在相同数据集上进行传统监督微调相 比，ReFT展现了更强的泛化能力。

• 我们使用两个基础模型CodeLLAMA和Galactica在三个标准数据集上进行了广泛的实验： GSM8K、 MathQA和SVAMP。我们的实验涵盖了自然语言和基于程序的CoTs，展示了ReFT在性能和泛化 能力上的显著提升。

• 此外，我们展示了ReFT在推理时通过多数投 票和奖励模型重排序获得了优势，进一步提升 了其性能。

Method

在这项工作中，我们专注于自然语言链式推理 （N-CoT）和基于程 序的链式推理（P-CoT）使用 Python。Gao等提出了用于数学问题 解决的基于程序的链式推理。我们可以简单地执 行程序以获得答案。为了确保清晰并避免歧义， 我们分别使用术语N-CoT和P-CoT来表示自然语 言和基于程序的链式推理。

强化微调

提出的强化微调（ReFT）过程包括两个阶段： 预热阶段和强化学习阶段。总体算法如算法1所 示。

预热阶段在此阶段，政策在包含“(问题, 思维 链)”元组的数据集上进行几轮微调：(x, e)。这 使得模型具备基本的问题解决能力，从而生成 适当的响应。形式上，思维链生成过程可以分 解为一系列下一个标记预测动作。最后一个动 作标记表示生成过程的终止。思维链e表示为：

其中，L 代表最大长度。在时间步 t，动作 at 是从策略 πθ(·|st) 中采样的，其中 at 可以是词 汇表中的任意一个词，状态 st 包含问题中的所 有词以及到目前为止生成的所有词。每次动作 后，结果状态 st+1 是当前状态 st 和动作 at 的 连接： 

 

由于生成的动作为标记，因此产生的状态生成过程已完成。通过这种表示法， 样本的损失函数可以写为： 

 

 

强化学习

在这一阶段，策略通过一种在线自学习的方式来 提升其性能，使用的是由（问题，答案）元组组 成的训练数据集：(x, y)。具体来说，策略模型 通过反复采样响应，评估响应的答案正 确性，并以在线方式更新其参数。我们采用PPO与剪裁目标算法进行训练。按照Ziegler 等人的方法，值模型Vϕ是通过在策略 模型πθ的最后隐藏状态上添加一个线性值头构 建的，该策略模型πθ是在预热阶段之后得到 的。对于所有导致非终止状态的动作，奖励为 0。在终止状态下，我们使用一个奖励函数，该 函数直接比较从状态的CoT中提取的答案与真实 答案y。如果答案被认为是正确的，奖励函数返 回1，否则返回0。在答案均为数值的数据集 上，当可以提取答案且其为数值类型时，可以应 用部分奖励，奖励值为0.1。对于1 ≤ t ≤ L，我们 记为

 

这种部分奖励有助于减少从稀疏奖励中学习的影响。此外，我们的总奖励是奖励函数得分与学习到的 RL 策略和初始策略之间的 KullbackLeibler（KL）散度之和，该散度通过系数因子 β 进行缩 放。 

 

广义优势估计用于优 势计算：

 

 其中，时间差分（TD）定义为

 

其中，终端状态值 Vϕ(sL+1) := 0，λ ∈ (0, 1] 是奖励的折扣因 子，γ ∈ [0, 1] 是TD的折扣因子。对于回报的估计，我们利用了λ回报 ˆRt，它可以写成广义优势估计和价值估计的和：

 

最后，政策和价值目标可以写成如下两个方程 式：

 

其中，πθold 和 Vϕold 用于采样CoT并计算 ˆAt，ˆRt。统一的损失函数是上述目标的加权 和。

 

其中，α 是价值目标的系数。

Experiments

Datasets

我们对三个数学问题数据集进行了实验： GSM8K、SVAMP和 MathQA。 对于 GSM8K 和 SVAMP，答案的格式是一个数 值。在 MathQA 中，格式则是一个多选列表 （即 ABCD）。我们使用 GPT-3.5-turbo 进行少样本提示 以获得 NCoT 和 P-CoT 。我们还在 MathQA 的数值版本上进 行了额外的实验，其中格式也是一个数值。这 些实验用于展示我们在 MathQA 上对潜在奖励 操纵现象的假设 。

Baseline

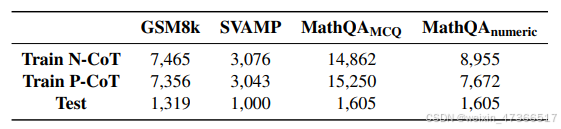
训练和测试数据集的统计信息。 

我们对比了ReFT与SFT和自训练基线方法。SFT简单 地在训练数据上微调语言模型。通过自我训练方法的实验确保了相 对公平的比较，因为这些方法共享一个机制， 即从模型生成的样本用于训练。

我们实现了离线自训练（Offline-ST）和在线自训练（Online-ST）。离线自训练方法类似于专家迭代 。我们首先使用早期检查 点中的SFT检查点来采样CoTs，并将其与标准 答案进行验证。我们仅保留那些答案正确的专 家样本。然后，我们对原始训练数据与这些专 家样本的组合进行SFT。

在线-ST方法被设计得与ReFT方法紧密可比。按 照ReFT的步骤，在线-ST也采用了相同的预热过 程。之后，我们进行持续训练，使用实时生成 的样本。在每个训练步骤中，模型首先为一批 样本采样CoTs，并仅保留那些答案正确的 CoTs。生成的批次既包含采样的CoTs，也包含 真实的CoTs。然后，我们使用监督微调目标 LSFT在这个批次上更新模型参数。与ReFT相 比，在线-ST既不使用带有错误答案的负面响 应，也没有专门的机制来防止模型显著偏离初 始模型，这可能导致任务特定的过拟合和训练 不稳定。

实验设置

我们使用两个基础模型进行实验： Galactica-6.7B5和 CodeLLAMA-7B67 。这 两个模型在数学求解方面表现出色，并在近期关 于推理任务的文献中被广泛采用。除了与基线进行比较外，我们还应用了常见的 技巧，即多数投票和奖 励模型重排序在 GSM8K上。

超参数

在所有实验中，训练使用8块A100-80GB GPU， 采用DeepSpeed的Zero Stage 2和 HuggingFace Accelerate。在ReFT的预热阶段，我们使用 AdamW优化 器，预热比例为10%。批量大小为48，学习率 为1e-5。最大长度设置为1024。预热阶段中的 轮数在所有设置中为2，除了在MathQAMCQ和 MathQAnumeric上分别使用最多5轮和10轮。 模型训练300轮，学习率为3e-7。根据Ziegler等 ，PPO中的λ、γ、α、ϵ和U分别设置 为1、0.95、5、0.2和2。KL系数β在P-CoT中设 置为0.01，在N-CoT实验中设置为0.05。关于 ReFT的更多超参数设置可以在附录B中找到。

对于SFT基线，我们训练模型40个周期，并选择 性能最佳的检查点。这个周期数已选择得足够 大，以确保SFT收敛。对于Offline-ST基线，我 们使用ReFT预热阶段的检查点来采样CoTs。使 用生成温度1.0和最大长度1024，我们为每个问 题采样100个CoTs，并仅保留那些答案正确 的。按照Singh等人的方法，我们将 CoTs子采样为每个问题10个随机唯一的CoTs， 以平衡问题的难度。微调周期的数量设置为 20，这足够大以确保训练收敛。如上所述， Online-ST基线试图模仿ReFT中的相同设置。我 们拥有相同的预热过程，超参数设置与ReFT大 致相同。

奖励模型重排序，我们训练了一个奖励模型 （RM）来判断CoT的正确性。为了构建RM训练 数据，我们使用预热阶段的模型，并对训练集 中的每个问题进行采样，以获得100个CoT。这 些CoT经过去重处理，并通过将提取的答案与标 准答案进行比较来获得二进制标签。作为一种常见做法，奖励模型是 从最佳SFT检查点初始化的语言模型。与基于结果的 奖励模型（ORM）类似， 奖励模型被训练来预测一个二元标签，指示“正 确”或“错误”的解决方案。一旦输入通过奖励模 型，分类操作会在最后一个标记的隐藏状态上 使用线性分类器进行。最后，在候选方案中， 具有最高“正确”分数的解决方案被选为最终答 案。我们使用批量大小为24、最大长度为700、 线性学习率调度（10%的预热期和最大学习率 为1e−6）对RM模型进行了3个epoch的训练。

我们报告了N-CoT和P-CoT在所有数据集上的值 准确性。对于多数投票和重排序，我们 采样了100个CoTs进行评估。在投票中，选择 具有多数计数的有效答案作为最终答案来计算 准确性。在重排序中，我们选择得分最高的CoT 并提取答案。

表2，ReFT与基于两个基础模型微调的基线在所有数据集上的价值准确性

Results

ReFT 在性能上超越了 SFT， 表2对比了在GSM8K、SVAMP和MathQA数据 集上，基线模型与提出的ReFT的表现。我们可 以观察到，除了在MathQAMCQ N-CoT上， ReFT在其他所有情况下都持续表现出比SFT更 好的性能。具体来说，我们在GSM8K N-CoT和 P-CoT上，分别使用CodeLLAMA对SFT实现了 接近10点和12点的改进。平均而言，我们在所 有数据集的N-CoT和P-CoT上，分别使用 CodeLLAMA实现了6.7点和7.4点的改进。值得 注意的是，ReFT中没有使用额外的注释或奖励 模型。这些强大的结果展示了ReFT的稳健泛化 能力，并展示了进一步探索训练数据与强化学习 的巨大潜力。

Math QAMCQ预测示例揭示了奖励破解。

离线自训练包括从初始策略中采样数据以进行 微调。我们可以看到，这种简单的基线方法相 比SFT能 提升性能，但提升幅度远不及ReFT所带来的改 进。这些比较表明，在ReFT中“探索”是实现良 好性能的关键。尽管在线自训练通过Galactica 实现了一些额外的改进，但平均而言，它仍然 远不及ReFT。这一结果表明，错误的实例对于 指导模型进行更好的探索也非常重要。与自训 练的比较还表明，提出的基于策略采样和强化 学习的方法优于标准的增强数据方法。

数学问答的奖励破解我们的研究调查了Math QA 多选题的负面结果，表明ReFT在训练过程中对多选题遭受了奖励作 弊。图3展示了采样的解决 方案如何产生“不准确奖励”，这使得RL训练受 到影响。如图所示，采样的CoT得到了一个错误 答案“172”，这并不是“18”和“22”乘积的一半。 然而，最终的推理步骤仍然预测选项“C”为最终 答案，因为模型总是会从{A, B, C, D, E}中预测 一个选项，而不考虑中间CoT8的正确性。因 此，这种误导性的CoT将获得一个正奖励“1”， 并误导模型将其视为正确的CoT。这种潜在的奖 励作弊现象严重影响了模型训练。这也是我们选择带有更长预热步骤的 检查点用于Math QA N-CoT以减少奖励作弊效应 的原因。

为了进一步展示多项选择题（MCQ）问题的负 面影响，我们对Jie和Lu提出的 MathQA变体——MathQAnumeric进 行了实验，该变体去除了问题中的选项，并直 接预测数值答案。表3展示了与基线方法的对比 结果。我们可以观察到，使用Galactica和 CodeLLAMA时，ReFT始终优于基线方法。理想 情况下，如果我们能够获得更细粒度的奖励，就可以减少MathQAMCQ中的奖励 操纵效应。然而，开发一个可靠的基于过程的奖励模型成本高昂，并且需要对推 理步骤进行大量手动标注。认识到这些挑战， 我们将控制奖励作弊及其分析视为未来工作中 需要解决的重要问题。

多数投票与重排序对ReFT的增益

我 们也采用了多数投票和奖励模型重排序的方 法，以展示ReFT能够从这些常见技术中受益。 具体而言，我们从SFT和ReFT策略中进行采 样。每道题目我们采样100个CoT解决方案，并 使用上述奖励模型进行重排序。表4的 结果显示，通过奖励模型重排序，ReFT在 GSM8K上始终表现最佳。ReFT + 投票在所有 设置中平均比SFT + 投票高出8.6分。采用重排 序的ReFT比采用重排序的SFT高出3分以上。

与现有的开源方法相比，我 们最好的P-CoT变体在GSM8K上达到了最佳性 能，准确率为81.2。此外，这些方法主要包括 从ChatGPT生成的额外数据，并在微调过程中 进行蒸馏。相比之下，我们通过挖掘现有训练 数据的潜力并推动策略性能的极限，直接改进 了策略本身。我们在表4中报告的最佳结果，即 CodeLLAMA + ReFT + Reranking与P-CoT设 置，甚至超过了GPT-3.5-turbo。然而，我们是 在仅有7B大小的模型上获得了这一结果。

表4，GSM8K上SFT和ReFT的多数投票和奖励模型重新排序的解决准确性。我们还包含了现有方法以供比较。

使用一个小型语言模型。我们在P-CoT数据上进 行了实验，使用了Galactica-125M、 Codeparrot-small 和Codegen-350M。令人惊讶 的是，ReFT在三个数据集上仍然优于SFT。这 些改进展示了ReFT在探索合理程序时的鲁棒 性。

消融研究

我们使用CodeLLAMA在GSM8K P-CoT 上进行消融研究（表6）。 在没有部分奖励的情况下，ReFT的准确性较 低，为74.4，但仍远优于SFT。 这种部分奖励有助于减少训练 过程中稀疏奖励的影响。 此外，如果我们将KL系数β设为0，策略分布很 容易崩溃并产生意外结果（即0准确性）。 对策略探索的空间施加约束显然是至关重要的 。 初始的预热步骤本质上加强了这些约束，并允 许策略在β所规定的范围内进一步探索。 我们还尝试了单独的价值模型，其中躯干参 数与策略模型初始化相同。 我们发现，这种设置使得策略在早期RL训练中 更快收敛，但最终达到了相当的性能。 与共享价值模型的原始设置相比，它的计算量 是两倍，然而， 由于一次额外的正向传播，带来了计算开销， 以及由于存储单独的价值网络而导致的内存成 本增加一倍。

Analysis

SFT在接近40th轮 次时收敛并开始过拟合。然而，我们可以看到在 40th轮次时，ReFT策略的平均奖励保持在80%到 90%之间，并且值的准确率也在不断提高。此 外，我们可以看到KL散度在开始时非 常大，然后保持在0到10之间的合理值。稳定的 KL散度表明我们的策略在一个包含适当程序的空 间内进行探索。底层的强化学习机制极大地提高 了ReFT的泛化能力。

定性评估

我们进行了一项人类评估，以定性地评估SFT模 型、Warmup检查点和ReFT模型的输出。评估 使用了50个问题，并从GSM8K测试集中抽取了 所有三个模型都能正确解决的解决方案样本。 我们请四位不同的注释者根据以下标准对推理 路径进行评分，每个标准评分范围为0到1。 使用一个小型语言模型。我们在P-CoT数据上进 行了实验，使用了Galactica-125M、 Codeparrot-small 和Codegen-350M。令人惊讶 的是，ReFT在三个数据集上仍然优于SFT。

这 些改进展示了ReFT在探索合理程序时的鲁棒 性。

• 逻辑：评估导致答案的逻辑是否正确。
• 命名：评估变量是否传达了适当且合理的语 义。
• 紧凑性：评估推理路径是否包含冗余信息。

为确保 评估的公正性和准确性，我们严格遵循以下设 置：(1) 每条推理路径的来源（来自SFT、 Warmup或ReFT）被匿名化，以防止标注者偏 见。(2) 四位不同的标注者负责不同部分的样 本。

尽管总体得分相当接近，ReFT的 表现略优于SFT，并且优于Warmup变体。需要 注意的是，SFT本质上是通过学习真实数据进行 训练的，因此其得分可能较高。这一比较分析 突显了ReFT在生成准确且语义连贯的推理路径 方面的稳健性。

ReFT何时超越SFT？

为了进一步研究ReFT与 SFT之间的关系，我们对不同预热步数的SFT进 行了ReFT训练。具体来说，如果预热步数为 3，这意味着策略从3 rd轮次的SFT检查点初始 化。我们可以看到，所有ReFT策略的性能在预 热结束后立即下降，直到训练轮次达到约8轮。 这是因为共享值模型中的线性层是随机初始化 的，可能需要几个轮次来调整分布。从30th 轮 次开始，SFT收敛，而所有ReFT变体仍在改 进。我们还可以看到，所有变体都显著优于 SFT，并且没有任何特定ReFT变体表现出明显 优势。

Conclusion

我们已经介绍了强化微调（ReFT）作为一种新 的微调模型方法，用于解决数学问题。与SFT不 同，ReFT通过探索多个CoT注释来优化不可微 的目标，以寻找正确答案，而不是依赖单一的 注释。

通过在三个数据集上使用两个基础模型进行广 泛的实验，我们证明了ReFT在性能和泛化能力 方面优于SFT。此外，我们还展示了使用ReFT 训练的模型与多数投票 和奖励模型重排序等技术的兼容性。

此外，ReFT在数学问题解决方面相较于多个公 开的、开源的同规模模型展现出了更优越的性 能。这证明了ReFT方法的有效性和实际价值。

未来工作

我们首次尝试将强化学习，特别是PPO算法，应用于微调大型语言 模型（LLMs）以解决数学问题。我们未来的工 作包括利用离线强化学习技术，开发一种无需预 热的训练方法以提高训练效率和性能，从而缩 小与重排序方法的差距。此外，Lightman等指出，一个经过良好训练的过程奖励 模型（PRM）可以显著提升性能。因此，探索 在强化学习训练中实施基于过程的奖励是值得 的。最后，由于ReFT是一种多用途的方法，我 们计划将其应用于更多可以通过思维链（CoT） 形式化的推理任务中。

pdf论文翻译,pdf转word,图片转word：

免费论文翻译，PDF转word