数据结构与算法--树

一、树

树(Tree)是n(n>=0)个结点的有限集。当n=0时成为空树，在任意一棵非空树中:
一有且仅有一个特定的称为根(Root)的结点;
一当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、 ...、 Tm，其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。

注意点：

—n>0时，根结点是唯一的，坚决不可能存在多个根结点。
—m>0时，子树的个数是没有限制的，但它们互相是一定不会相交的。

刚才所有图片中，每一个圈圈我们就称为树的一个结点。结点拥有的子树数称为结点的度-
(Degree)，树的度取树内各结点的度的最大值。一度为0的结点称为叶结点(Leaf)或终端结点;
一度不为0的结点称为分支结点或非终端结点，除根结点外，分支结点也称为内部结点。

结点间的关系

结点的子树的根称为结点的孩子(Child)，相应的，该结点称为孩子的双亲(Parent)，同一双亲的孩子之间互称为兄弟(Sibling)。

结点的祖先是从根到该结点所经分支上的所有结点。

结点的层次

结点的层次(Level)从根开始定一起,根为第一层，根的孩子为第二层。
其双亲在同一层的结点互为堂兄弟。
树中结点的最大层次称为树的深度(Depth)或高度。

如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。
森林(Forest)是m(m>=0)棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。

二、树存储结构

要存储树，简单的顺序存储结构和链式存储结构是不能滴!不过如果充分利用它们各自的特点，完全可以间接地来实现。

这里要介绍三种不同的表示法:双亲表示法、孩子表示法、孩子兄弟表示法。

双亲表示法

双亲表示法，言外之意就是以双亲作为索引的关键词的一种存储方式。
我们假设以一组连续空间存储树的结点，同时在每个结点中，附设一个指示其双亲结点在数组中位置的元素。
也就是说，每个结点除了知道自己是谁之外，还知道它的粑粑妈妈在哪里。

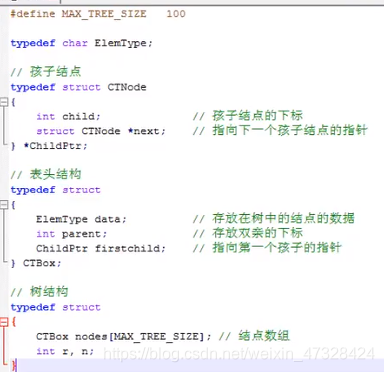
 孩子表示法

我们这次换个角度来考虑，由于树中每个结点可能有多棵子树，可以考虑用多重链表来实现。

 

KMP算法是三位老前辈（D.E.Knuth、J.H.Morris 和V.R.Pratt）的研究结果，大大的避免重复遍历的情况,全称叫做克努特-莫里斯-普拉特算法，简称KMP算法。