leetcode 785. 判断二分图

leetcode 785. 判断二分图

题目链接

https://leetcode.cn/problems/is-graph-bipartite/

问题描述

测试数据

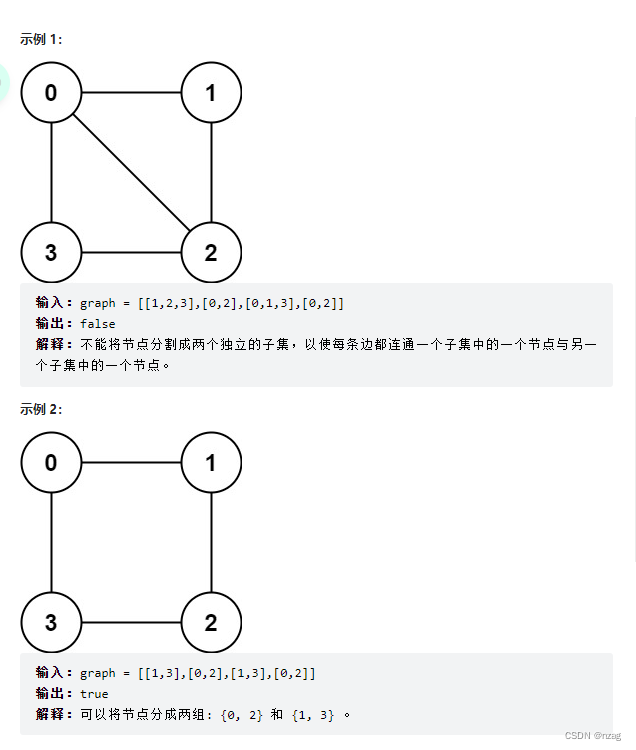
思路

在讲述思路之前，首先要了解一下什么是二分图。官方的定义我在此不做赘述了，简单来说，二分图的定义就是由一条边相连的两个顶点不出现在一个集合里，当通过这个条件将所有的顶点均分为两个集合时，即满足二分图的要求。常规的解法有并查集和dfs，bfs我不习惯，所以就不写了，感兴趣的可以自己研究。

首先说并查集，并查集是求连通分量类问题一个很简单易懂的方法。我们之前说过，连接顶点的两个边不能出现在一个集合，换句话说，与某个顶点通过临界边相连的其他顶点一定是在一个集合的，因此，我们可以通过并查集来进行合并。将与某个顶点的其他顶点连在一个连通分量，遍历所有顶点，当该顶点和与其连接的顶点在同一个连通分量，那么证明该图不能二分。

DFS的思路可以参考染色问题，相连顶点的颜色不同，则该图可以二分，否则该图不能二分。

具体实现

#并查集
class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        def find(x):
            if x != pre[x]:
                pre[x] = find(pre[x])
            return pre[x]
        def join(a,b):
            pa = find(a)
            pb = find(b)
            if pa != pb:
                pre[pa] = pb
        def isconnect(a,b):
            return find(a) == find(b)
        pre = [i for i in range(len(graph))]
        for i in range(len(graph)):
            for v in graph[i]:
                if not isconnect(i,v):
                    join(graph[i][0],v)
                else:
                    return False
        return True
 ___________________________________________________________________________________________________________________
 #DFS
 class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
    	n = len(graph)
        visit = [False] * n
        color = [False] * n
        flag = True
        def dfs(graph,v):
            nonlocal flag,visit,color
            visit[v] = True
            if not flag:
                return
            for adj in graph[v]:
                if not visit[adj]:
                    color[adj] = not color[v]
                    dfs(graph,adj)
                else:
                    if color[adj] == color[v]:
                        flag = False
        for i in range(n):
            dfs(graph,i)
        return flag
 ____________________________________________________________________________________________________________________________
 #还是补一下bfs吧 
 class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        n = len(graph)
        visit = [False] * n
        color = [False] * n
        flag = True
        def bfs(graph,v):
            nonlocal flag
            q = deque()
            q.append(v)
            visit[v] = True
            while len(q) > 0:
                node = q.popleft()
                for adj in graph[node]:
                    if not visit[adj]:
                        visit[adj] = True
                        color[adj] = not color[node]
                        q.append(adj)
                    else:
                        if color[adj] == color[node]:
                            flag = False
                            return
        for i in range(n):
            bfs(graph,i)
        return flag

总结

二分图的关键在于把握边的两边的两个结点不要在一个连通分量！！！！