吴恩达机器学习课后作业6——使用支持向量机(svm)构建一个垃圾邮件分类器

学吧，学无止境...

已于 2022-06-23 20:02:24 修改

阅读量2.8k

点赞数 3

文章标签：机器学习支持向量机 sklearn 人工智能算法

于 2022-06-23 20:01:58 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_46915208/article/details/125427559

版权

1. 问题和数据

在本练习中，您将使用支持向量机(svm)构建一个垃圾邮件分类器。

在本练习的前半部分，您将使用支持向量机(svm)处理各种示例2D数据集。使用这些数据集进行试验将帮助您直观地了解支持向量机的工作方式，以及如何在支持向量机中使用高斯核。
在练习的下一部分中，您将使用支持向量机构建一个垃圾邮件分类器

对于线性可分案例，我们的任务是找到一条最佳的决策边界，使得离这条决策边界最近的点到该决策边界的距离最远，即为要有最大间隔。

损失函数公式如下：
图片替换文本

在本节中要用到新的库，scikit-learn,简称sklearn。可以进行数据的预处理以及最后算法的评估。

2.线性可分案例

导入包，numpy和pandas是做运算的库，matplotlib是画图的库。
数据集是在MATLAB的格式，所以要加载它在Python，我们需要使用一个SciPy工具。
图片替换文本

import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt

导入数据集

data = sio.loadmat('ex6data1.mat')
print('data.keys():', data.keys())

输出结果：

data.keys(): dict_keys(['__header__', '__version__', '__globals__', 'X', 'y'])

指定X, y, 打印shape来看看

X, y = data['X'], data['y']
print('X.shape, y.shape:', X.shape, y.shape)
print('X:', X)
print('y:', y)

输出shape和X，y

X.shape, y.shape: (51, 2) (51, 1)
X: [[1.9643   4.5957  ]
 [2.2753   3.8589  ]
 [2.9781   4.5651  ]
 [2.932    3.5519  ]
 [3.5772   2.856   ]
 [4.015    3.1937  ]
 [3.3814   3.4291  ]
 [3.9113   4.1761  ]
 [2.7822   4.0431  ]
 [2.5518   4.6162  ]
 [3.3698   3.9101  ]
 [3.1048   3.0709  ]
 [1.9182   4.0534  ]
 [2.2638   4.3706  ]
 [2.6555   3.5008  ]
 [3.1855   4.2888  ]
 [3.6579   3.8692  ]
 [3.9113   3.4291  ]
 [3.6002   3.1221  ]
 [3.0357   3.3165  ]
 [1.5841   3.3575  ]
 [2.0103   3.2039  ]
 [1.9527   2.7843  ]
 [2.2753   2.7127  ]
 [2.3099   2.9584  ]
 [2.8283   2.6309  ]
 [3.0473   2.2931  ]
 [2.4827   2.0373  ]
 [2.5057   2.3853  ]
 [1.8721   2.0577  ]
 [2.0103   2.3546  ]
 [1.2269   2.3239  ]
 [1.8951   2.9174  ]
 [1.561    3.0709  ]
 [1.5495   2.6923  ]
 [1.6878   2.4057  ]
 [1.4919   2.0271  ]
 [0.962    2.682   ]
 [1.1693   2.9276  ]
 [0.8122   2.9992  ]
 [0.9735   3.3881  ]
 [1.25     3.1937  ]
 [1.3191   3.5109  ]
 [2.2292   2.201   ]
 [2.4482   2.6411  ]
 [2.7938   1.9656  ]
 [2.091    1.6177  ]
 [2.5403   2.8867  ]
 [0.9044   3.0198  ]
 [0.76615  2.5899  ]
 [0.086405 4.1045  ]]
y: [[1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [1]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [0]
 [1]]

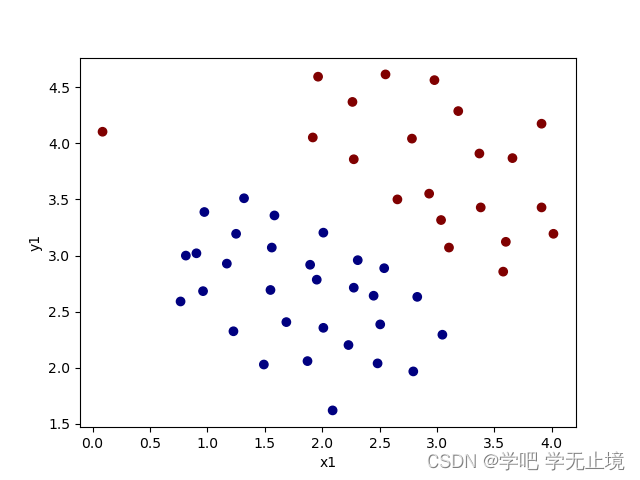
画出数据的散点图来看看分布状况

def plot_data():
    plt.scatter(X[:, 0], X[:, 1], c=y.flatten(), cmap='jet')  #　cmap相当于是配色盘的意思，这次选择了jet这一套颜色。y.flatten()
    # 是将y拉伸成一列， 这样每一个X对应一个y,而y只有0，1两种，c是给数据点颜色,把0和1的数据点给出不同的颜色
    plt.xlabel('x1')
    plt.ylabel('y1')
    plt.show()

plot_data()  # 调用函数，画出数据的散点图来看看分布状况

导入sklearn.svm，

from sklearn.svm import SVC

SVC的用法如下：

使用sklearn.svm的svc进行求解

svc1 = SVC(C=1, kernel='linear')  # C是误差惩罚系数，代替之前使用lamda的方式，用来调节模型方差与偏差的问题; kernel我们暂就用linear
svc1.fit(X, y.flatten())  # 此处默认跟着操作的，格式问题记住这样用就行
print(svc1)
print(svc1.predict(X)