简单线性代码表示-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_46886075/article/details/146065648

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

前言
一、数据处理
- 数据集生成
- 数据处理
二、模型构建
- 1.预测模型与损失函数
- 2.梯度回传
超参数设置与训练
总结

前言

提示：这里可以添加本文要记录的大概内容：

我们通过写一个在pycharm上写一个简单的线性回归，来理解神经网络的基本训练过程。我们假设，通过了解一个人的外貌，性格，财富，内涵，来推断他的恋爱次数，即将前四者视为X，恋爱次数视为Y，进行模拟推断。

提示：以下是本篇文章正文内容，下面案例可供参考

一、数据处理

数据集生成

先设置一个生成数据函数，参数为w权重，b偏置项，data_num生成的数量，通过使用pytorch的normal生成一个形状为（data_num，len（w））的张量x，每个元素是通过从均值为0、标准差为1的正态分布中随机采用获得。y = w*x+b，注意其中x，w，b均为矩阵。
同时，为了增强真实性，我们会设置一个与y同样形状的噪声向量，将噪声与y相加，用于模拟现实中的外部干扰。
选择X的某一列（即，选择某一变量，性格或财富等），使用matplotlib绘制出其与Y之间的关系的散点图。

import torch
import matplotlib.pyplot as plt                                 #  画图的
import random                                                   #随机

    #生成数据
def create_data(w, b, data_num):                #w为权重，b为偏置项，data_num表示要生成的数据点的数量

    # 使用 PyTorch 的 normal 函数生成一个形状为 (data_num, len(w)) 的张量 x，其中每个元素都是从均值为 0、标准差为 1 的正态分布中随机采样的。
    x = torch.normal(0, 1, (data_num, len(w)))
    y = torch.matmul(x, w) + b                  #matmul表示矩阵相乘

    # 这行代码生成一个与 y 形状相同的噪声向量，其中每个元素都是从均值为 0、标准差为 0.01 的正态分布中随机采样的。
    noise = torch.normal(0, 0.01, y.shape)      #噪声要加到y上
    y += noise

    return x, y

num = 500
true_w = torch.tensor([8.1,2,2,4])
true_b = torch.tensor(1.1)

#X为（500，4）的矩阵，Y为（500，1）的矩阵
X, Y = create_data(true_w, true_b, num)		##通过选取第四列，将X，Y的形式归一化

plt.scatter(X[:, 3], Y, 1)
plt.show()

数据处理

设计完生成函数后，我们对数据集的操作还没有结束，我们还需要一个数据提供函数，在后续模型训练过程中，可以将数据简单处理后直接提供给模型。
函数主要工作流程

生成索引列表并打乱顺序。
循环遍历数据集，每次提取一个批次的数据和标签。
使用 yield 返回当前批次的数据和标签，并保留函数状态。
下次调用时，继续从上次停止的地方执行，返回下一个批次的数据。

数据集方面处理完成后，我们进行后续模型方面的构造。

#每次访问这个函数， 就能提供一批数据
def data_provider(data, label, batchsize):       #data即为x，label即为y，batchsize为每一批数据的个数
    length = len(label)         #lable的长度即为样本数量

    #length为500，range(length)：为从0到499的范围
    indices = list(range(length))   #indices为一个从0到length-1的一个列表，或者说索引列表

    #我不能按顺序取，因为会影响程序的普适性和随机性，需要把数据打乱
    random.shuffle(indices)

    # 循环遍历数据集，每次跳过的步长为 batchsize
    for each in range(0, length, batchsize):
        get_indices = indices[each: each+batchsize] #从打乱的索引列表中获取当前批次的索引
        get_data = data[get_indices]
        get_label = label[get_indices]

        yield get_data,get_label  #有存档点的return

batchsize = 16

二、模型构建

1.预测模型与损失函数

模型构建方面中包括，模型预测，损失函数计算，以及梯度回传。其中预测与损失函数，由于我们是简单演示代码，所以设计的较为简单，分别是一个线性函数和预测值与真实值差的绝对值。

def fun(x, w, b):       #求预测值
    pred_y = torch.matmul(x, w) + b
    return pred_y

def maeLoss(pre_y, y):  #求损失函数loss
    return torch.sum(abs(pre_y-y))/len(y)

2.梯度回传

我们之前提到过，计算损失函数的目的是为了调整预测模型，让损失函数的值减小。而为了找到最适合的权重，我们使用梯度回传，即通过参数-参数的偏导*学习率的方式进行计算。
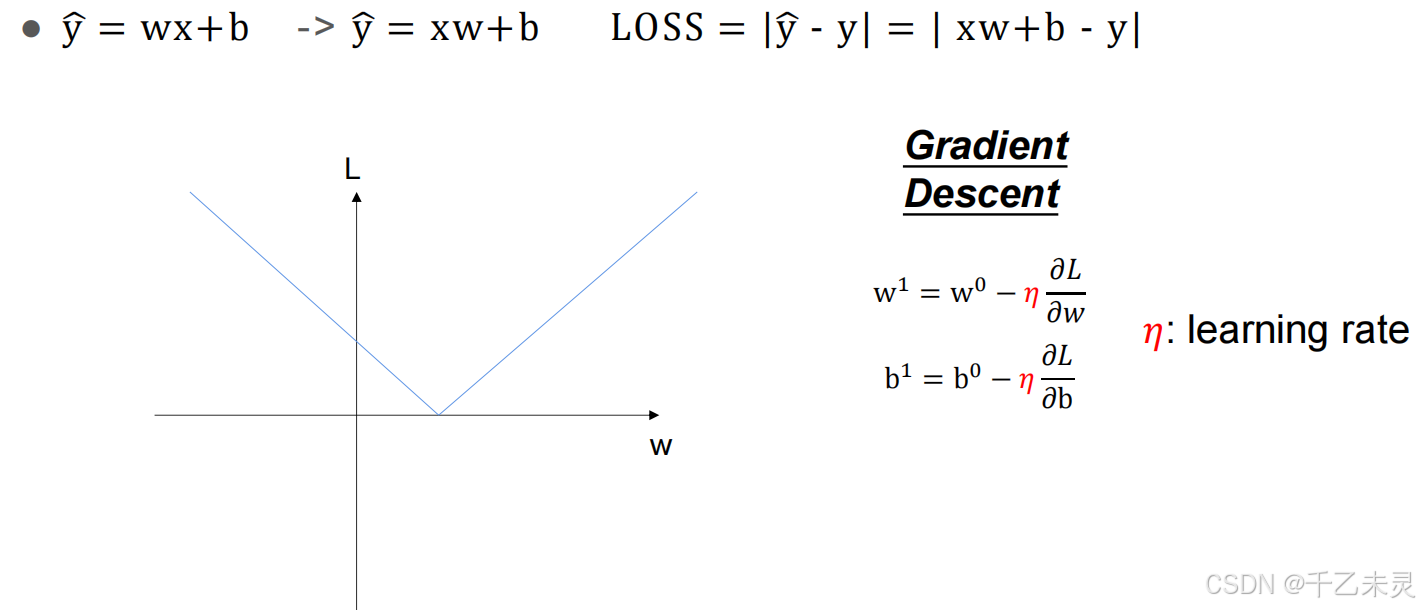
在这里插入图片描述

#paras（parameter）是一个包含模型参数的列表，lr:学习率（learning rate）
def sgd(paras, lr):          #梯度下降（Stochastic Gradient Descent, SGD）随机梯度下降，更新参数
    with torch.no_grad():  #属于这句代码的部分，不计算梯度
        for para in paras:
            para -= para.grad * lr      #不能写成   para = para - para.grad*lr
            para.grad.zero_()      #使用过的梯度，归0

在梯度回传的函数中，需要注意的是，在张量网上，我们的每一次计算都会积攒梯度。但并不是所有的梯度都是我们想要的，我们需要的是前向过程中产生的预测值，与真实值的偏差在回传中的梯度。这种梯度才能有效帮助我们减小loss。但回传过程中，我们依然会产生梯度，影响我们对真实所需值的判断，故需要使用with torch.no_grad()，停止梯度产生。
除此之外，在 PyTorch 中，梯度是累加的。每次调用 backward() 时，梯度会累加到 grad 属性中。在更新参数后，需要将梯度清零，否则下一次反向传播时梯度会继续累加，导致错误的结果。

#paras（parameter）是一个包含模型参数的列表，lr:学习率（learning rate）
def sgd(paras, lr):          #梯度下降（Stochastic Gradient Descent, SGD）随机梯度下降，更新参数
    with torch.no_grad():  #属于这句代码的部分，不计算梯度
        for para in paras:
            para -= para.grad * lr      #不能写成   para = para - para.grad*lr
            para.grad.zero_()      #zero_(): 是 PyTorch 中的原地操作（in-place operation），直接修改 grad 属性。使用过的梯度，归0

超参数设置与训练

设定好超参数（即需要预先手动设置的参数）后，我们开始了训练。过程中，我们使用了之前的函数，将数据提取，计算损失函数loss，以及优化梯度。除此之外，我们还使用了loss.backward() 函数，沿着计算图（computation graph）反向传播，计算每个参数的梯度。PyTorch 自动应用链式法则，计算损失对参数的梯度。梯度告诉参数应该向哪个方向调整才能减少损失（即“下山”的方向）。
同时，因为 Matplotlib 只能处理 NumPy 数组或 Python 原生数据类型，需要使用 .detach().numpy() 将 PyTorch 张量转换为 NumPy 数组，还可以确保不破坏计算图。

lr = 0.03
w_0 = torch.normal(0, 0.01, true_w.shape, requires_grad=True)   #这个w需要计算梯度
b_0 = torch.tensor(0.01, requires_grad=True)
print(w_0, b_0)

#训练循环次数
epochs = 50

for epoch in range(epochs):
    data_loss = 0
    for batch_x, batch_y in data_provider(X, Y, batchsize):
        pred_y = fun(batch_x,w_0, b_0)
        loss = maeLoss(pred_y, batch_y)
        loss.backward()         #反向传播，计算梯度。
        sgd([w_0, b_0], lr)
        data_loss += loss

    print("epoch %03d: loss: %.6f"%(epoch, data_loss))


print("真实的函数值是", true_w, true_b)
print("训练得到的参数值是", w_0, b_0)

idx = 3
plt.plot(X[:, idx].detach().numpy(), X[:, idx].detach().numpy()*w_0[idx].detach().numpy()+b_0.detach().numpy())
plt.scatter(X[:, idx], Y, 1)
plt.show()