数据结构（1）：树

简介

树这种数据结构在前端日常开发中是比较常见的，诸如经常接触的DOM树、级联选择、树形控件等等，都是利用树这种数据结构实现的。
在JS中一般是通过Object和Array这两家数据类型来构建树结构的。结构如下图

---

深度优先遍历

口诀：顾名思义就是尽可能深入的去搜索树的分支并且访问他们。用图看一下就比较好理解了。

算法实现：这个算法实现也比较简单，通过forEach去递归遍历子节点就可以了，代码如下

const tree = {
        val: 'a',
        children: [
            {
                val: 'b',
                children: [
                    {
                        val: 'd',
                        children: []
                    },
                    {
                        val: 'e',
                        children: []
                    }
                ]
            },
            {
                val: 'c',
                children: [
                    {
                        val: 'f',
                        children: []
                    },
                    {
                        val: 'g',
                        children: []
                    }
                ]
            }
        ]
    }

    const dfs = (root) => {
        console.log(root.val);
        root.children.forEach(dfs)
    }

    dfs(tree)

结果如下

---

广度优先遍历

口诀：先访问离根节点最近的节点，也可以理解成先访问完自己的子节点，再去访问子节点的子节点，概念图如下。

算法实现：主要思路就是通过一个队列，1.将根节点入队，2.把队头出队并且访问，3.最后把队头的子节点依次入队，重复 2、3点直到队列为空为止。

const tree = {
        val: 'a',
        children: [
            {
                val: 'b',
                children: [
                    {
                        val: 'd',
                        children: []
                    },
                    {
                        val: 'e',
                        children: []
                    }
                ]
            },
            {
                val: 'c',
                children: [
                    {
                        val: 'f',
                        children: []
                    },
                    {
                        val: 'g',
                        children: []
                    }
                ]
            }
        ]
    }

    const bfs = (root) => {
        const q = [root]  // 创建队列
        while (q.length > 0) {
            const n = q.shift()  // 队头出队
            console.log(n.val);  // 访问队头
            n.children.forEach(child => q.push(child))  // 遍历队头子节点并依次入队
        }
    }

    bfs(tree)

---

二叉树的先中后序遍历

二叉树概念：树中每个节点最多只能有两个子节点
JS中模拟二叉树可以通过Object来实现：

先序遍历

口诀：先访问根节点，再对根节点的左子树进行先序遍历，再对根节点的右子树进行先序遍历，简单来说就是 根 => 左 => 右 这么个顺序。遍历顺序如下

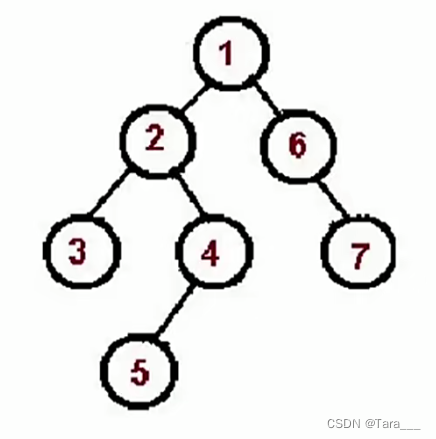
代码如下：

    const binaryTree = {
        val: 1,
        left: {
            val: 2,
            left: {
                val: 4,
                left: null,
                right: null
            },
            right: {
                val: 5,
                left: null,
                right: null
            }
        },
        right: {
            val: 3,
            left: {
                val: 6,
                left: null,
                right: null
            },
            right: {
                val: 7,
                left: null,
                right: null
            }
        }
    }

    const preOrder = (root) => {
        if (!root) return   // 拦截 null
        console.log(root.val);  // 访问根节点
        preOrder(root.left);  // 递归左子树
        preOrder(root.right);  // 递归右子树
    }

    preOrder(binaryTree)

结果如下

---

中序遍历

口诀：先访问根节点的左子树并对其进行中序遍历，再访问根节点，最后访问根节点的右子树并进行中序遍历，也就是 左子树 => 根 => 右子树
理解图如下：

代码如下：

    const binaryTree = {
        val: 1,
        left: {
            val: 2,
            left: {
                val: 4,
                left: null,
                right: null
            },
            right: {
                val: 5,
                left: null,
                right: null
            }
        },
        right: {
            val: 3,
            left: {
                val: 6,
                left: null,
                right: null
            },
            right: {
                val: 7,
                left: null,
                right: null
            }
        }
    }

    const inOrder = (root) => {
        if (!root) return   // 拦截 null
        inOrder(root.left);  // 递归左子树
        console.log(root.val);  // 访问根节点
        inOrder(root.right);  // 递归右子树
    }

    inOrder(binaryTree)

结果如下：

后序遍历

口诀：访问根节点左子树并进行后序遍历，再访问根节点右子树并进行后续遍历，最后访问根节点

代码：

    const binaryTree = {
        val: 1,
        left: {
            val: 2,
            left: {
                val: 4,
                left: null,
                right: null
            },
            right: {
                val: 5,
                left: null,
                right: null
            }
        },
        right: {
            val: 3,
            left: {
                val: 6,
                left: null,
                right: null
            },
            right: {
                val: 7,
                left: null,
                right: null
            }
        }
    }

    const postOrder = (root) => {
        if (!root) return   // 拦截 null
        postOrder(root.left);  // 递归左子树
        postOrder(root.right);  // 递归右子树
        console.log(root.val);  // 访问根节点
    }

    postOrder(binaryTree)

结果：

先中后序遍历 非递归版

（1）先序遍历
这里先将right入队，是因为我们用了数组的pop方法，拿到的是数组最后一个元素，先将right推入数组中再将left推入数组中，可以保证先将left出队并访问。

const preOrder = (root) => {
        if (!root) return   // 拦截 null
        let stack = [root]
        while (stack.length) {
            let n = stack.pop()
            console.log(n.val)
            if (n.right) stack.push(n.right)
            if (n.left) stack.push(n.left)
        }
    }

（2）中序遍历

    const inOrder = (root) => {
        if (!root) return   // 拦截 null
        let stack = []
        let p = root
        while (stack.length || p) {
            while(p) {
                stack.push(p)
                p = p.left
            }
            let n = stack.pop()
            console.log(n.val)
            p = n.right
        }
    }

（3）后序遍历
这里的思路就是通过两个数组来记录出队的顺序，stack数组用来遍历树的节点，按照 根 => 右 => 左的顺序将节点树推入 outputStack 数组中，这样一来在 outputStack 数组中就可以通过pop方法来实现 左 => 右 => 根 的后序遍历顺序了。

    const postOrder = (root) => {
        if (!root) return   // 拦截 null
        let stack = [root]
        let outputStack = []
        while (stack.length) {
            const n = stack.pop()
            outputStack.push(n)
            if (n.left) stack.push(n.left)
            if (n.right) stack.push(n.right)
        }
        while (outputStack.length) {
            const n = outputStack.pop()
            console.log(n.val)
        }
    }