电磁场与仿真软件(19)

Walt Lu

于 2022-09-15 19:08:50 发布

阅读量493

点赞数 1

文章标签：算法射频工程

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/weixin_46649493/article/details/126821918

版权

先补充下上一篇最后的结果的解释: $S^{(ref)},S^{(tm)}$ 修正

首先是 $S^{(ref)}$ ,如下图

红色区域代表的是入射介质

L->0是因为入射介质面是一个面,理论是就不应该存在厚度,

但我们因为方便计算, 做了2个近似

首先是layer1左边有个L->0的自由空间(无损耗,基本无相位差)

第二个近似是把入射介质也看成一个L->0的layer0,这样就可以直接之前的公式使用了.

代入如下公式,

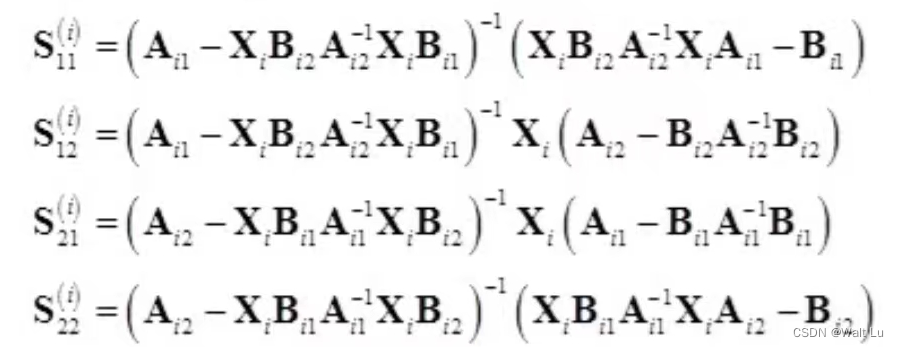
需要特别注意,这张图看的反射波,所以是从右往左看,所以自由空间的是1,介质层是2得到如下:

$X_{i}=1$ ；

$A_{i2}=W_{i}^{-1}W_{i}+V_{i}^{-1}V_{i}=2I; B_{i2}=W_{i}^{-1}W_{i}-V_{i}^{-1}V_{i}=0$ ；

$A_{i1}=A_{ref}=W_{i}^{-1}W_{0}+V_{i}^{-1}V_{0}; B_{i1}=B_{ref}=W_{i}^{-1}W_{0}-V_{i}^{-1}V_{0}$

然后计算,这边只计算S11,其他同理可求:

$S^{i}_{11}=(A_{ref}-0)^{-1}(0-B_{ref})=-A_{ref}^{-1}B_{ref}$ 和之前的结论是一样的;

再看Stm

$A_{i1}=W_{i}^{-1}W_{i}+V_{i}^{-1}V_{i}=2I; B_{i1}=W_{i}^{-1}W_{i}-V_{i}^{-1}V_{i}=0$ $A_{i1}=A_{tm}=W_{0}^{-1}W_{i}+V_{0}^{-1}V_{i}; B_{i1}=B_{tm}=W_{0}^{-1}W_{i}-V_{0}^{-1}V_{i}$ ;

得到:

$S_{11}=(2I-0)^{-1}(B_{tm}A_{tm}^{-1}2-0)=B_{tm}A_{tm}^{-1}$

我们比较下:

每个layer邻近都有一个长度 $L\rightarrow 0$ 自由空间的近似；

没有这个自由空间；

结果的比较,来看下这个近似的合理性:

先把近似计算的结果贴上去:

如果直接计算:

A的左边是自由空间,和模型是一样,右边是介质B,

先列出关系式如下:

计算比我想象的复杂多了，两边都要算到 $W_{A},W_{B},V_{A},V_{B},$ ..matlab正在看怎么算,算完后会再补充上传.

参考:Dr.Raymond Rumpf在youtube上的CEM课程

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

Walt Lu 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。