这篇是记录电磁场基本知识的最后一篇,后面将正式开始CEM部分
1. 色散
在写色散前,需要介绍下相速度和群速度:
假设有2列z方向的电磁波叠加,方便计算,两列波的频率分别为,两列波的波数分别为
这边有2项,第一项变化很慢的项,第二项是变化很快的项,先看第一项:
两边对时间取微分
称为群速度;
一样对时间t取微分
称为相速度;
群速度与相速度之前的关系:
可以得到:
我们比较关心项, 对于在材料中传播的电磁波,
-- 在真空中, 都是固定的,
所以
--在介电物质中传输的电磁波,介电常数是由里面的电偶极子决定的,介电常数往往是信号频率的函数,即 ,
也会是
的函数
, 所以
不会等于0
当 即高频信号的相速度比低频信号慢,可以得到
--正常色散;
当 即低频信号的相速度比高频信号慢,可以得到
--非正常色散;
色散图一般用的是曲线图
是波数(也就是我上面写的k,我一直没搞明白两者区别)
如下图:

材料中随
怎么变化很复杂, 在不同的频率区间有不同的变化,还没完全看明白.看明白后在后续章节再更新.
2. 偏振(极化)
偏振态通式分析:
假设有一列沿着z方向传播的电磁波,E在X,Y平面的大小和相位都不相同,我们可以用下列表达式表示这列电磁波:
,
如果,那么称为线性极化.
,这两个方程消除
得到下面式子:

这边需要用到一个数学公式去理解:
如果
,那么这个描述的是一个椭圆方程
上式 得到
这是个椭圆方程,如下图:
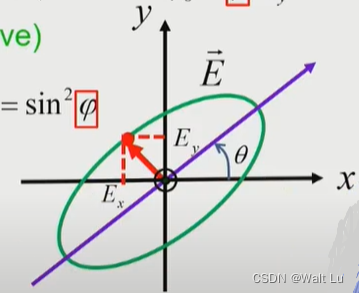

把,
用复数phasor形式写出
这个被称为Jones vectors.
考虑一些特殊值, , 带入

得到: 标准椭圆方程 如下,这个称为椭圆极化

Jones Vector :
如果 ,那么
得到: 圆方程, 这个称为圆极化:








 本文介绍了电磁场中的色散现象和偏振概念。色散分为正常色散和非正常色散,取决于高频和低频信号的相速度关系。在真空中相速度恒定,但在介电物质中,由于介电常数随频率变化,导致色散。同时,文章详细探讨了线性、椭圆和圆偏振的数学表示,并展示了椭圆偏振的图形解释。
本文介绍了电磁场中的色散现象和偏振概念。色散分为正常色散和非正常色散,取决于高频和低频信号的相速度关系。在真空中相速度恒定,但在介电物质中,由于介电常数随频率变化,导致色散。同时,文章详细探讨了线性、椭圆和圆偏振的数学表示,并展示了椭圆偏振的图形解释。

















 5076
5076

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










