最近公共祖先LCA倍增算法

LCA定义

LCA(Least Common Ancestors):最近公共祖先即两个结点最近的公共祖先

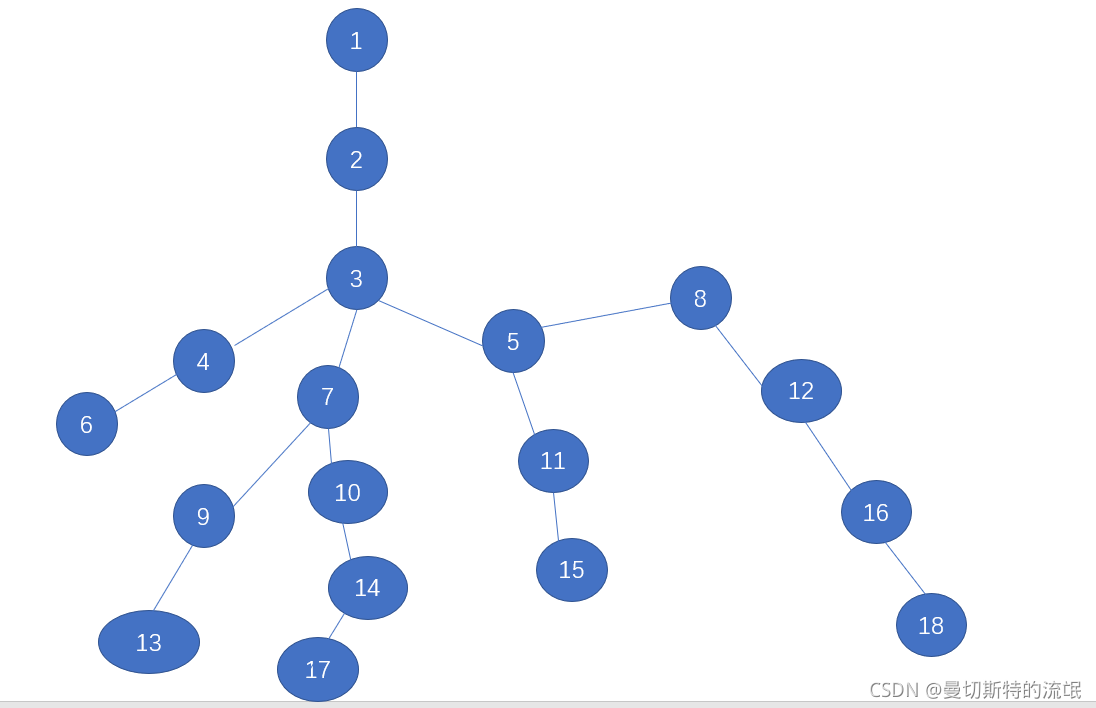
由上图可以看到 5号结点和7号结点的LCA为3号结点,9号结点和10号结点的LCA为7号结点。

一般算法

首先可以将两个结点统一到相同深度,然后一起向上一步一步走,直到他们踩到相同点,则该点为他们的LCA 。

(树的深度:与根节点的距离则为树的深度,根节点的深度为0或者1,根据个人喜好设置)

复杂度分析

因为每次向上走一步,最多n个结点深度最大也就为n,所以最多也就走n步,复杂度为O(n)

倍增算法

既然每次走一步太慢了,那么能不能快一点走呢?
每次走k步呢?

Sure当然可以But!

首先给出答案,每次走2的k次幂步 1、2、4、8、16…,那么有个问题我是从大步向小步走呢?还是小步向大步走呢?eg5=2^0+2 ^1+2 ^2-2 ^1 如果从小—>大走那么需要回退也就是减去2 ^1这个过程,那么从大向小走呢5= 2 ^2+2 ^1 可以完美解决回退这个问题!

通过上面分析,我们每次走2的k次幂步,并且k是依次递减的

有一个问题,每次走2的k次幂,那么我怎么知道图中从x结点走了2的k次幂步后的结点是哪一个呢???

通过预处理可以求出第i个结点 走了2^j步后的结点编号

倍增算法的核心

递推公式f(i,j)=f(f(i,j-1),j-1)
f(i,j)表示第i个结点走2^j步后的结点
那么也就是第f(i,j-1)这个结点向前走2^j-1步两者可以达到同一效果!
eg: 2^4=2 ^3+2 ^3=16
也就是我只要求出f(2,3)就可以递推求出f(2,4)

通过预处理后,我可以求得任意一点走2^k后的结点编号,即f(i,j)

完整代码

(详解在注释里)

#include <bits/stdc++.h>
#define ll long long

using namespace std;

const int maxn=1e6+10;
int n,m,r,ecnt;
int head[maxn],depth[maxn],f[maxn][30];//这个30根据最大深度而来如果给出n个结点那么2^k=n  k=log2 n 所以得出30
//链式前向星存图
struct edge
{
    int u,v,next;
} E[maxn];
//添加边
void add(int u,int v)
{
    E[++ecnt].u=u;
    E[ecnt].v=v;
    E[ecnt].next=head[u];
    head[u]=ecnt;
}

void dfs(int u,int d)
{
    depth[u]=d;//确定每个结点深度
    for(int i=head[u]; i; i=E[i].next)//链式前向星的模板遍历
    {
        int v=E[i].v;
        if(!depth[v])
        {
            dfs(v,d+1);
            f[v][0]=u;//v结点向前走1步为u结点
        }
    }
}

int  LCA(int x,int y)
{
    if(depth[x]<depth[y]) swap(x,y); //假设x为深度最大的点
    //将x和y的深度统一为y的深度 20根据n的大小而来
    for(int i=20; i>=0; i--)
    {
        if(depth[x]-(1<<i)>=depth[y]) //每次向上走 2的i次幂步
        {
            x=f[x][i];
        }
    }
    if(x==y) return x; //如果已经在同一结点那么不需要在向上走了,直接返回x为答案
    //一起向上走
    for(int i=20; i>=0; i--)//从大步-->小步
    {
        if(f[x][i]!=f[y][i]) //只要不在一个结点就向上走
        {
            x=f[x][i];//x移动2^i步
            y=f[y][i];//y移动2^i步
        }//只要不同就一直向上爬2的i次幂,所以当i=0时一定不会执行if此时在上一步一定是最近公共祖先了
    }
    //因为f[x][i]==f[y][i]时一值没有处理,x和y一直没有移动,只有不相等时才移动所以最后差一步为答案,不懂的可以动手模拟一下
    return f[x][0]; //最后在向上走一步为答案

}


int main()
{

    cin>>n>>m>>r;//读入n个结点 m次询问 r为根节点

    int u,v;
    for(int i=1; i<=n-1; i++)
    {
        scanf("%d%d",&u,&v);
        //不要忘记添加双向边
        add(u,v);
        add(v,u);
    }
    f[r][0]=r;//根结点向前走2^k步仍为根节点
    dfs(r,1);//深搜求出每个结点的深度,以及f(i,0)走一步所对应的结点是谁
    //预处理,倍增的核心
    for(int i=1; (1<<i)<=n; i++) //1<<i 为2的i次幂步
    {
        for(int j=1; j<=n; j++)//遍历n个结点,i和j的顺序不要乱
        {
            f[j][i]=f[f[j][i-1]][i-1];
        }
    }
    //m次询问输出结果
    for(int i=1; i<=m; i++)
    {
        scanf("%d%d",&u,&v);
        cout<<LCA(u,v)<<endl;
    }

    return 0;
}

根据最开始的图举例

17 ->10(到达同一深度)->7->3(最后在走一步为答案)
11->等待到达同一深度->5->3

复杂度分析

显然以前需要走n步,现在只需要log2n 步 所以复杂度由O(n)–>O(logn)