最近公共祖先LCA算法

耳朵听不见deaf

于 2025-07-01 19:45:16 发布

阅读量948

点赞数 30

CC 4.0 BY-SA版权

分类专栏： ACM 文章标签：算法

本文链接：https://blog.youkuaiyun.com/lwltql/article/details/149053433

ACM 专栏收录该内容

3 篇文章

订阅专栏

我是菜鸟ACMer（qwq），之前学图论板块的LCA算法做的一些笔记，适合小白，分享出来希望能帮助大家！

文章目录

1.向上标记法
2.倍增法
3.tarjan
4.实战演练
总结
思考题

LCA（Least Common Ancestors），即最近公共祖先，指在一颗有根树 T 的任意两个结点 u 、v ，最近公共祖先 LCA(T, u, v) 表示一个结点 x，满足 x 是 u、v 的祖先且 x 的深度尽可能大、离根尽可能远。

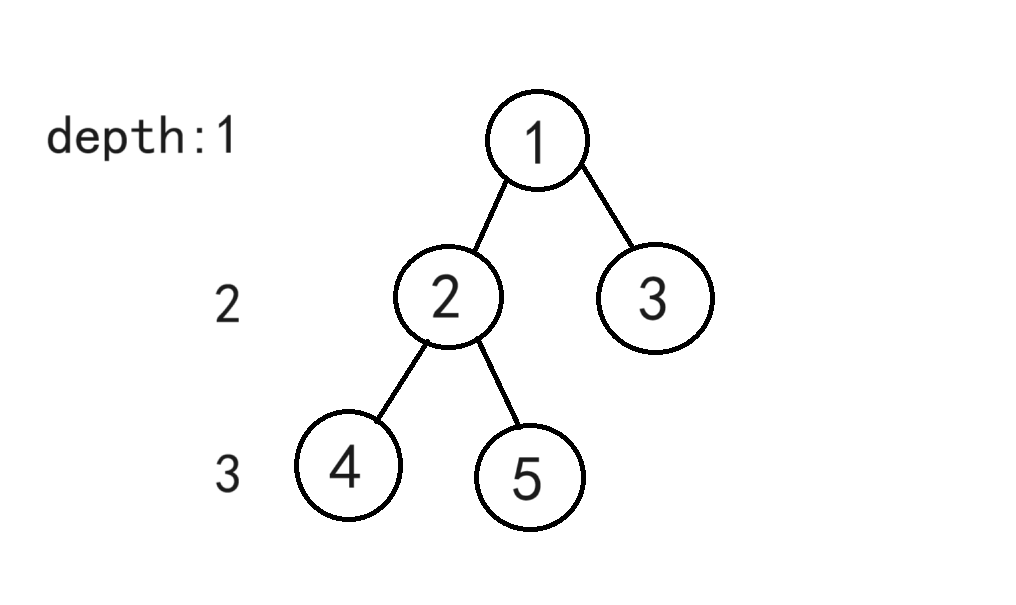
如图，这是一颗有根树，根节点是1，节点4和节点5的公共祖先是节点2和节点1，但是离它们最近（即深度最大、离根最远）的是节点2，所以节点2便是节点4和节点5的最近公共祖先

如何找两个节点的最近公共祖先？以下介绍三种方法

1.向上标记法

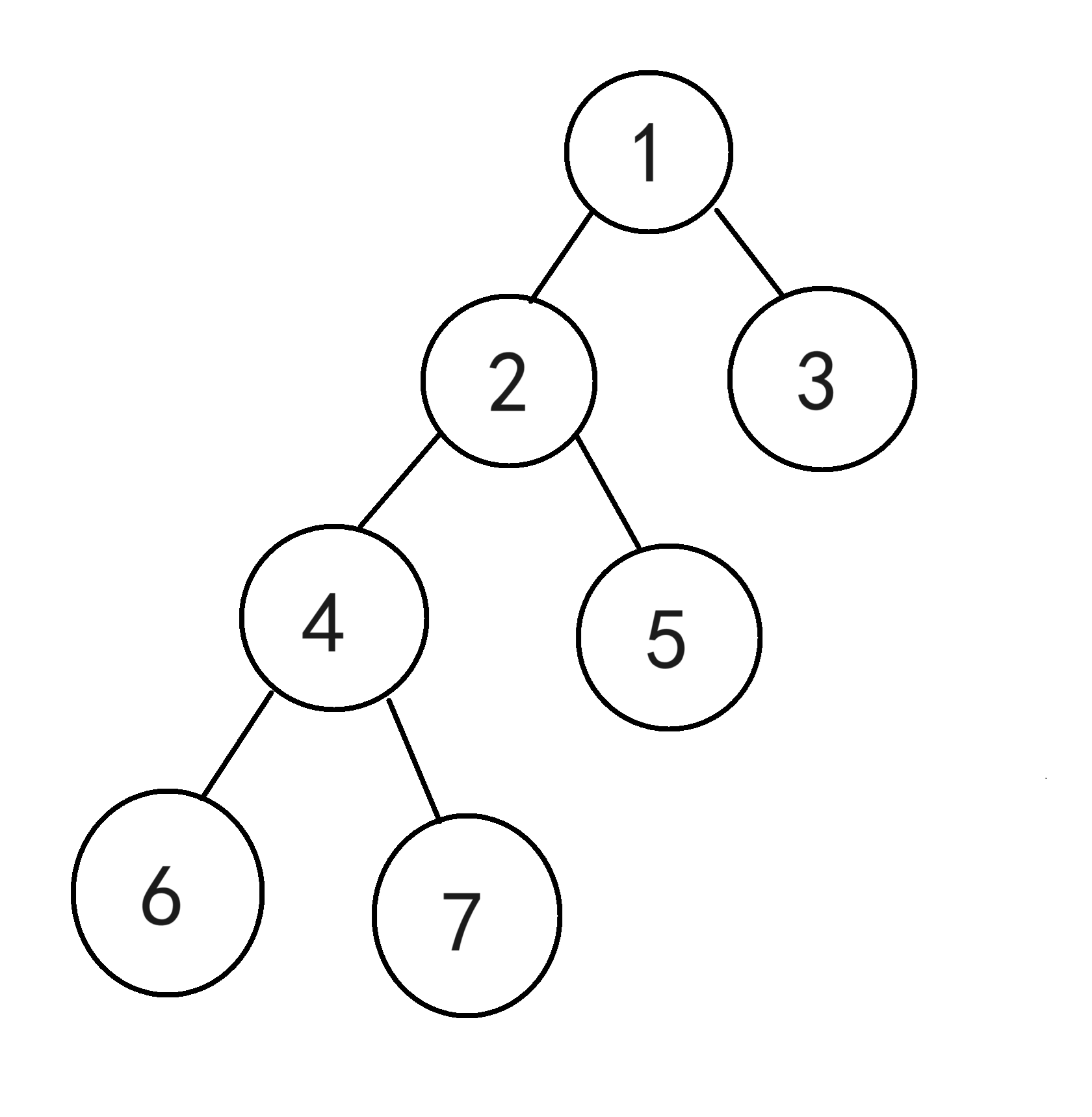
如图，求LCA(5,6)，即找节点5和节点6的最近公共祖先

步骤：

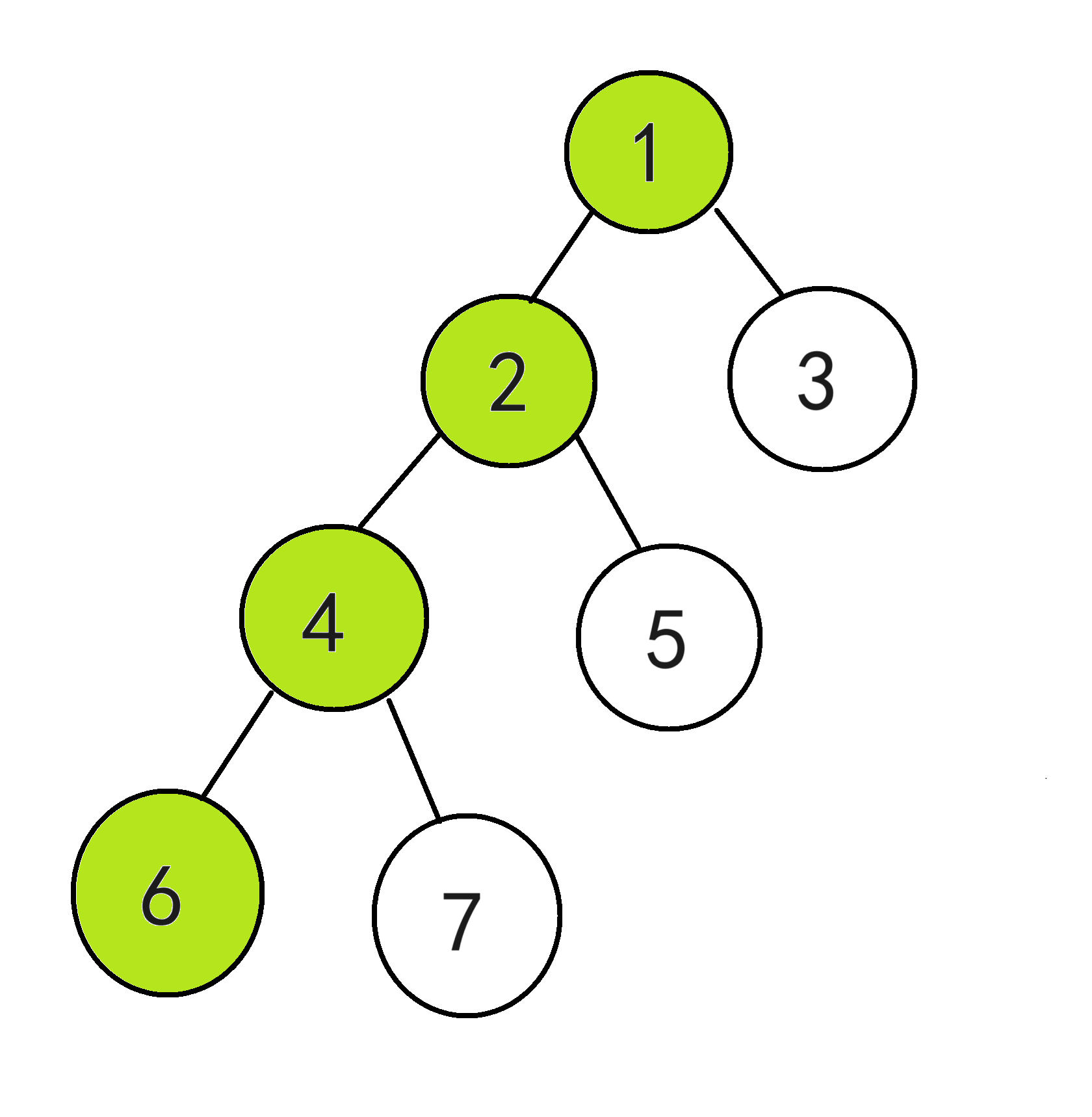
① 先从点6往上爬到根节点,爬过的点都标记绿色

② 再从点5往上爬,碰到的第一个带绿色标记的点就是两者的最近公共祖先

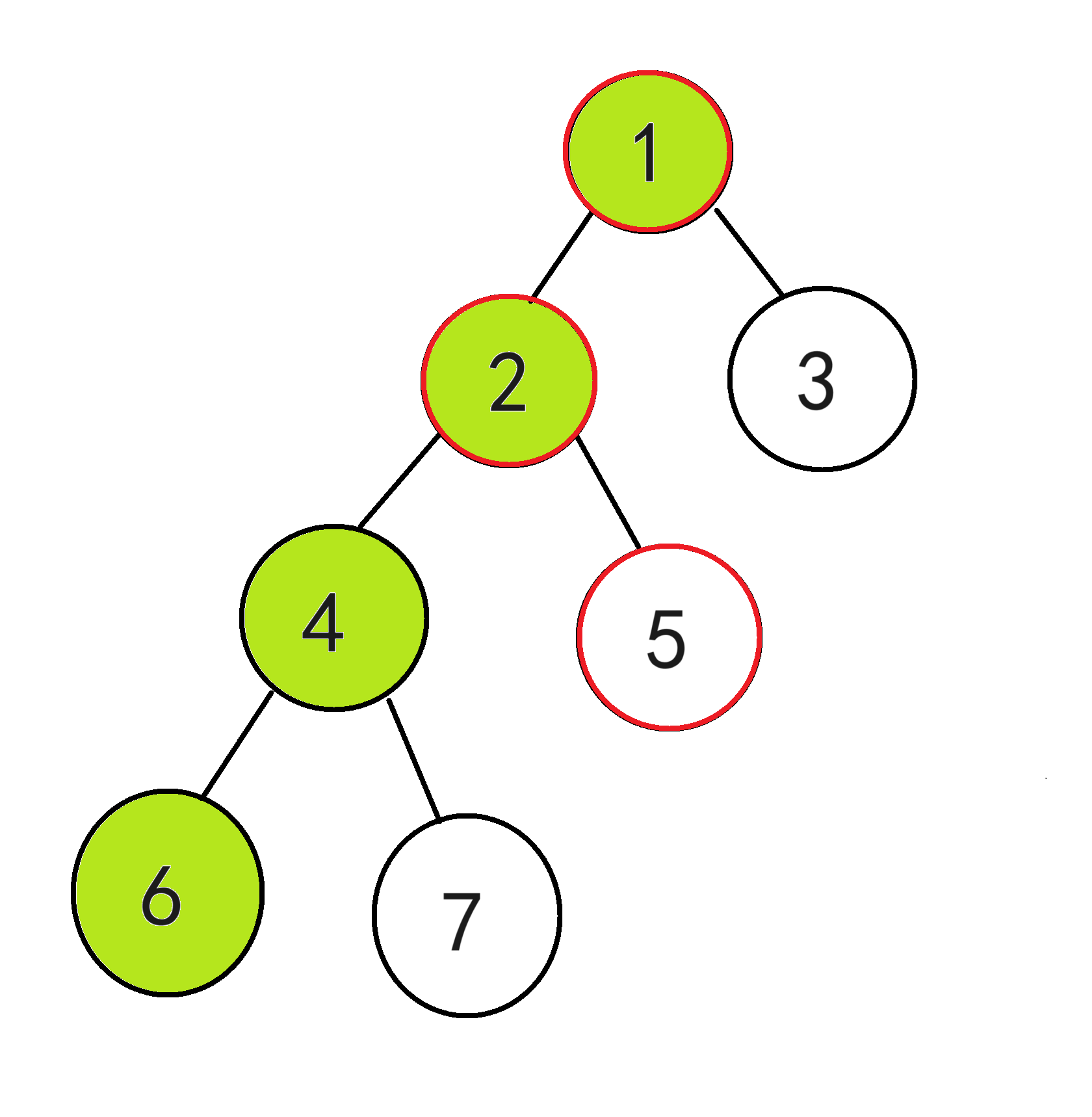
所以LCA（5，6）=2，即点2是点5和点6的最近公共祖先

此方法便是向上标记法，时间复杂度是O(n)，算法步骤简单，是一种暴力方法，很少用

const int N=1e5+10;
int p[N],st[N];
//向上标记法
int LCA(int u,int v)
{
    if(u==v)return u;//相同点，自己是自己的lca
    
    st[u]=1;//先标记u自己，然后u往上爬，爬到根节点
    while(p[u]!=u)//当x=p[x],x便是根节点
    {
        u=p[u];
        st[u]=1;//每爬一次就标记
    }
    
    if(st[v])return v;//v是u的lca
    
    while(p[v]!=v)//v也向上爬
    {
        v=p[v];
        if(st[v])return v;//第一次爬到共同点，共同点便是lca
    }
    
    return 0;//没有lca，节点编号一般从1开始，所以没有节点0，0只是个哨兵
}

2.倍增法

相比于向上标记法一点一点往上爬的慢速，倍增法则是往上倍增跳的快速

介绍倍增法的步骤之前，我们先了解ST表：fa[i][j]表示从节点i开始，向上跳 $2^j$ 层所能到达的节点，即fa[i][j]记录节点i的第 $2^j$ 个祖先节点

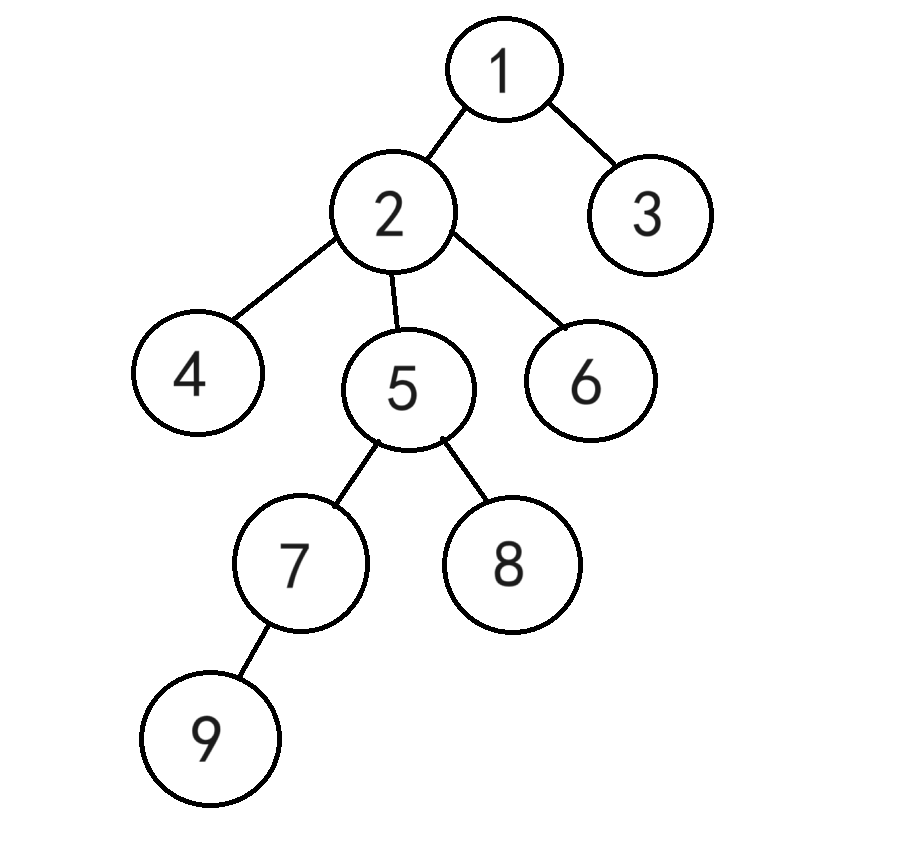
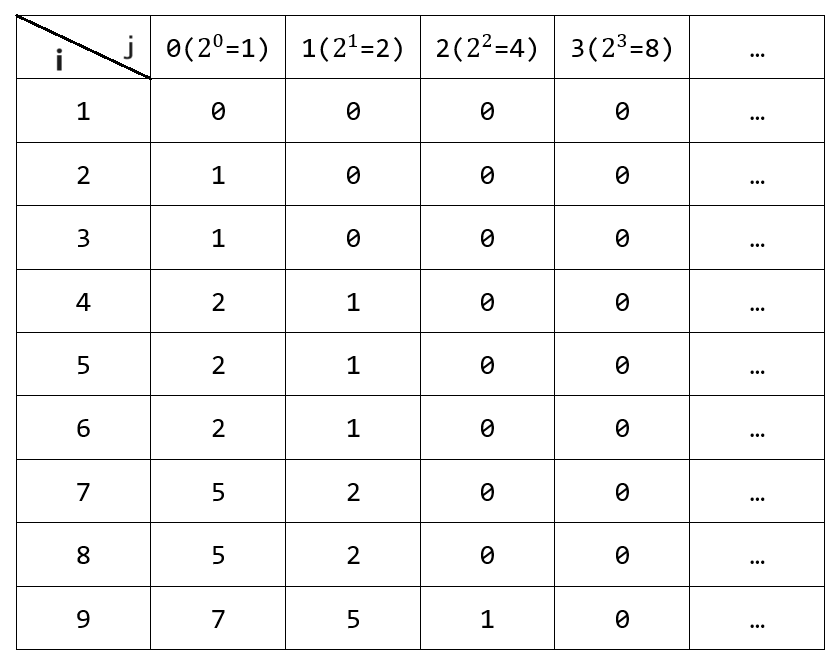
（其中0是个哨兵，节点编号一般都是从1开始，所以不存在节点0，如果跳过根节点之外，那么相应的fa[i][j]标记为0）

如上图中的表格，便是ST表，记录每个节点i（1~9）往上跳 $2^j$ 层祖先。例如，节点9往上跳 $2^0$ 层祖先是7，往上跳 $2^1$ 层祖先是5，往上跳 $2^2$ 层祖先是1，往上跳 $2^3$ 层祖先是哨兵0

如何创建ST表？根据 $2^j$ = $2^{j-1}$ + $2^{j-1}$ 倍增递推的方法可以求出fa[i][j]=fa[fa[i][j-1]][j-1]，如下图

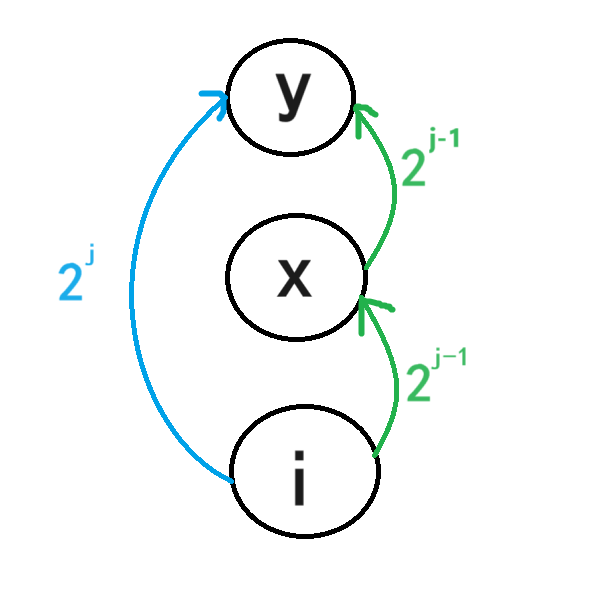
图中的节点i向往上跳 $2^{j-1}$ 层到达节点x，然后节点x往上跳 $2^{j-1}$ 层到达y，即相当于i往上跳 $2^j$ 层到达节点y

可以用dfs或bfs方法预处理打出ST表，从根节点开始入手打表，至上而下，上面的父节点打完，下面子节点通过递推的方式跳到父节点，通过父节点打过的表往上跳，不用再重新打多表，有点记忆化搜索的味道在里面

预处理时间O（nlogn）

dfs递归层数过多容易爆栈，所以以下的代码用的是bfs来打表

const int N = 40010, M = N * 2;

int depth[N], fa[N][16];
//depth[i]记录节点i的深度，方便找lca，同时可以记录该节点是否被搜索过

void bfs(int root)
{
    memset(depth,0x3f,sizeof depth);
    depth[0] = 0,depth[root] = 1;
    
    queue<int> q;
    q.push(root);
    while(q.size())
    {
        int t = q.front();
        q.pop();
        
        for(int i=h[t];i!=-1;i=ne[i])
        //枚举节点t的儿子们
        {
            int j = e[i];
            if(depth[j]>depth[t]+1)
            //说明j还没被搜索过
            {
                depth[j] = depth[t]+1;
                q.push(j);//把儿子j加进队列
                fa[j][0] = t;//j往上跳2^0步后就是父节点t
                for(int k=1;k<=15;k++)
                //k的最大范围取决于题目的节点编号，2^15=32768
                {
                    fa[j][k] = fa[fa[j][k-1]][k-1];//倍增递推
                }
            }
        }
    }

了解完ST表后，我们才来了解倍增法。

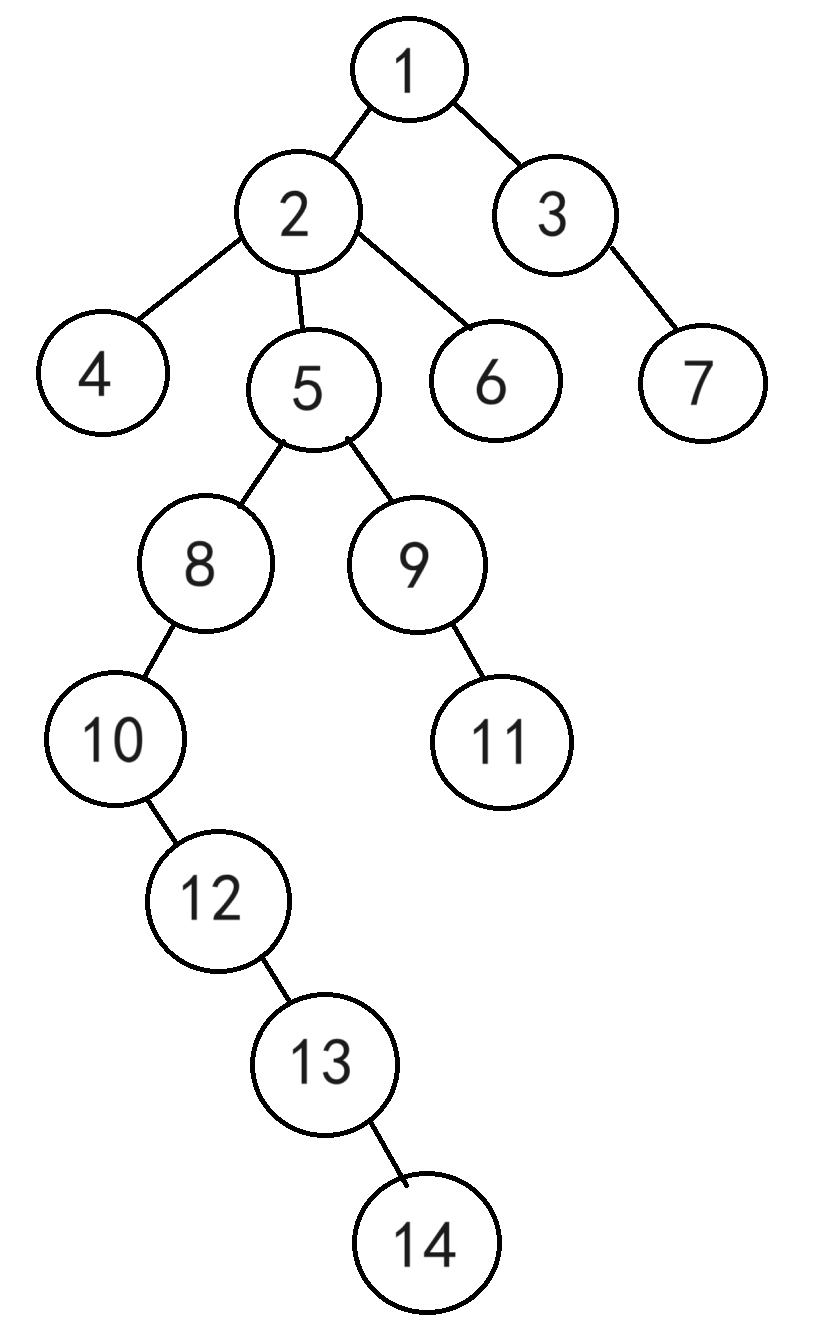
如图，求LCA（7，14）

① 将两个点跳到同一层。深度小的不动，深度大的点往上跳，跳到同一层为止

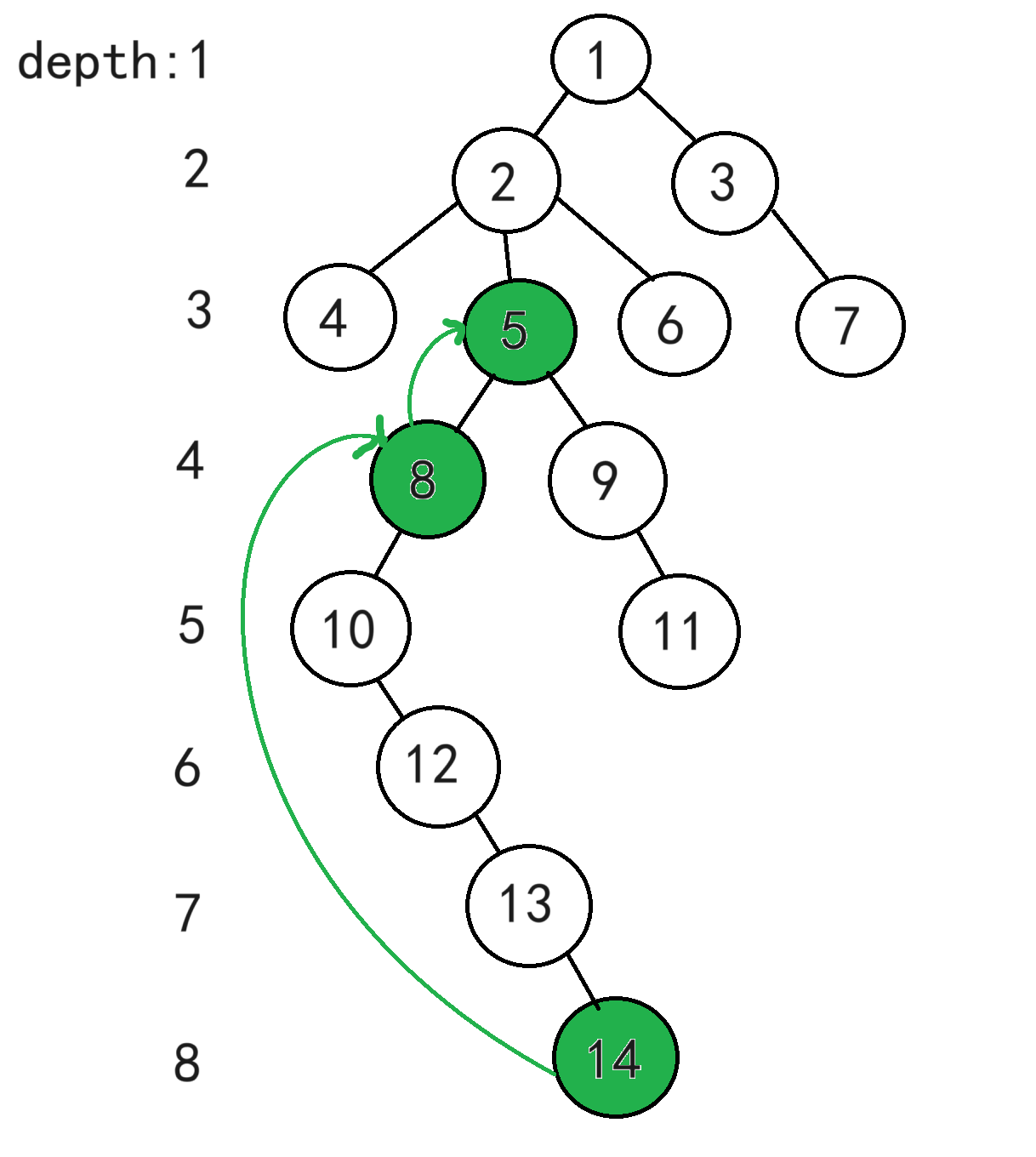
不管怎么跳，都跳不到同一层吗？根据"任意整数可以表示成若干个2的次幂项的和" 这一性质（二进制拼凑法），所以总能跳到同一层的。例如节点14的深度为8，要跳到深度为3，总共跳5层，5= $2^2$ + $2^0$ 。所以节点14先往上跳4层到达节点8，节点8再往上跳1层到达节点5。至于跳多少层到达哪个节点用的就是上面所说的ST表。

② 让两个点同时往上跳，一直跳到两点的最近公共祖先的下一层

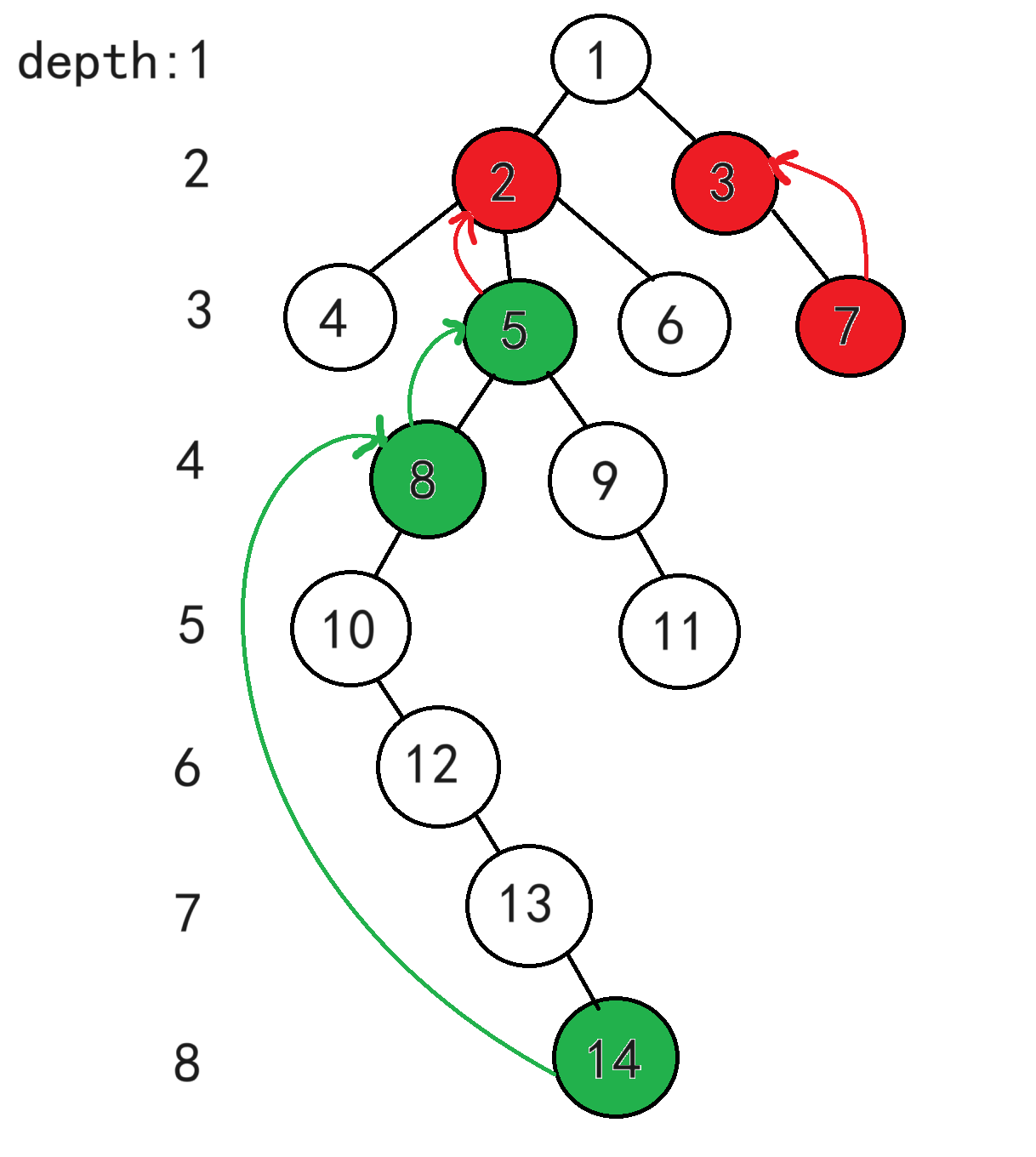
为什么要跳到lca的下一层，而不是直接跳到lca？因为两点的公共祖先有很多个，但我们要找的是最近公共祖先，容易误认我们找到的节点就是最近公共祖先，但其实我们找到的可能是公共祖先。为了避免找错，就直接跳到非祖先节点（lca的下一层）即可，再往上跳一层就是lca，所以LCA（7，14）=1

查询时间是O（logn），对比向上标记法O(n)大大加快了效率

int lca(int a, int b)
{
    
    if (depth[a] < depth[b])
        swap(a, b); //为方便处理，a在下面，b在上面
        
    //下面的a往上跳到b同一层
    for (int k = 15; k >= 0; k -- )
        if (depth[fa[a][k]] >= depth[b])
            a = fa[a][k];
        //当a第一次跳完2^k在b下面，就进入该点，继续跳，直至同一层
        //二进制拼凑法，总会跳到同一层的    
    
    if (a == b) return a;//如果刚好a跳到了点b，b就是lca
    
    //a,b同层但不同节点
    for (int k = 15; k >= 0; k -- )
        if (fa[a][k] != fa[b][k])
        {
            a = fa[a][k];
            b = fa[b][k];
        }
    //循环结束，到达lca下一层，lca(a,b) = 再往上跳1步即可
    return fa[a][0];
}

3.tarjan

对比倍增法是一种在线做法，tarjan算法是一种离线做法，本质上是使用并查集对向上标记法的优化

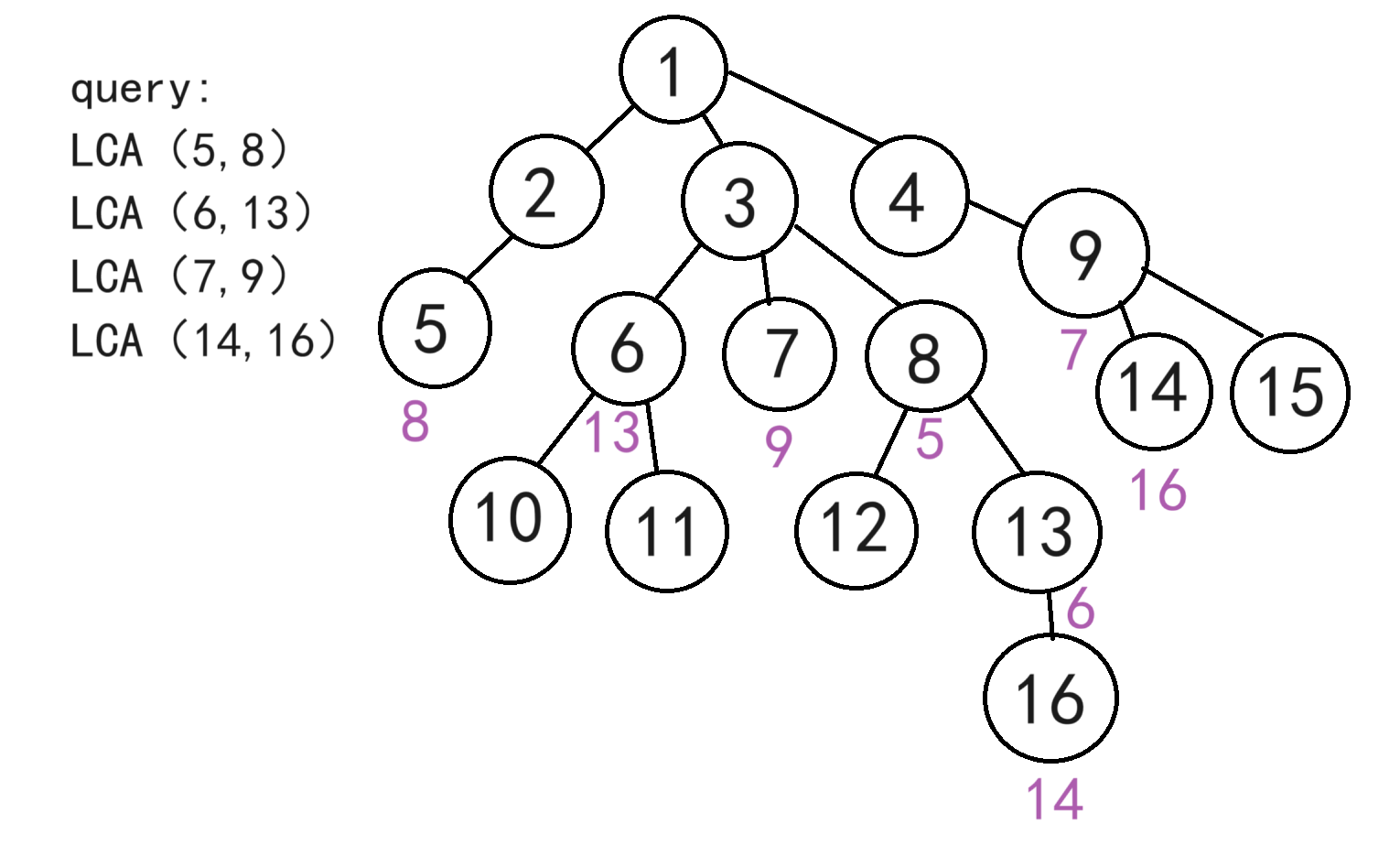
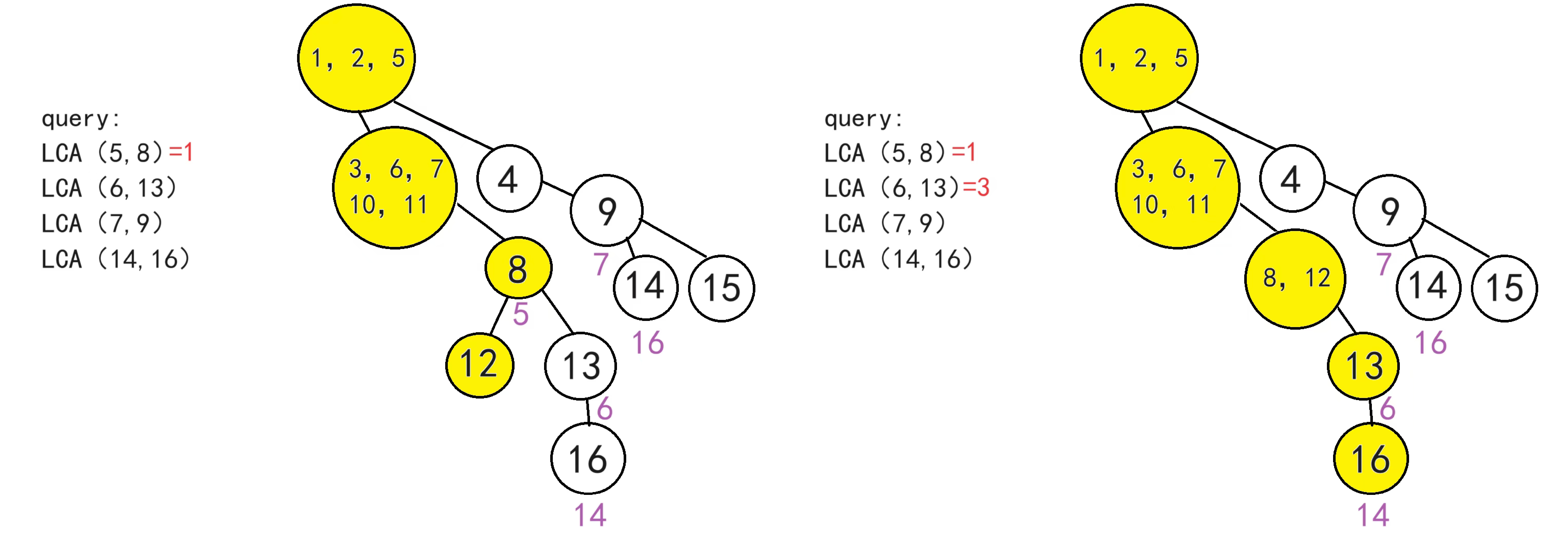
如图，给出一堆查询，求出LCA（5,8），LCA（6,13），LCA（7,9），LCA（14,16）

① 先将所有询问存储下来。将所有查询分别存储到对应的节点下方，实际上将所有查询复制了一份分别存储在两个节点的下方。

typedef pair<int, int> PII;
vector<PII> query[N];
// query[i],i存查询的第一个点，first存查询的另外一个点，second存查询编号（即第几组查询）
void queries()
{
    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        cin>>a>>b;
        if (a != b)
        {
            query[a].push_back({b, i});
            query[b].push_back({a, i});
        }
    }
}

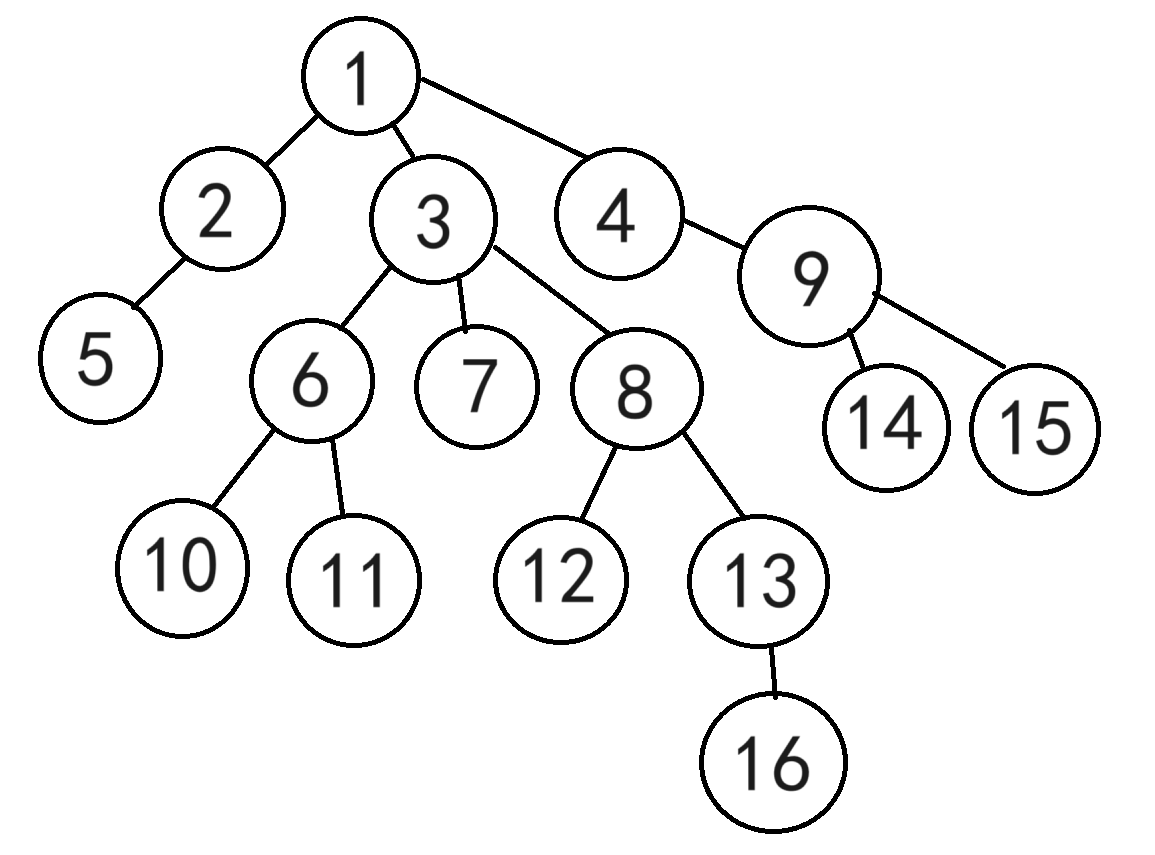
② 在dfs中离线处理求lca。dfs采用类似先续遍历的方式，在dfs时,将所有点分成三大类:

1.已经遍历过,且回溯过的点，标记为2。

2.正在搜索的分支，标记为1。

3.还未搜索到的点，不标记，默认为0

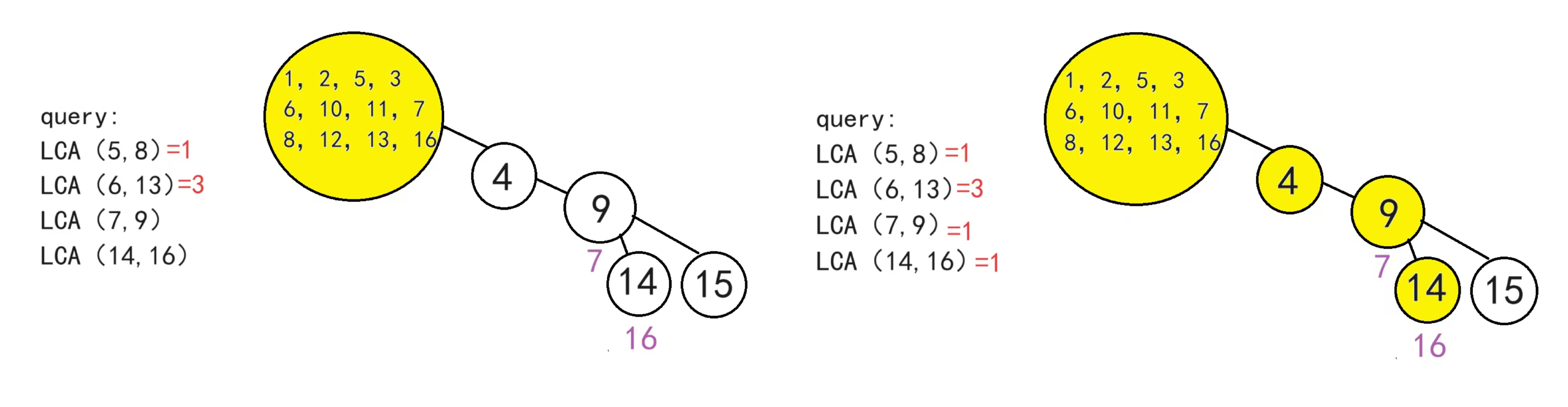
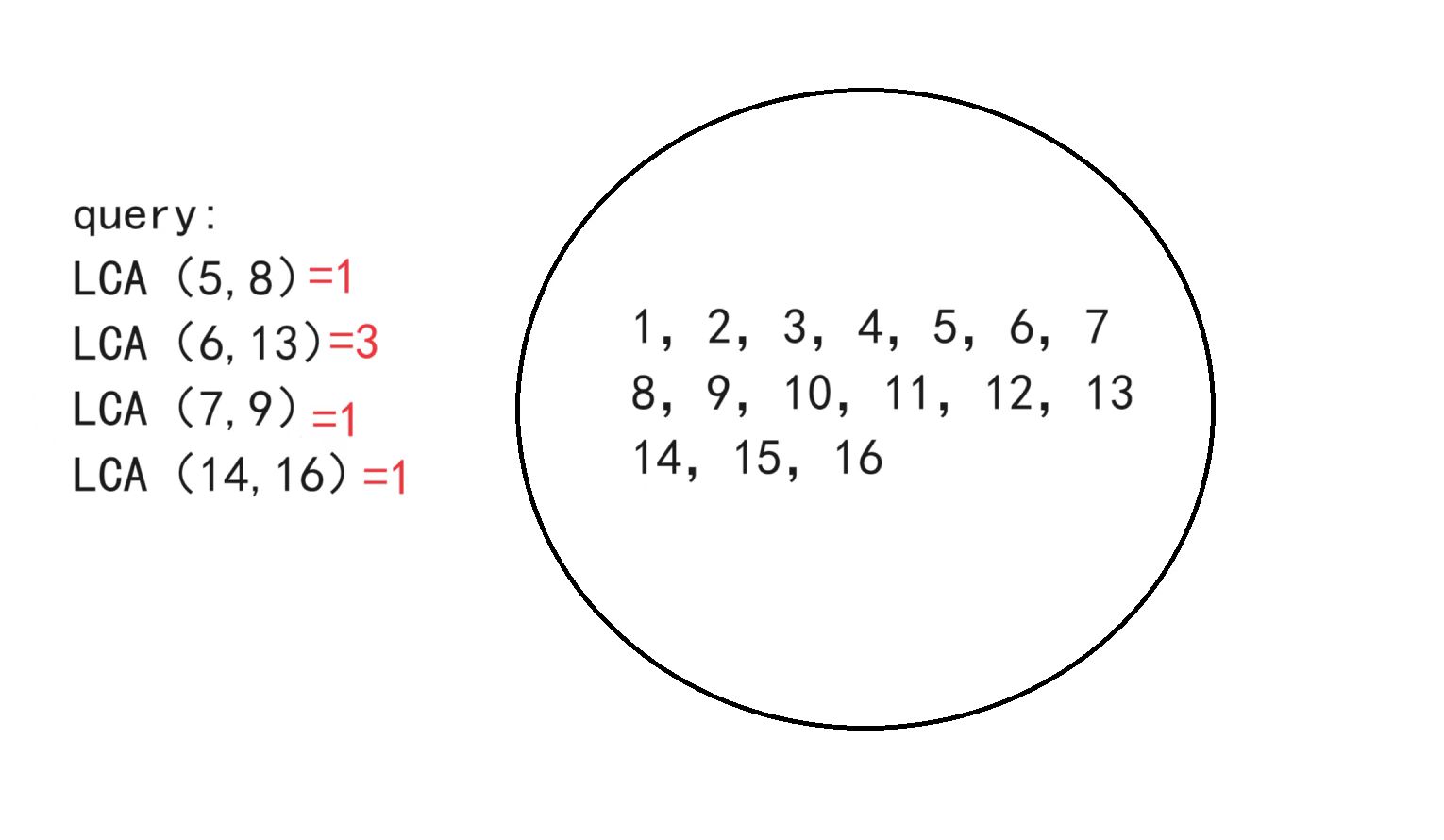
在回溯过的的点中，将子节点合并到父节点，而正在搜索未回溯，tarjan算法会试图解决正在搜索的点的所有查询请求，但是查询请求的另一个点必须是回溯过的点，才能解决。

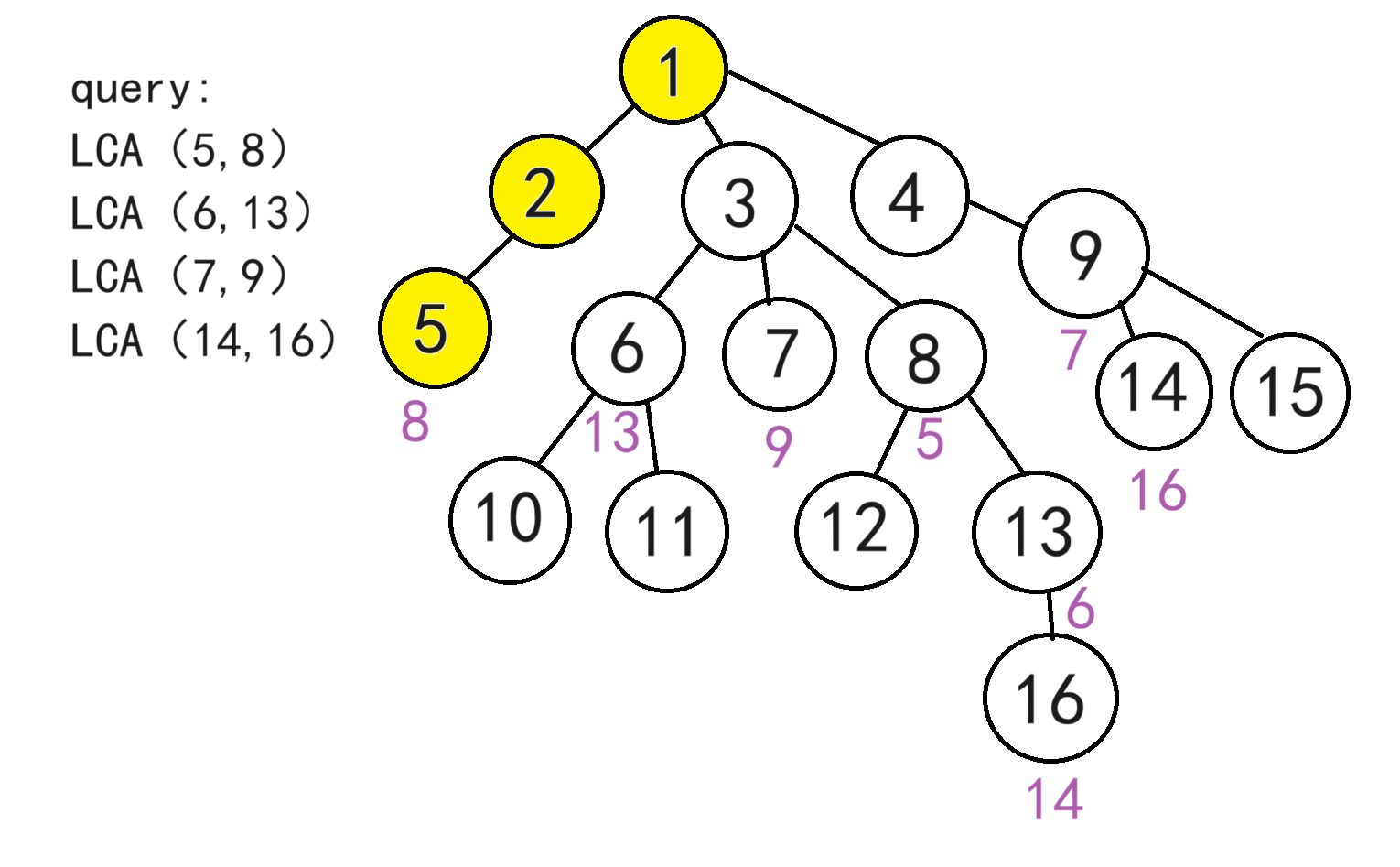
如图，黄色代表正在搜索的点，但是点5对应的点8属于还没搜索过且回溯过，所以暂时无法解决查询请求，只能回溯，回溯过程中，我们将5并入2，2并入1，并查集的路径压缩，最后1、2、5会并在一起

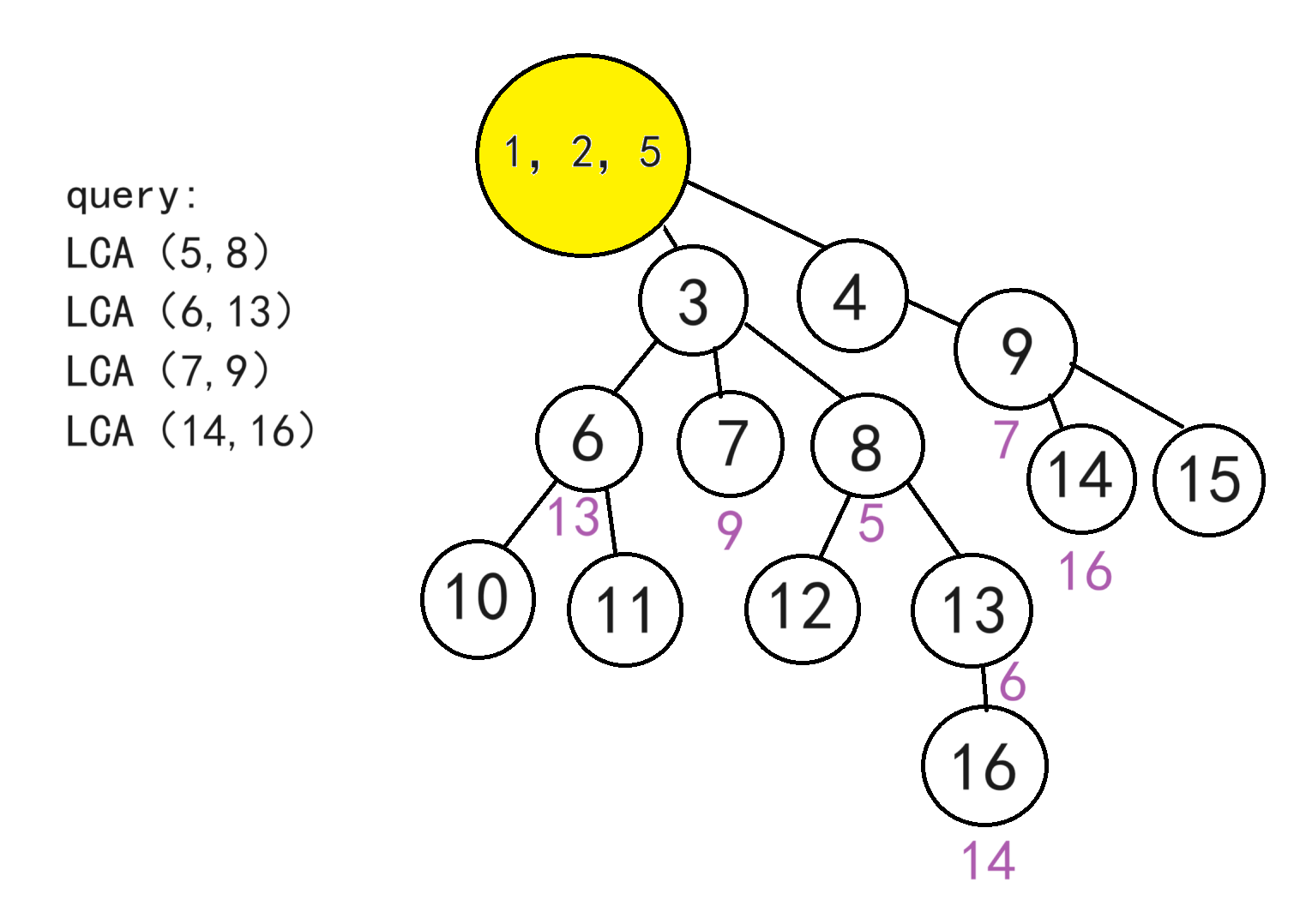
依此类推

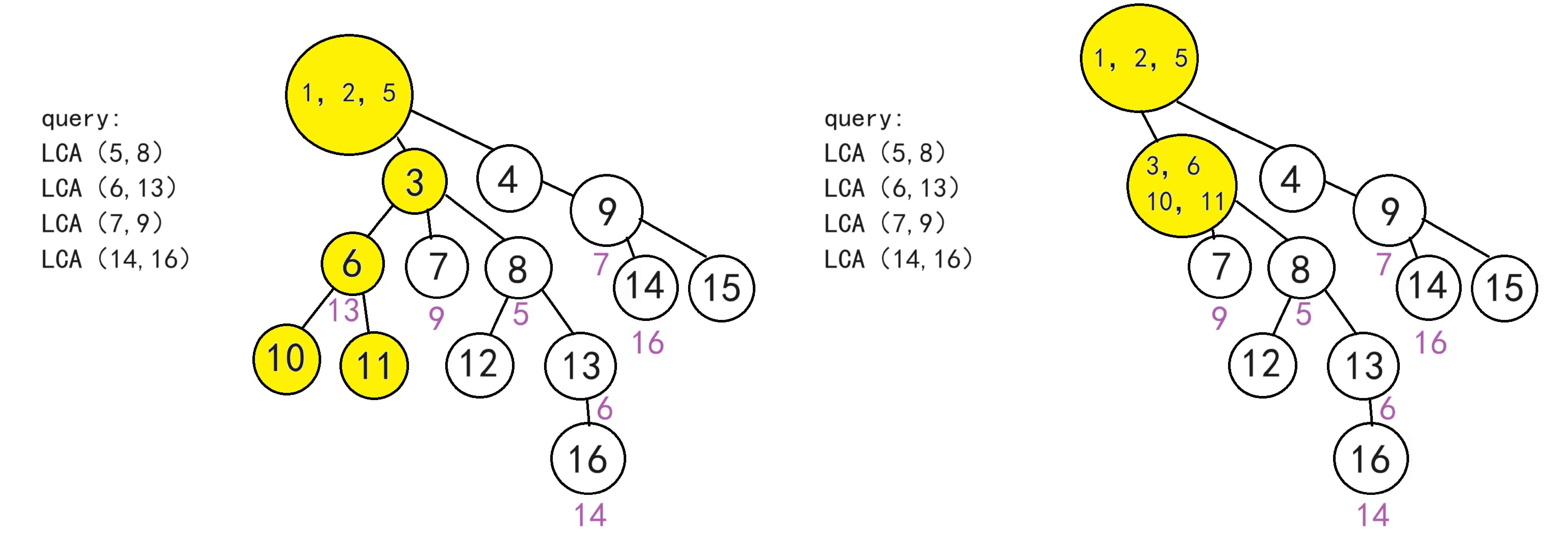
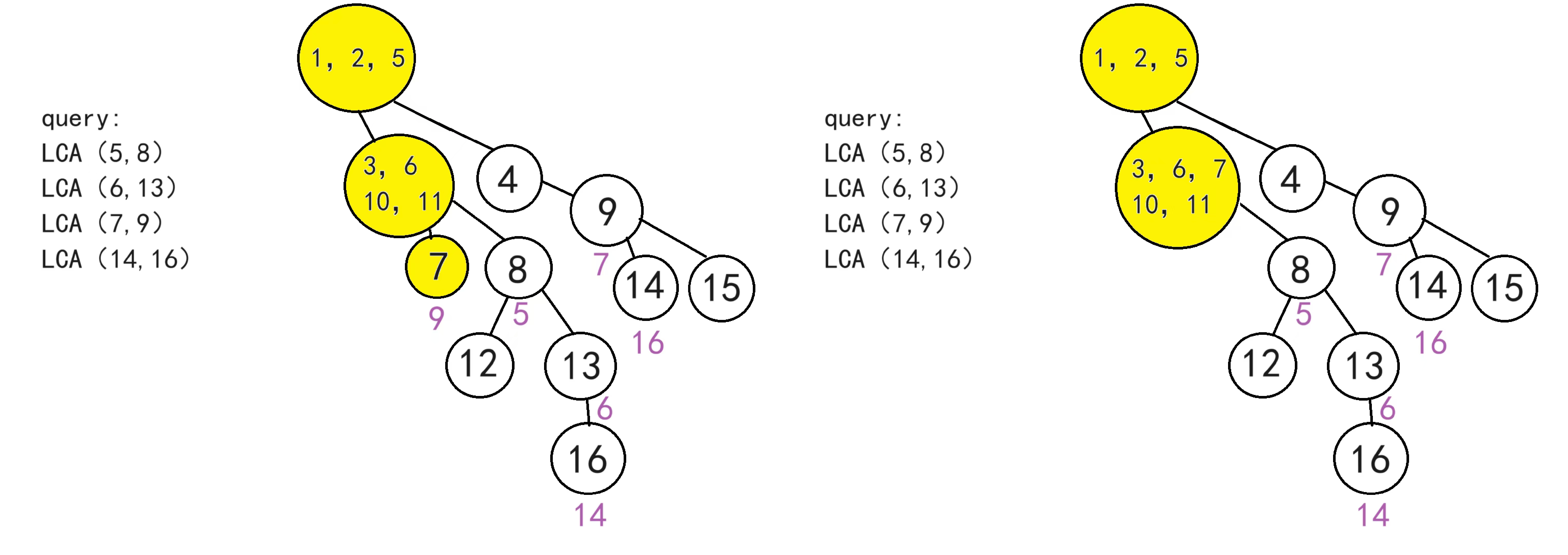
处理时间是O（n），查询时间O（1）


const int N = 10010, M = N * 2;

int p[N];//并查集
int res[M];//存储答案
int st[N];//标记数组

int find(int x)
{
    if (p[x] != x) p[x] = find(p[x]);//路径压缩
    return p[x];
}

void tarjan(int u)
{
    st[u]=1;//当前正在搜索的点标记为1
    for(int i = h[u];~i;i=ne[i])//枚举u的儿子们
    {
        int j = e[i];
        if(!st[j])//若儿子j没搜索过
        {
            tarjan(j);//搜索儿子j
            p[j] = u;//回溯后把儿子j合并到父节点u
        }
    }
    
    
    for(auto item:query[u])// 对于当前点u 搜索所有u的查询
    {
        int y = item.first,id = item.second;
        if(st[y]==2)//如果查询的这个点是已经搜索过且回溯过
        {
            res[id] = find(y)//第id组查询的结果
        }
    }
    
    
    st[u] = 2;//点u已经搜索完且要回溯了 就标记为2 
}

Q1:什么是在线做法和离线做法？

顾名思义，在线做法就是询问一次，就马上计算，输出答案；而离线做法则全部询问一口气读入，统一计算，最后统一输出。简而言之，在线是走一步做一步的思想，离线是不按照询问数组的顺序处理query的思想。

Q2:什么时候用在线做法，什么时候用离线做法？

对于正常的题目来讲，两种算法其实都可以使用，基本上都是在线的思路。经典的题目如：动态第K大问题，解法有树套树(在线)和整体二分/CDQ分治(离线)。在线做法的思路相对简单，而代码量大，容易爆栈，离线做法的思路相对复杂，而代码量小，能够利用所有查询的信息来优化处理过程，特别适合于处理大量相似的查询或需要全局优化的场景。常见的在线算法：带有"可持久化"字样的(主席树、可持久化线段树、可持久化字典树等等)，常见的离线算法：整体二分、CDQ分治、莫队算法等。

Q3:Tarjan算法为什么要离线处理，而倍增法要在线处理？

由于tarjan算法其基于dfs遍历和并查集，要是对每个询问都进行单独的dfs遍历，就会跟向上标记法一样耗时爆栈，且tarjan算法运用了并查集进行优化，会压缩路径，若是在线处理的话，要是刚好问到父子关系的两点，这两点已经被合并到最上面的祖宗节点，输出答案便可能不是最近公共祖先，而是公共祖先。所以tarjan算法应该把所用询问统一记下来，dfs一次就行，在遍历树的过程中同时处理所有询问，因此适合采用离线做法。至于倍增法，其预处理过程与询问无关，用离线处理求lca的话跟在线处理没区别，因此没必要多此一举，直接采用在线处理。

4.实战演练

题源：河南萌新联赛（4）2024 第（四）场：河南理工大学 J 尖塔第四强的高手

分析：

（1）题目给的数列是斐波那契数列，预处理打表出斐波那契数列。斐波那契数列增长很快，到了F[25]=121393，超过了n的范围，所以生成的点集最多24个点。用输入的x和k写个for循环便能得出生成的点集。

(2)题意中的"对于其中任意一棵子树，该子树的根节点可以到达该子树内任意一点（包括子树根节点自己）""机宝想找一个结点，使得该结点能到达点集中任意一点，并且在所有符合要求的结点中，该结点距离根节点最远。"显然是找生成点集中所有点的最近公共祖先，因为只有最近公共祖先能达到生成点集中的所有点且离根节点最远。LCA（x1,x2,x3,…）=LCA（LCA（x1,x2）,x3,…）,可以用倍增法先找出两个点的最近公共祖先，再用这个最近公共祖先与下一个点求出最近公共祖先，依此类推，最多求23次

时间复杂度是O（23qlogn）

代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long

const int N=200010,M=N*2;
int h[N],ne[M],e[M],idx;//邻接表套装
int depth[N],fa[N][30];//lca倍增法
int fibo[30];//斐波那契数列
int n,r,q,u,v;

void add(int a,int b)//邻接表建树
{
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
void bfs()//bfs打表
{
    memset(depth,0x3f,sizeof depth);
    queue<int> q;
    q.push(r);
    depth[r]=1,depth[0]=0;
    while(q.size())
    {
        int t=q.front();
        q.pop();

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(depth[j]>depth[t]+1)
            {
                depth[j]=depth[t]+1;
                q.push(j);
                fa[j][0]=t;
                for(int k=1;k<=25;k++)
                    fa[j][k]=fa[fa[j][k-1]][k-1];
            }
        }
    }
}
int lca(int a,int b)//找a与b最近公共祖先
{
    if(depth[a]<depth[b])
        swap(a,b);
    for(int k=25;k>=0;k--)
        if(depth[fa[a][k]]>=depth[b])
            a=fa[a][k];
    if(a==b)
        return a;

    for(int k=25;k>=0;k--)
        if(fa[a][k]!=fa[b][k])
        {
            a=fa[a][k];
            b=fa[b][k];
        }
    return fa[a][0];
}
signed main()
{
    //初始化
    memset(h,-1,sizeof h);
    fibo[1]=1;
    fibo[2]=2;
    for(int i=3;i<=25;i++)//斐波那契数列第25项超过100000
    {
        fibo[i]=fibo[i-1]+fibo[i-2];
    }
    cin>>n>>r>>q;
    for(int i=0;i<n-1;i++)
    {
        cin>>u>>v;
        add(u,v);
        add(v,u);
    }
    bfs();
    for(int i=0;i<q;i++)
    {
        int x,k;
        cin>>x>>k;

        if(k>=25)//k超出25就超出n的范围
            cout<<0<<endl;
        else
        {
            int node1=x+fibo[k];
            if(node1>n)
            {
                cout<<0<<endl;
                continue;
            }
            for(int i=k+1;x+fibo[i]<=n;i++)
            {
                int node2=x+fibo[i];
                node1=lca(node1,node2);
            }
            cout<<node1<<endl;
        }
    }

}