李宏毅机器学习（2017版）_P14：反向传播

相关资料

开源内容：https://linklearner.com/datawhale-homepage/index.html#/learn/detail/13

开源内容：https://github.com/datawhalechina/leeml-notes

开源内容：https://gitee.com/datawhalechina/leeml-notes

视频地址：https://www.bilibili.com/video/BV1Ht411g7Ef

官方地址：http://speech.ee.ntu.edu.tw/~tlkagk/courses.html

参考笔记地址：https://datawhalechina.github.io/leeml-notes/#/chapter14/chapter14

1、梯度下降Gradient Descent

• 给到 $\theta$ (weight and bias)
• 先选择一个初始的 ${\theta }^0$，计算 ${\theta }^0$的损失函数（Loss Function）设一个参数的偏微分
• 计算完这个向量（vector）偏微分，然后就可以去更新 $\theta$
• 百万级别的参数（millions of parameters）

反向传播（Backpropagation）是一个比较有效率的算法，计算梯度（Gradient）的向量（Vector）时，可以有效率的计算出来

2、链式法则（一元及多元）

多元函数链式法则，需要多各个内函数分别做链式法则求偏导并且求和，如上图Case 2。

3、反向传播

3.1、损失函数计算

神经网络（模型）结构如下：计算$y_1$，$y_2$对于参数$w_1$，$w_2$的偏导。

损失函数为各单个数据损失函数的求和：

3.2、梯度（偏导）计算

采用链式法则，进行参数分离：
$$\frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial l}{\partial z}$$
其中$\frac{\partial z}{\partial w}$为前向传播，结果为输入数据$x$；

$\frac{\partial l}{\partial z}$为后向传播，需要再分割不同参数进行计算：
取出一个Neuron进行分析：

引入激活函数$a$，同时明确后续神经元$z^{\prime }$，$z^{\prime \prime }$进行链式法则求导：
$$\frac{\partial l}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial l}{\partial a}\Rightarrow {\sigma }^{\prime }(z)\frac{\partial l}{\partial a}=\frac{\partial z^{\prime }}{\partial a}\frac{\partial l}{\partial z^{\prime }}+\frac{\partial z^{\prime \prime }}{\partial a}\frac{\partial l}{\partial z^{\prime \prime }}$$

将上式在结构图中标粗，如下：

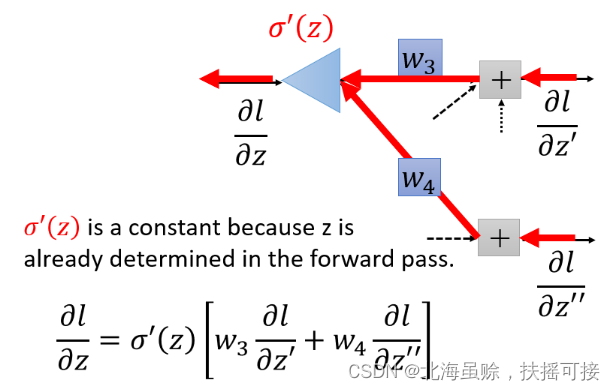
会发现，从另外一个角度看这个事情，现在有另外一个神经元，把forward的过程逆向过来,其中${\sigma }^{\prime }(z)$是常数，因为它在向前传播的时候就已经确定了。

3.3、分输出层讨论

3.3.1、后续为Output layer

假设$\frac{\partial l}{\partial z^{\prime }}$和$\frac{\partial l}{\partial z^{\prime \prime }}$​是最后一层的隐藏层，也就是就是y1与y2是输出值，那么直接计算就能得出$\frac{\partial l}{\partial z}$结果：

3.3.2、后续不为Output layer（即为隐藏层）

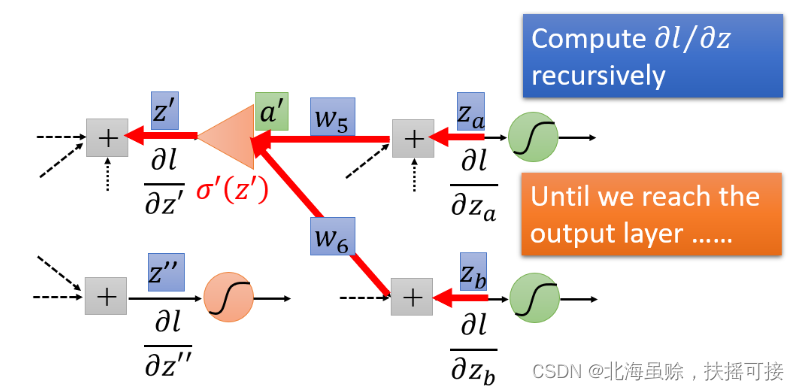
这种情况下，继续计算后面绿色的$\frac{\partial l}{\partial z_a}$和$\frac{\partial l}{\partial z_b}$,然后通过继续乘$w_5$和$w_6$ 得到$\frac{\partial l}{\partial z^{\prime }}$ ，但是要是$\frac{\partial l}{\partial z_a}$和$\frac{\partial l}{\partial z_b}$都不知道，那么我们就继续往后面层计算，一直到碰到输出值，得到输出值之后再反向往输入那个方向走。

实际上进行backward pass时候和向前传播的计算量差不多。

4、总结

$$\frac{\partial l}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial l}{\partial z}$$
我们的目标是要求计算$\frac{\partial z}{\partial w}$（Forward pass的部分）和计算$\frac{\partial l}{\partial z}$ ( Backward pass的部分 )，然后把$\frac{\partial z}{\partial w}$和$\frac{\partial l}{\partial z}$相乘，就可以得到神经网络中所有的参数，然后用梯度下降就可以不断更新，得到损失最小的函数。