李宏毅机器学习（2017版）_P6-8：梯度下降_李宏毅机器学习2017-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_46336048/article/details/125812587

1、梯度下降（Gradient Descent）定义

损失函数最小值求解：
$\theta^{*}=arg \min \min L(\theta)$
$\theta :parameters（参数）$
梯度下降: 在这里插入图片描述
分别计算初始点处，两个参数对 L的偏微分，然后 $\theta^0$ 减掉 $\eta$ (Learning rates（学习速率）)乘上偏微分的值，得到一组新的参数。

2、调整学习率

2.1、恒定学习率问题

在这里插入图片描述
学习率太小（蓝色的线），损失函数下降的非常慢；学习率太大（绿色的线），损失函数下降很快，但马上就卡住不下降了；学习率特别大（黄色的线），损失函数就飞出去了；红色的就是差不多刚好，可以得到一个好的结果。

2.2、自适应学习率（Adaptive Learning Rates）

随着次数的增加，通过一些因子来减少学习率。
刚开始，初始点会距离最低点比较远，使用大一点的学习率，比较靠近最低点了，减小学习率。
例如： $\eta^{t}= \frac{\eta ^{t}}{\sqrt{t+1}}$ ，t是次数。随着次数的增加， $\eta^t$ 减小。
**注意：**学习率不能是一个值通用所有特征，不同的参数需要不同的学习率

3、相关优化算法

3.1、Adagrad 算法

3.1.1、概念

Adagrad算法指每个参数的学习率都把它除上之前微分的均方根。
在这里插入图片描述
公式简化如下：

参数更新过程：

3.1.2、理论解释

对于单变量函数优化：

如果算出来的微分越大，则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比，它可能是比较好的。
梯度越大，就跟最低点的距离越远。

对于多变量函数优化：

最好的迭代步伐是： $\frac{一次微分}{二次微分}$ ，不止和一次微分成正比，还和二次微分成反比。

对于Adagrad算法，分母 $\sqrt{\sum _{i=0}^{t}(g^{i})^{2}}$ 就是希望在尽可能不增加过多运算的情况下模拟二次微分。（如果计算二次微分，在实际情况中可能会增加很多的时间消耗）。

3.2、随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法损失函数不需要处理训练集所有的数据，而是选取一个例子 $x^n$ 处理（每次仅处理一个数据）。不需要像之前那样对所有的数据进行处理，只需要计算某一个例子的损失函数 $L n$ ，就可以更新梯度。
$L=(\widehat{y}^{n}-(b+ \sum _{i}w_{i}x_{i}^{n}))^{2}$ $\theta^{i}= \theta ^{i-1}-n \nabla L^{n}(\theta ^{i-1})$
过程对比如下：
在这里插入图片描述

3.3、特征缩放（Feature Scaling）

3.3.1、概念

某个函数有多个输入特征，并且输入的特征数据分布的范围很不一样，建议把他们的范围缩放，使得不同输入的范围是一样的。 $y=b+w_{1}x_{1}+w_{2}x_{2}$
在这里插入图片描述

3.3.2、原因

$x_1$ 对y的变化影响比较小，所以 $w_1$ 对损失函数的影响比较小， $w_1$ 对损失函数有比较小的微分，所以 $w_1$ 方向上是比较平滑的，同理 $w_2$ 方向较陡峭。
在这里插入图片描述
对于左边的情况，上面讲过这种狭长的情形不用Adagrad的话是比较难处理的。

两个方向上需要不同的学习率，同一组学习率会搞不定它。而右边情形更新参数就会变得比较容易。
左边的梯度下降并不是向着最低点方向走的，而是顺着等高线切线法线方向走的。但绿色就可以向着圆心（最低点）走，这样做参数更新也是比较有效率。

3.3.3、缩放方法

采用批量归一化方法进行缩放，缩放到标准正态分布。
在这里插入图片描述
上图每一列都是一个例子，里面都有一组特征。
对每一个维度i（绿色框）都计算平均数，记做 $m_i$ ；还要计算标准差，记做 $\sigma _i$ 。
然后用第 r(特征)个例子中的第 i（数据）个输入，减掉平均数 $m_i$ ，然后除以标准差 $\sigma _i$ ，得到的结果是所有的维数都是0，所有的方差都是1。（标准正态分布）

4、梯度下降的理论基础

4.1、下降可视化

在这里插入图片描述
在 $\theta^0$ 处，可以在一个小范围的圆圈内找到损失函数细小的 $\theta^1$ ，不断的这样去寻找。
关键在于如果在小圆圈内快速的找到最小值。

4.2、泰勒展开式

4.2.1、单变量泰勒展开式

若 $h (x)$ 在 $x=x_0$ 点的某个领域内有无限阶导数（即无限可微分，infinitely differentiable），那么在此领域内有：
在这里插入图片描述
当x很接近 $x_0$ 时， $h(x)\approx h(x_{0})+h^{\prime}(x_{0})(x-x_{0})$ 。

4.2.2、多变量泰勒展开式

下面是两个变量的泰勒展开式：
在这里插入图片描述

4.3、利用泰勒展开式求解最小值

将损失函数进行泰勒展开，同时略去无穷小项：
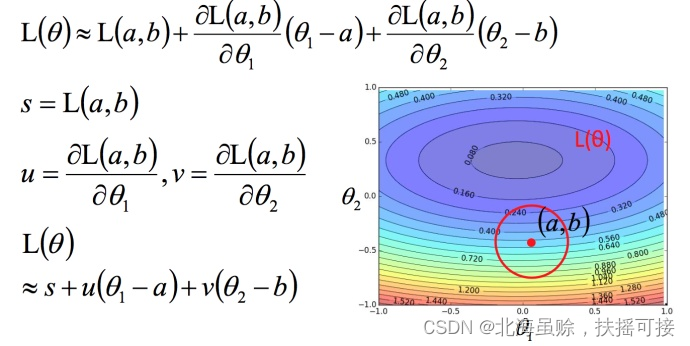
在这里插入图片描述
简化后如下：

利用向量点乘，求出最小值，推导出GD表达式：

注意：上述推导限制条件如下：
**推导前提：**泰勒展开式给的损失函数的估算值是要足够精确的，而这需要红色的圈圈足够小（也就是学习率足够小）来保证。所以理论上每次更新参数都想要损失函数减小的话，